ResNet详细介绍

ResNet的发明者是 何恺明（ Kaiming He）、 张翔宇（ Xiangyu Zhang）、 任少卿（ Shaoqing Ren）和 孙剑（ Jiangxi Sun），取得了2015年ILSVRC 和 COCO比赛 ImageNet classification、ImageNet detection、ImageNet localization、COCO detection、COCO segmentation 的第一名。网络发表在论文《Deep Residual Learning for Image Recognition》，该论文是CVPR2016的最佳论文。

1. 退化问题

---

深度卷积网络在图像分类领域取得了很大的成功，VGGnet和GoogLeNet都通过增加网络深度，获得了很好的性能。

那我们能否简单的通过堆叠网络深度来学习更好的模型呢？

首先，增加网络深度会带来梯度消失和梯度爆炸的问题，但这可以通过归一化初始化和Batch Normalization得到很大程度的解决。

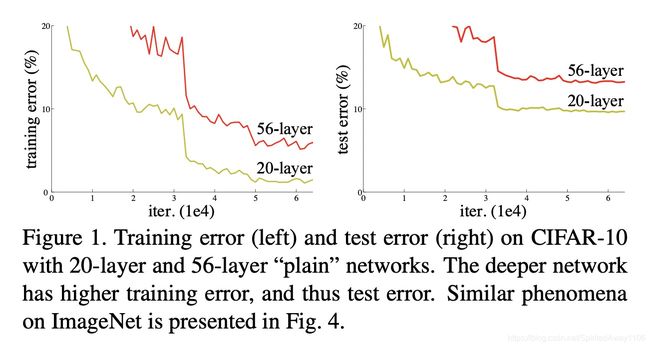
其次，增加网络深度，可能出现退化(degradation)问题，即随着网络深度增加，精度达到饱和，继续增加深度，导致精度快速下降。如下图实验结果

$56$层网络的训练结果和测试结果都要比$20$层的网络差很多，因此也不是过拟合造成的退化。

2. 分析并设计残差块尝试处理退化问题

---

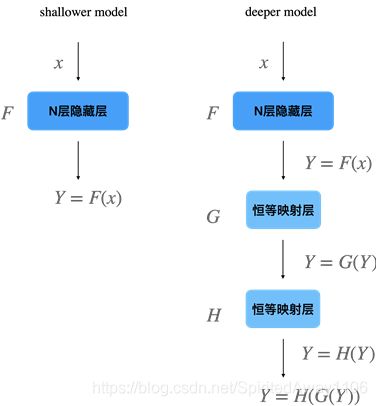
退化问题表明并不是所有的网络模型都能被很简单的优化。作者认为，至少深层的网络不应该比浅层网络表现更差，原因是我们可以设置这样一个网络：在浅层网络中堆叠恒等映射层(identity mapping)来增加网络深度，这些恒等映射层保持输入和输出一致即可。如下图所示：

基于这种方式构建的深层网络，起码能保持浅层网络的训练精度，而不应该得到比浅层网络更高的训练错误率。但是实验结果却出现了退化问题，说明当前的优化方案很难学习这种(带有恒等映射)模型或其他更好的模型。

引发思考，如果让神经网络能够学习恒等映射，也许就能帮助我们解决退化问题，至少能保证深层网络不会比浅层网络的表现更差。

于是作者设计了残差学习模块，假设数据期望的基础映射为$\mathcal{H}(x)$ ，让堆叠的非线性层去拟合残差映射$\mathcal{F}(x)=H(x)-x$，而不是直接拟合$\mathcal{H}(x)$（前面的分析已经知道，当前的优化方案很难学习恒等映射）. 此时基础映射$\mathcal{H}(x)$ 可表示为$\mathcal{F}(x)+x$ 。作者假设优化残差映射比优化原始的基础映射简单，而且如果恒等映射是最优解，将残差映射$\mathcal{F}(x)$置为$0$比通过堆叠一些非线性层来拟合恒等映射更简单。

作者使用下面的网络块来表示 $\mathcal{F}(x)+x$

其中，恒等映射通过“shortcut connections” (上图的弯线连接，指跳过一个或者多个层的连接，后续用跳跃连接表示)实现，如果恒等映射为最优模型，只需要将上图权重层的权重置为$0$即可。 另外，跳跃连接既没有增加参数，也没有增加计算量，且该模型可以使用当前的深度学习工具快速搭建。

其数学表达式为

$$\mathrm{y}=\mathcal{F}(\mathrm{x},\{{\mathrm{W}}_{\mathrm{i}}\})+\mathrm{x}\text{\hspace{1em}(1)}$$

其中$\mathrm{x},\mathrm{y}$分别表示该残差块的输入和输出向量，$\mathcal{F}(\mathrm{x})$是待学习的残差映射，在上图中$$\mathcal{F}(\mathrm{x})={\mathrm{W}}_2\sigma ({\mathrm{W}}_1\mathrm{x})$$ ，其中$\sigma$为激活函数(Relu)，为了方便表示，这里省略了偏置$b$。

由公式$(1)$ 可知，虽然加入了跳跃连接，但是并没有参数和计算复杂度，这点在实验中非常具有吸引力，且我们可以很公平的比较具有相同参数量，深度、宽度和计算成本的普通网络与残差网络。

另外，要求 $\mathrm{x}$与$\mathcal{F}$的维度必须一致，如果不一致(如输入和输出的通道数发生变化)，需要使用线性投影$W_s$来调整$\mathrm{x}$的维度，确保能执行$$y=\mathcal{F}(\mathrm{x},\{{\mathrm{W}}_{\mathrm{i}}\})+{\mathrm{W}}_{\mathrm{s}}\mathrm{x}\text{\hspace{1em}(2)}$$

也可以对公式$(1)$ 使用投影矩阵$W_s$(即对所有的恒等映射都使用线性投影)，但是通过实验对比发现，恒等映射已经足够解决退化问题了，因此只在维度变化时才使用$W_s$.

另外，残差映射$\mathcal{F}$的形式是很灵活的，论文中的$\mathcal{F}$包含两层或者三层权重层，更多层也是可以的 ，但是如果只有一层权重层，此时有$\mathrm{y}={\mathrm{W}}_1\mathrm{x}+\mathrm{x}=({\mathrm{W}}_1+1)\mathrm{x}$，跟不使用残差连接没差别。

3. 通过对比试验，研究残差网络性能

---

作者在$ImageNet$数据集上进行了全面的对比实验，发现

1. 深度残差网络相比普通网络更容易优化
2. 随着网络深度增加，残差网络的性能也会随着提高，并获得了比以前网络好得多的结果

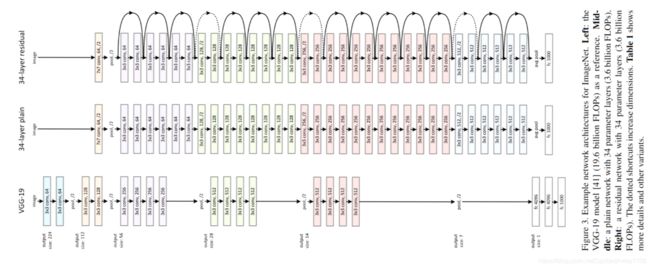
先介绍下普通网络，残差网络以及更深层残差网络的基本结构，如下图所示

• 普通网络(Plain Network)

  普通网络的结构主要受VGG启发，网络结构如上图中"34-layers plain"所对应的网络，有以下特点

  • 卷积主要使用大小为$3\ast 3$的卷积核，如果特征图大小(长和宽)不发生变化，则使用相同数量的卷积核，如果特征图的大小(长和宽)减半，则使用的卷积核数量翻倍，这样能够保持相同的时间复杂度

  • 通过卷积中设置步长为$2$实现下采样

  • 网络最后使用全局平均池化，以及一个具有1000个神经元且使用softmax激活函数的全连接层

• 残差网络(Residual Network)

  基于上图中的普通网络，加入跳跃连接，就构成了残差网络。残差块的配置如下

  • 当残差块的输入和输出维度相同时，使用恒等映射(上图的实线表示的跳跃连接)

  • 如果输出的特征图维度增加(上图虚线表示的跳跃连接)时，则跳跃连接使用两种方式调整输入的特征图通道数

    1. 使用恒等映射，缺少的维度用$0$补齐，这种方式不增加额外的参数

       按照上图的网络结构，特征图通道数发生变化时，其输出的特征图大小(长和宽)也发生了改变(减半)，此时恒等映射如何理解，猜测是将输入特征图沿通道方向以设定步长(论文中是$2$)直接取特征值，作为输出特征图对应通道的特征值，缺少的通道则用全$0$补充(这个不理解也无所谓，后续搭建将使用$1\ast 1$卷积实现跳跃连接的维度调整)，如下图所示

       

    2. 使用$1\ast 1$的卷积调整维度

• 更深层的网络

  除了$34$层的普通和残差网络，还设计了$50$层，$101$层和$152$层的残差网络。对于更深层的网络，为了节约训练时间，在残差块中加入了瓶颈(Bottleneck)设计，如下图右侧图形所示

  

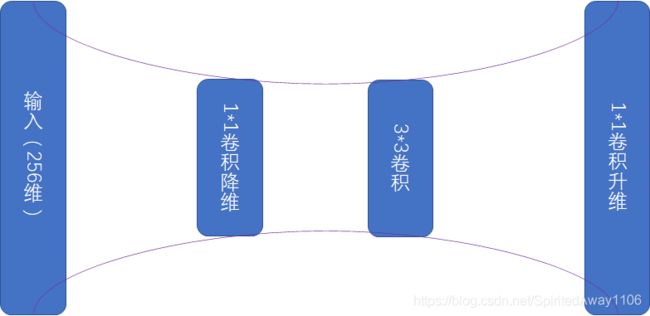
  即在残差映射$\mathcal{F}$中，包含的权重层由两层变为三层。三层权重层分别为$1\ast 1,3\ast 3,1\ast 1$的卷积层，其中$1\ast 1$的卷积用来负责降维和升维，$3\ast 3$的卷积作为低维输入和高维输出的瓶颈

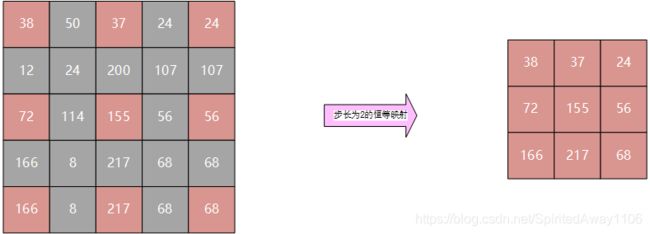
  说一下很无聊的点，为啥$3\ast 3$的卷积叫做瓶颈层，如下图所示，$3\ast 3$卷积核个数决定这个瓶子最细的地方有多细，因此叫做瓶颈层。(图里的维度，表示通道数或卷积核个数)

  

最终，共设计和训练了以下几种网络

• $\left[\begin{array}{c}3\times 3,64\\ 3\times 3,64\end{array}\right]\times 3$ 表示将两层卷积作为一个分组(分组是方便将其转为残差块即$\mathcal{F}$将包含这个分组内的层)，其中第一层卷积使用$64$个大小为$3\times 3$的卷积核，第二层卷积使用$64$个大小为$3\times 3$的卷积核，$\times 3$ 表示具有三个这样的卷积分组。
• FLOPs 表示网络的浮点计算量，观察图表不难发现，当网络加深至$152$层时计算量为$11.3\times 10^9$，约为VGG19计算量 $19.6\times 10^9$的$57.65\%$
• 每次卷积之后，激活之前使用Batch Normalization

4. 实验结果分析

---

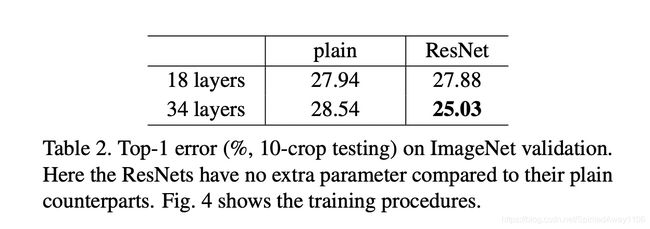
$18$层和$34$层网络的定量结果表如下

训练过程的训练误差和验证集错误率统计图如下

其中粗线条表示验证集错误率，细线表示训练集错误率，通过分析图标，有以下发现：

• 普通网络

  对比了$18$层和$34$层的普通网络(网络结构见上图Table1)，发现$34$层网络的训练和验证集错误率均高于$18$层网络，出现了退化问题，作者认为网络使用了Batch Normalization，并且验证了后向传播时的梯度也处在合理范围，因此排除了梯度消失引起退化的可能性。猜测可能随着网络的加深，网络的收敛速度呈指数下降。

• 残差网络

  对比了$18$层和$34$层的残差网络，网络中的跳跃连接均使用恒等映射，需要增加维度时，使用零填充(zero-padding)，因此和对应的普通网络相比，残差网络没有新增额外的参数

  实验结果发现

  1. $34$层残差网络的训练错误率比$18$层的低，且性能在验证集上得到了很好的泛化，$34$层网络的验证集误差比$18$层的低$2.8\%$ ，说明残差网络很好了解决了退化问题
  2. $34$层残差网络的top-1错误率比$34$层普通网络的错误率低了$3.5\%$ ，精度有很大提升，这表明残差学习对深度网络来说十分有效
  3. $18$层普通网络和残差网络虽然验证集错误率相差无几，但是残差网络收敛更快

  作者还做了实验，用于研究跳跃连接使用恒等映射和投影映射($1\ast 1$卷积调整维度)的差别，首先做了三种跳跃连接的配置

  $(A)$ 使用恒映射， 需要增加维度时，使用零填充(zero-padding)，所有的跳跃连接均不增加参数

  $(B)$ 需要增加维度时，使用投影映射，其他的跳跃连接则使用恒等映射

  $(C)$ 所有的跳跃连接均使用投影映射

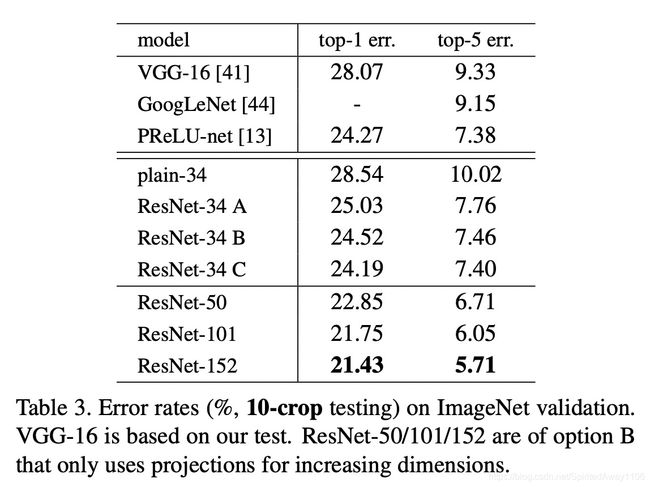
  实验结果如下图

  

  对比发现，$B$比$A$好，原因是使用全零填充的维度学不到东西，$C$比$B$好，认为是引入了更多的参数。但是从整体看$A/B/C$三种配置的错误率差别不大，认为投影映射并不是处理退化问题必须的操作，因此在测试$50/101/152$层残差网络时，跳跃连接使用配置$B$。

  另外，该图表也展示了$50/101/152$层残差网络的结果，发现错误率随着网路加深仍在减小，未发现退化问题。

5. CIFAR-10数据集实验结果分析

---

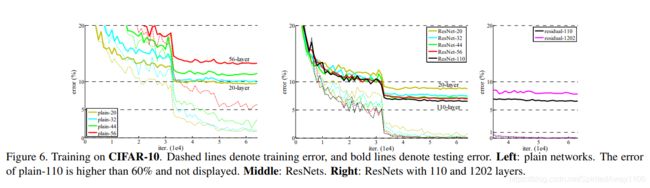
作者利用CIFAR-10数据集也进行了一系列的测试，其测试和训练误差结果图如下图所示(虚线表示训练误差，粗线测试误差)

• 上图左侧图像表示普通网络的训练和测试误差，普通网络随着深度增加，训练误差越来越高，这表明，普通网络随着网络深度增加优化困难的现象(退化问题)是一个普遍的问题

• 上图中间图像为残差网络的训练和测试误差，残差网络随着网络深度的增加训练和测试误差均越来越小，说明残差网络很好的解决了网络深度增加带来的优化困难问题。

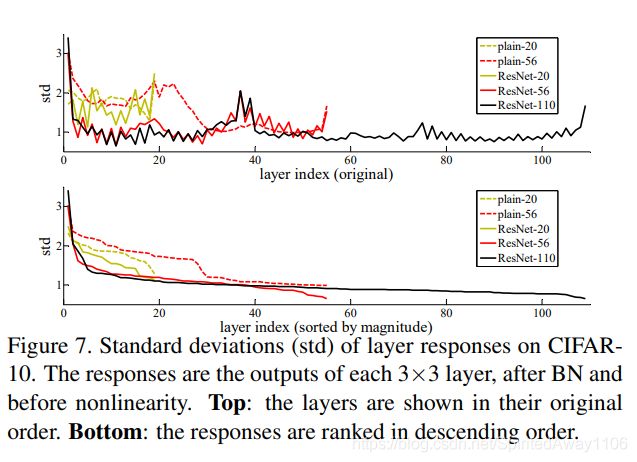
  此外，作者还分析了残差网络的层响应(BN之后、激活函数之前)标准差数据，其结果如下图所示

  

  发现残差函数$\mathcal{F}(x)$比非残差函数更接近$0$，且通过比较$20/56/110$层网络，发现较深的残差网络往往具有更小的数据变动，这跟之前关于残差网络的分析是一致的

• 上图左侧图像为利用残差网络训练更深层($1202$层)网络的结果，发现$1202$层网络比$110$层网络的测试误差低，由于两个网络具有几乎相同的训练误差，因此认为是过拟合造成的，且没有发生退化问题(或者说退化问题不明显)