机器学习2017，Regression（李宏毅

应用举例

 

• 股市预测（Stock market forecast）
  • 输入：过去10年股票的变动、新闻咨询、公司并购咨询等
  • 输出：预测明天道琼斯工业指数的点数
• 自动驾驶（Self-driving Car）
  • 输入：无人车上的各个sensor的数据，红外线感测、视讯镜头看到的等，例如路况、测出的车距等
  • 输出：方向盘的角度
• 商品推荐（Recommendation）
  • 输入：使用者A的特性，商品B的特性
  • 输出：购买商品B的可能性
• Pokemon精灵攻击力预测（Combat Power of a pokemon）：
  • 
  • 输入：进化前的CP值、物种（Bulbasaur）、血量（HP）、重量（Weight）、高度（Height）
  • 输出：进化后的CP值

 

做machine learning三个步骤

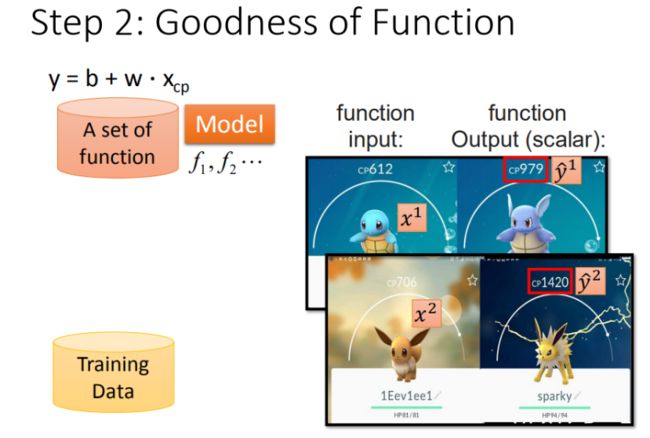
• step1：模型假设，选择模型框架（线性模型）。找一个model（func. set） 
• step2：模型评估，如何判断众多模型的好坏（损失函数）。func. set里面拿一个function出来可以定义好坏
• step3：模型优化，如何筛选最优的模型（梯度下降）。找一个最好的function

多元线性模型（多个特征）

在实际应用中，输入特征肯定不止 x_{cp}xcp​ 这一个。例如，进化前的CP值、物种（Bulbasaur）、血量（HP）、重量（Weight）、高度（Height）等，特征会有很多。

所以我们假设 线性模型 Linear model：y = b + \sum w_ix_iy=b+∑wi​xi​

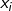• ：就是各种特征(fetrure) ...
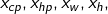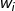• ​：各个特征的权重 ⋅⋅
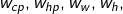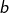• ：偏移量

本例子简化为【单个特征】来示例

Step 2：模型评估 - 损失函数

【单个特征】:

收集和查看训练数据

这里定义 是进化前的CP值，进化后的CP值，真实值

如何判断众多模型的好坏

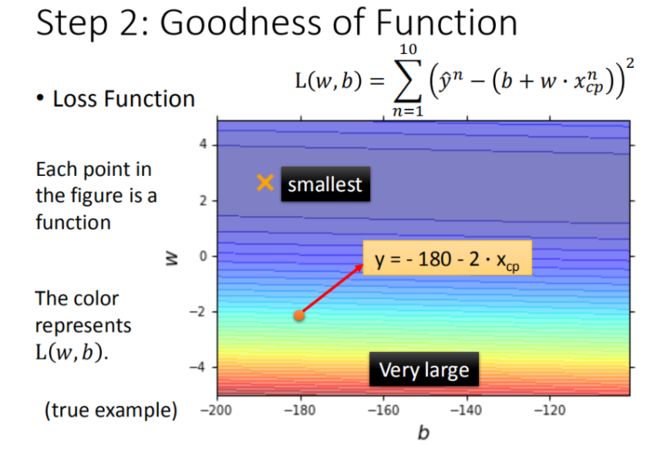
有了这些真实的数据，那我们怎么衡量模型的好坏呢？损失函数（Loss function）

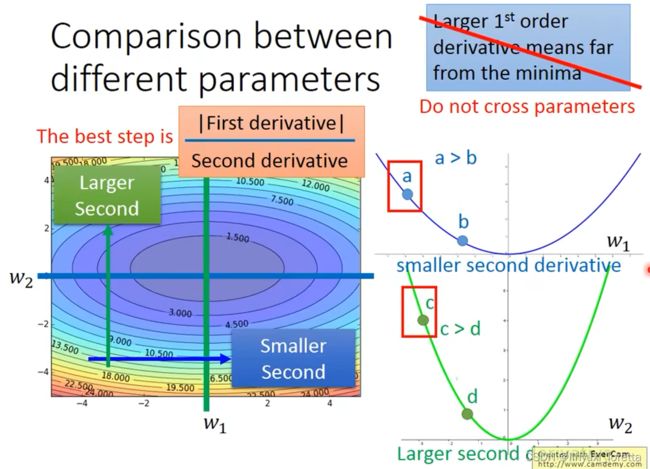
• 图中每一个点代表着一个模型对应的 w 和 b
• 颜色越蓝代表模型更优

可以与后面的图11（等高线）进行对比

Step 3：最佳模型 - 梯度下降

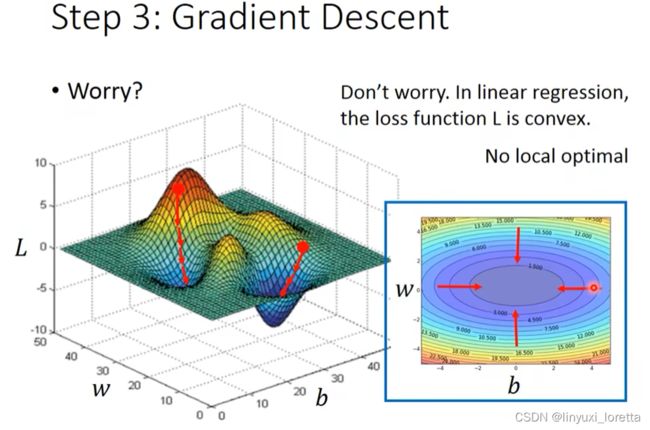
已知损失函数是 L(w,b)，如何筛选最优的模型（参数w，b），梯度下降法

现在的目的，找一个w，让L(w)最小，可以爆搜（穷举）所有w

• 步骤1：随机选取一个 w^0（也有一些方法，日后再讲）
• 步骤2：计算微分，也就是当前的斜率，根据斜率来判定移动的方向
• 步骤3：踏一步的量根据：微分值、学习率 η 
• 重复步骤2和步骤3，直到找到最低点

linear regression没有local minima

梯度下降算法在现实世界中面临的挑战

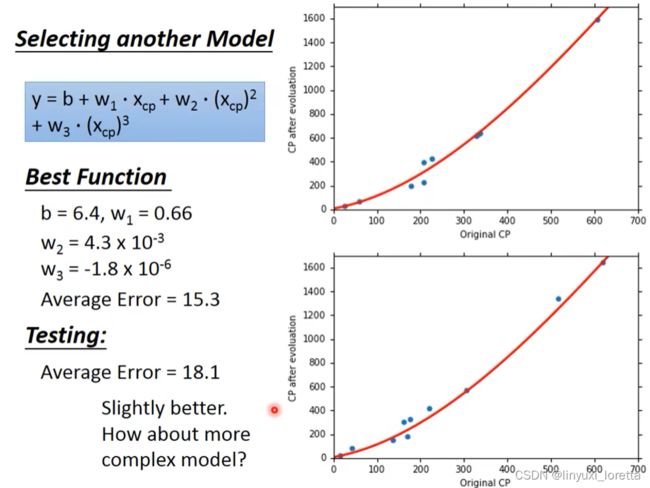
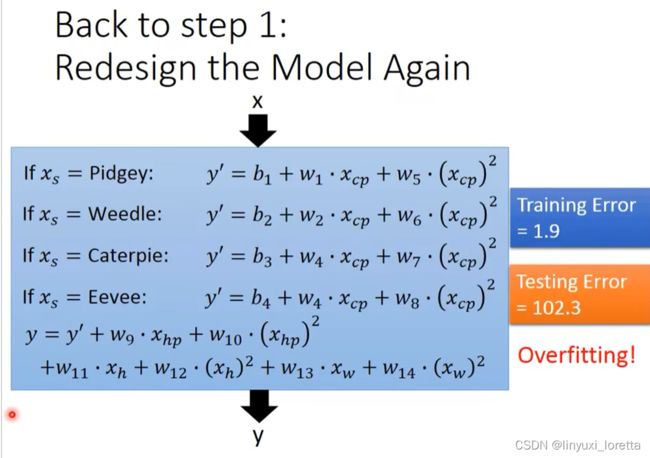
观察data，进化前CP值特别大特别小的时候，预测不太准，---->   重新设计model

 

 

 

 

 

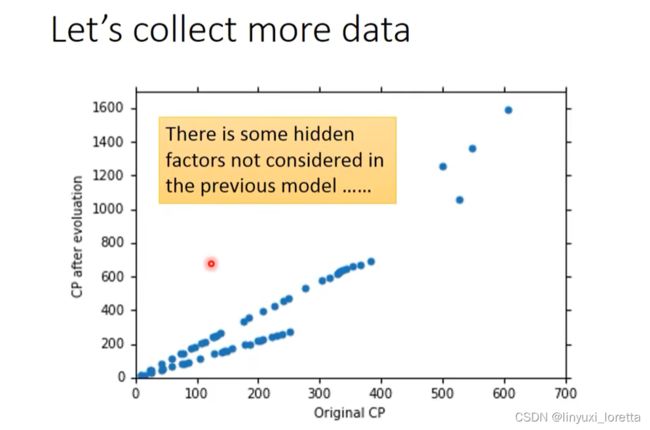
数据从10只扩大到60只，观察data。中间有另外一个力量在影响进化后的数值

步骤优化

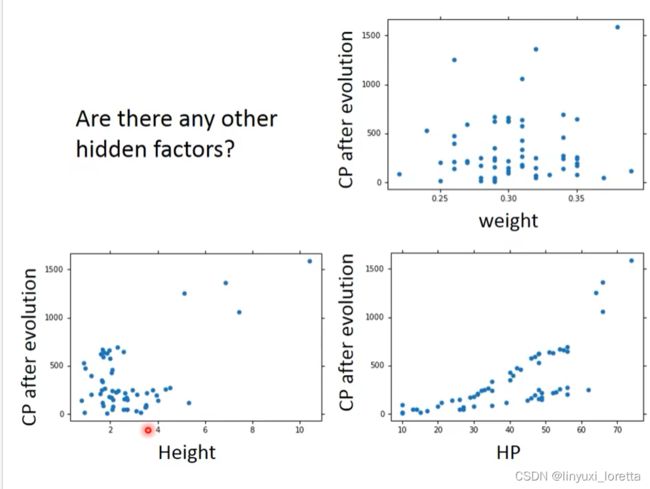
其实将Pokemons种类通过颜色区分，就会发现Pokemons种类是隐藏得比较深得特征，不同Pokemons种类影响了进化后的CP值的结果。

 

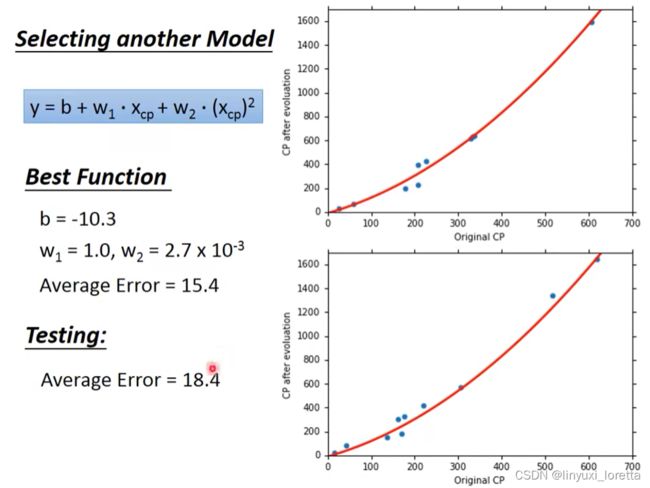
优化1，

通过对 Pokemons种类 判断，将 4个线性模型 合并到一个线性模型中

 

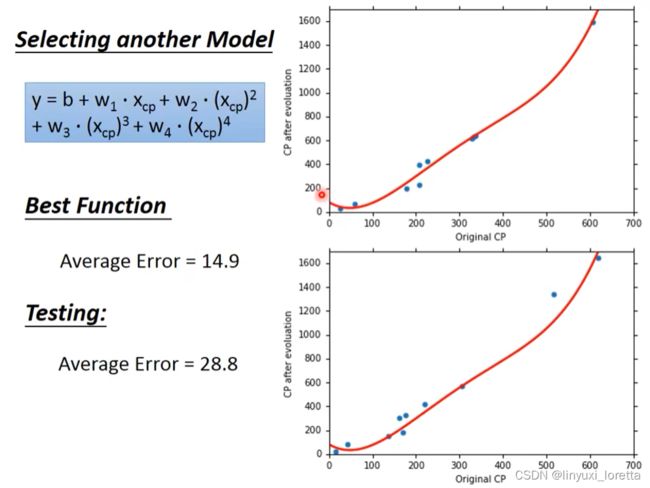
优化2：如果希望模型更强大表现更好（更多参数，更多input）

 

 如果有domain knowledge就知道要把什么样的东西加入model，怎么办？有一招把所有想到的东西统统加进去

解决方法：

 重新定义step2 一个func.是好是坏

w 越小，表示 function 较平滑的，即 输入变换时，输出比较不敏感

λ是hyper parameter

 

 

 b 的大小和function的平滑程度是没有关系的

总结

 

• Pokemon：原始的CP值和物种很大程度的决定了进化后的CP值，但可能还有其他的一些因素。
• Gradient descent：梯度下降的做法；后面会讲到它的理论依据和要点。
• Overfitting和Regularization：过拟合和正则化，主要介绍了表象；后面会讲到更多这方面的理论

今天用了testing set来选model，所以如果真的把系统放到线上，预期会得到更高的error rate，需要用validation的观念讲。

4-回归-演示_哔哩哔哩_bilibili

P4 回归-演示 (datawhalechina.github.io)

程式看上面的链接

lr = 1   随便设

诊断error的来源

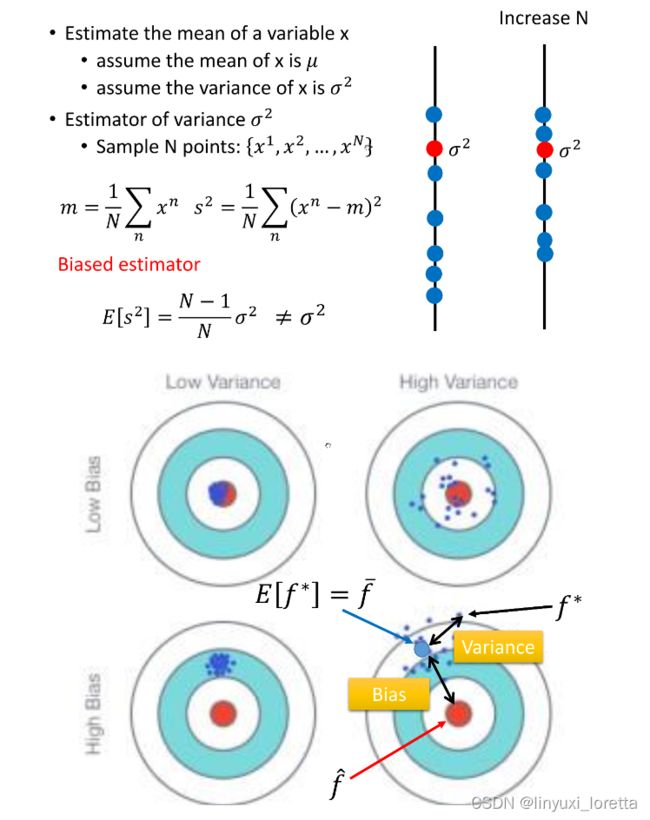
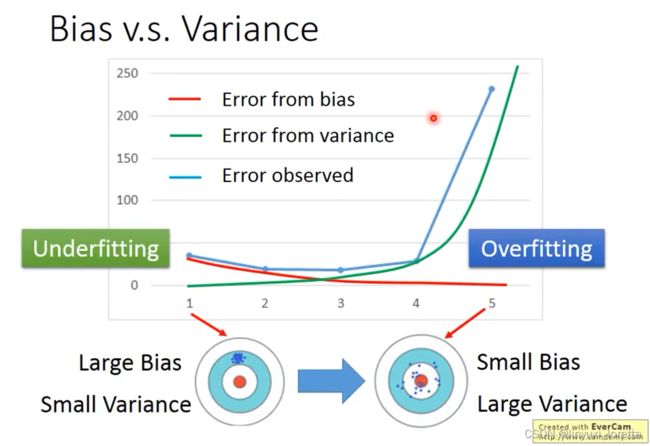
Error 的主要有两个来源，分别是 bias 和 variance 。

 

 

 做100次实验，每次都抓10只宝可梦。

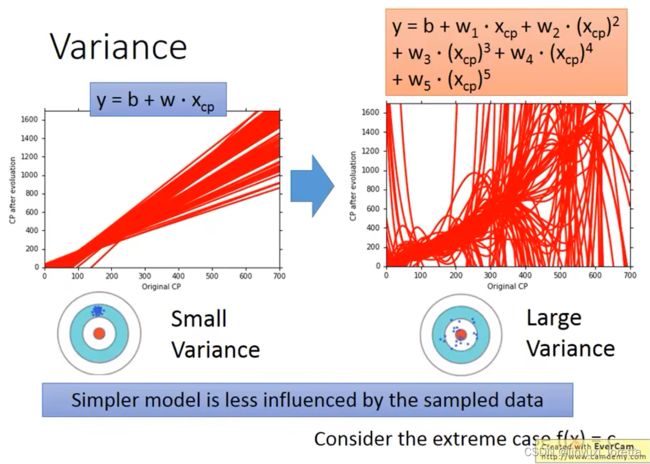
简单的model，small variance，因为   比较不会受不同data的影响

 

 如果error来自于Variance很大，overfitting

 如果error来自于bias很大，underfitting

知道error来自于哪，才知道后面要改进要走哪个方向

 

根据对问题的理解， 制造training data，e.g.手写数字辨识 ，将正常的数据集转15度；影像辨识，图片翻转；语音辨识，男生的声音用变声器转一下，公车上录一些杂讯、；language understanding，用翻译

 做regularization  可能伤害bias，需要调整 λ  

 

Adaptive learning rate

有一系列的方法，都是Ada- 开头，老师觉得现在Adam方法最稳定，式子略复杂

 举一个简单的思想：随着次数的增加，通过一些因子来减少学习率

e.g.  

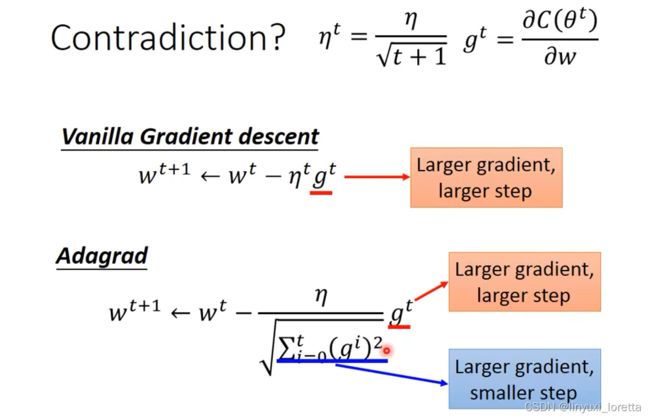
Adagrad

学习率不能是一个值通用所有特征，不同的参数需要不同的学习率

  

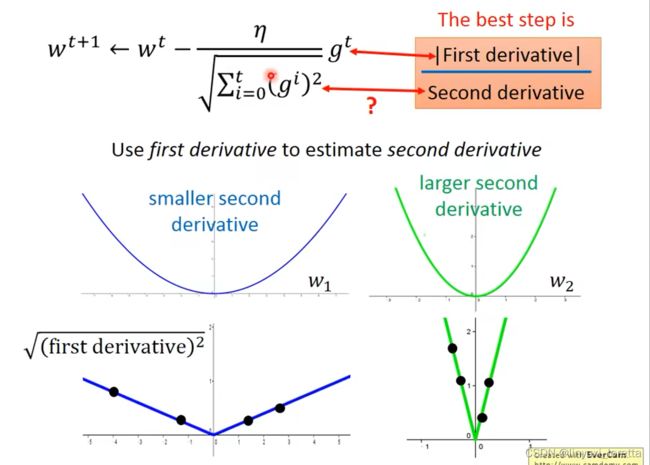
Adagrad 存在的矛盾？

Adagrad 强调反差效果

 

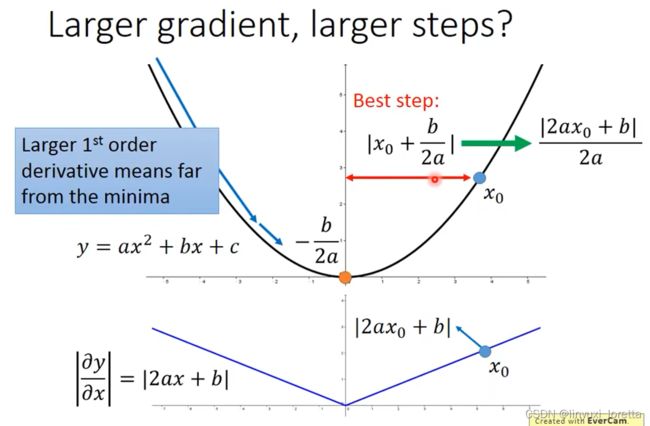
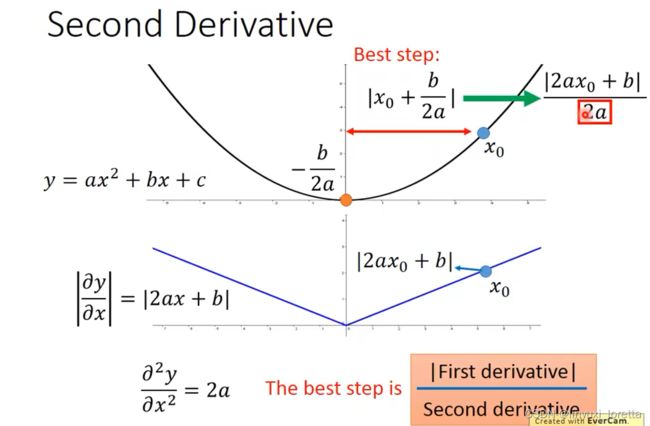
 结论1-1：微分越大，就跟最低点的距离越远。最好的步伐和微分的大小成正比。

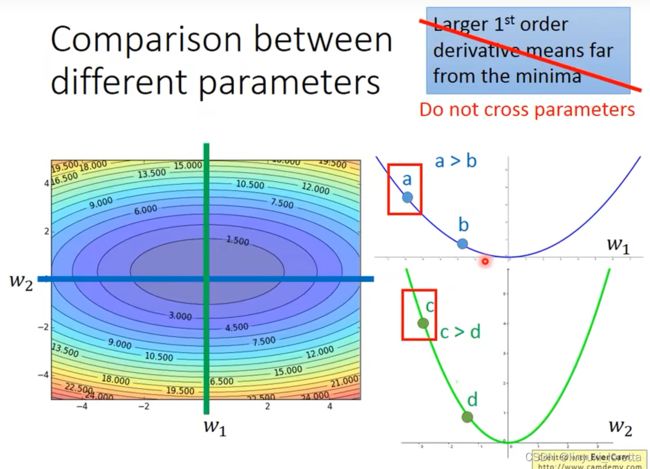
这个结论在多个参数的时候就不一定成立了。

多参数下结论不一定成立

 

 

 

Tip2：随机梯度下降法

随机梯度下降法stochastic gradient descent更快一点

 

常规梯度下降法走一步要处理到所有20个例子，但随机算法此时已经走了20步（每处理一个例子就更新）

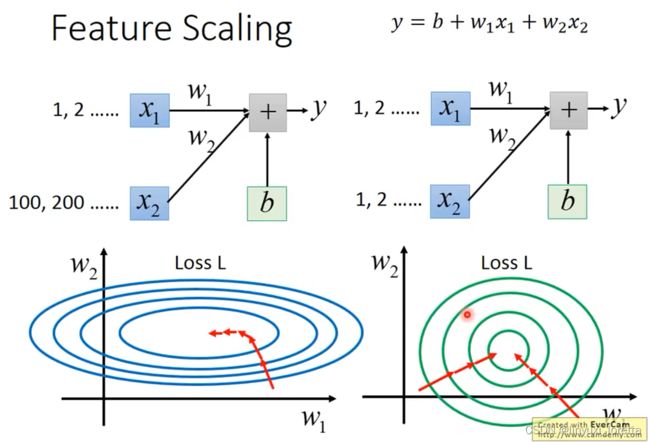
Tip3：特征缩放feature scaling

为什么要这样做？

对于左边的情况，上面讲过这种狭长的情形不过不用Adagrad的话是比较难处理的，两个方向上需要不同的学习率，同一组学习率会搞不定它。而右边情形更新参数就会变得比较容易。

左边的梯度下降并不是向着最低点方向走的，而是顺着等高线切线法线方向走的。但绿色就可以向着圆心（最低点）走，这样做参数更新也是比较有效率。

怎么做缩放？

方法非常多，这里举例一种常见的做法：

梯度下降的理论基础

接下来就是如果在小圆圈内快速的找到最小值？

泰勒展开式

 k代表微分的次数

 

 不考虑s的话，可以看出剩下的部分就是两个向量(△θ1​,△θ2​) 和 (u,v)的内积，那怎样让它最小，就是和向量 (u,v)方向相反的向量

这个式子有个前提，泰勒展开式给的approximation要够精确，红色的圈圈足够小（理论上learning rate要无穷小）

式1-2只考虑了泰勒展开式的一次项，如果考虑到二次项，理论上learning rate就可以设大一点（比如牛顿法），在实际中不是特别好，不划算。

梯度下降的限制

容易陷入local minima、saddle point，还有可能实际中只是当微分值小于某一个数值就停下来了，但这里只是比较平缓，并不是极值点

作业一

要知道一个问题能不能用machine learning的方法解，先看能不能formulate成 要找一个function