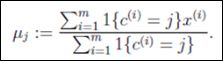python代码实现K-means聚类算法
第一部分:理论实战
- 概述
K-means算法是集简单和经典于一身的基于距离的聚类算法,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。
2,基本思想
通过迭代寻找k个类簇的一种划分方案,使得用这k个类簇的均值来代表相应各类样本时所得的总体误差最小。
k个聚类具有以下特点:各聚类本身尽可能的紧凑,而各聚类之间尽可能的分开。
k-means算法的基础是最小误差平方和准则
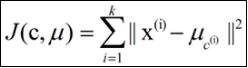
式中,μc(i)表示第i个聚类的均值
各类簇内的样本越相似,其与该类均值间的误差平方越小,对所有类所得到的误差平方求和,即可验证分为k类时,各聚类是否是最优的。
公式推导可参见:
https://blog.csdn.net/google19890102/article/details/51142299
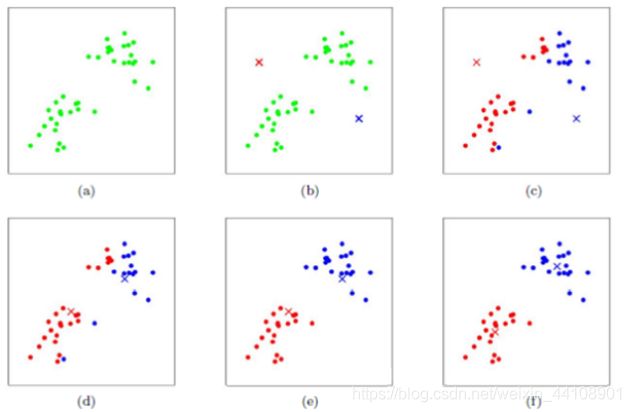
4、算法实现步骤:
k-means算法是将样本聚类成 k个簇(cluster),其中k是用户给定的,其求解过程非常直观简单,具体算法描述如下:
其伪代码如下:
创建k个点作为初始的质心点(随机选择)
当任意一个点的簇分配结果发生改变时
对数据集中的每一个数据点
对每一个质心
计算质心与数据点的距离
将数据点分配到距离最近的簇
对每一个簇,计算簇中所有点的均值,并将均值作为质心
5、python实战
#!/usr/bin/python
# coding=utf-8
from numpy import *
# 加载数据
def loadDataSet(fileName): # 解析文件,按tab分割字段,得到一个浮点数字类型的矩阵
dataMat = [] # 文件的最后一个字段是类别标签
fr = open(fileName)
for line in fr.readlines():
curLine = line.strip().split('\t')
fltLine = map(float, curLine) # 将每个元素转成float类型
dataMat.append(fltLine)
return dataMat
# 计算欧几里得距离
def distEclud(vecA, vecB):
return sqrt(sum(power(vecA - vecB, 2))) # 求两个向量之间的距离
# 构建聚簇中心,取k个(此例中为4)随机质心
def randCent(dataSet, k):
n = shape(dataSet)[1]
centroids = mat(zeros((k,n))) # 每个质心有n个坐标值,总共要k个质心
for j in range(n):
minJ = min(dataSet[:,j])
maxJ = max(dataSet[:,j])
rangeJ = float(maxJ - minJ)
centroids[:,j] = minJ + rangeJ * random.rand(k, 1)
return centroids
# k-means 聚类算法
def kMeans(dataSet, k, distMeans =distEclud, createCent = randCent):
m = shape(dataSet)[0]
clusterAssment = mat(zeros((m,2))) # 用于存放该样本属于哪类及质心距离
# clusterAssment第一列存放该数据所属的中心点,第二列是该数据到中心点的距离
centroids = createCent(dataSet, k)
clusterChanged = True # 用来判断聚类是否已经收敛
while clusterChanged:
clusterChanged = False;
for i in range(m): # 把每一个数据点划分到离它最近的中心点
minDist = inf; minIndex = -1;
for j in range(k):
distJI = distMeans(centroids[j,:], dataSet[i,:])
if distJI < minDist:
minDist = distJI; minIndex = j # 如果第i个数据点到第j个中心点更近,则将i归属为j
if clusterAssment[i,0] != minIndex: clusterChanged = True; # 如果分配发生变化,则需要继续迭代
clusterAssment[i,:] = minIndex,minDist**2 # 并将第i个数据点的分配情况存入字典
print centroids
for cent in range(k): # 重新计算中心点
ptsInClust = dataSet[nonzero(clusterAssment[:,0].A == cent)[0]] # 去第一列等于cent的所有列
centroids[cent,:] = mean(ptsInClust, axis = 0) # 算出这些数据的中心点
return centroids, clusterAssment
# --------------------测试----------------------------------------------------
# 用测试数据及测试kmeans算法
datMat = mat(loadDataSet('testSet.txt'))
myCentroids,clustAssing = kMeans(datMat,4)
print myCentroids
print clustAssing
6、K-means算法补充
K-means算法的缺点及改进方法
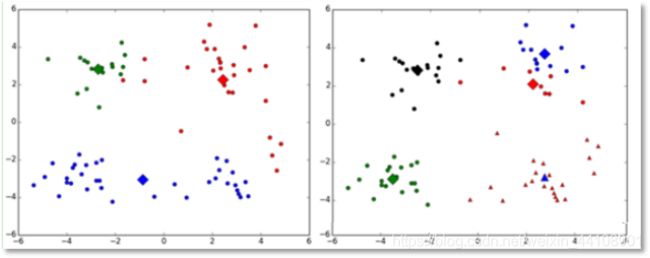
(1)k值的选择是用户指定的,不同的k得到的结果会有挺大的不同,如下图所示,左边是k=3的结果,这个就太稀疏了,蓝色的那个簇其实是可以再划分成两个簇的。而右图是k=5的结果,可以看到红色菱形和蓝色菱形这两个簇应该是可以合并成一个簇的:
改进:
对k的选择可以先用一些算法分析数据的分布,如重心和密度等,然后选择合适的k
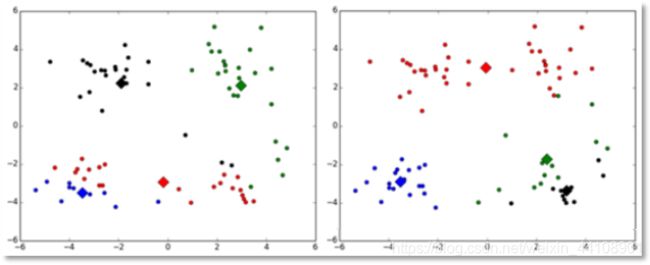
(2)对k个初始质心的选择比较敏感,容易陷入局部最小值。例如,我们上面的算法运行的时候,有可能会得到不同的结果,如下面这两种情况。K-means也是收敛了,只是收敛到了局部最小值:
改进:
有人提出了另一个成为二分k均值(bisecting k-means)算法,它对初始的k个质心的选择就不太敏感
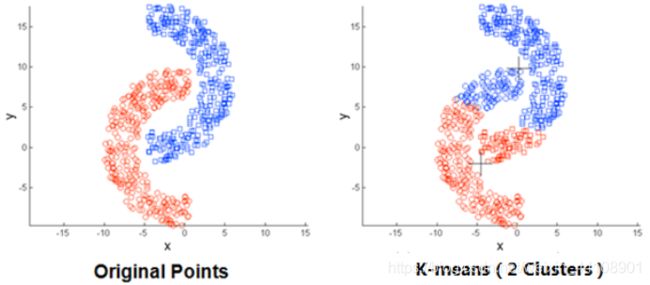
(3)存在局限性,如下面这种非球状的数据分布就搞不定了:
(4)数据集比较大的时候,收敛会比较慢。
第二部分:python3的简单实现
import numpy as np
import matplotlib.pyplot as plt
# 加载数据
def loadDataSet(fileName):
data = np.loadtxt(fileName,delimiter='\t')
return data
# 欧氏距离计算
def distEclud(x,y):
return np.sqrt(np.sum((x-y)**2)) # 计算欧氏距离
# 为给定数据集构建一个包含K个随机质心的集合
def randCent(dataSet,k):
m,n = dataSet.shape
centroids = np.zeros((k,n))
for i in range(k):
index = int(np.random.uniform(0,m)) #
centroids[i,:] = dataSet[index,:]
return centroids
# k均值聚类
def KMeans(dataSet,k):
m = np.shape(dataSet)[0] #行的数目
# 第一列存样本属于哪一簇
# 第二列存样本的到簇的中心点的误差
clusterAssment = np.mat(np.zeros((m,2)))
clusterChange = True
# 第1步 初始化centroids
centroids = randCent(dataSet,k)
while clusterChange:
clusterChange = False
# 遍历所有的样本(行数)
for i in range(m):
minDist = 100000.0
minIndex = -1
# 遍历所有的质心
#第2步 找出最近的质心
for j in range(k):
# 计算该样本到质心的欧式距离
distance = distEclud(centroids[j,:],dataSet[i,:])
if distance < minDist:
minDist = distance
minIndex = j
# 第 3 步:更新每一行样本所属的簇
if clusterAssment[i,0] != minIndex:
clusterChange = True
clusterAssment[i,:] = minIndex,minDist**2
#第 4 步:更新质心
for j in range(k):
pointsInCluster = dataSet[np.nonzero(clusterAssment[:,0].A == j)[0]] # 获取簇类所有的点
centroids[j,:] = np.mean(pointsInCluster,axis=0) # 对矩阵的行求均值
print("Congratulations,cluster complete!")
return centroids,clusterAssment
def showCluster(dataSet,k,centroids,clusterAssment):
m,n = dataSet.shape
if n != 2:
print("数据不是二维的")
return 1
mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', ', 'pr']
if k > len(mark):
print("k值太大了")
return 1
# 绘制所有的样本
for i in range(m):
markIndex = int(clusterAssment[i,0])
plt.plot(dataSet[i,0],dataSet[i,1],mark[markIndex])
mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', ', 'pb']
# 绘制质心
for i in range(k):
plt.plot(centroids[i,0],centroids[i,1],mark[i])
plt.show()
dataSet = loadDataSet("test.txt")
k = 4
centroids,clusterAssment = KMeans(dataSet,k)
showCluster(dataSet,k,centroids,clusterAssment)
第三部分:利用sklearn库实现
先实例推演一下:
1、数据准备
样列如下(每个样本有两个特征):
样本 X0 X1
1 7 5
2 5 7
3 7 7
4 3 3
5 4 6
6 1 4
7 0 0
8 2 2
9 8 7
10 6 8
11 5 5
12 3 7
用python演示一下
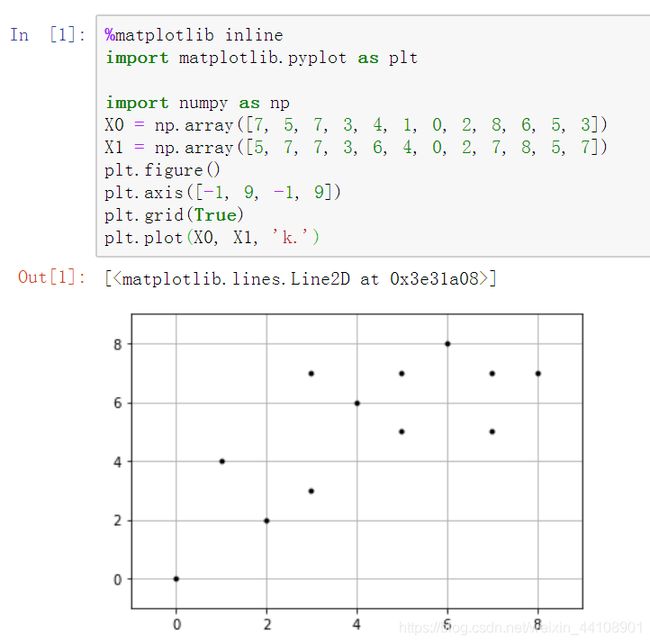
2、随机选取重心
假设K-Means初始化时,随机设定两个重心,将第一个类的重心设置在第5个样本,第二个类的重心设置在第11个样本.那么我们可以把每个实例与两个重心的距离都计算出来,将其分配到最近的类里面。计算结果如下表所示:
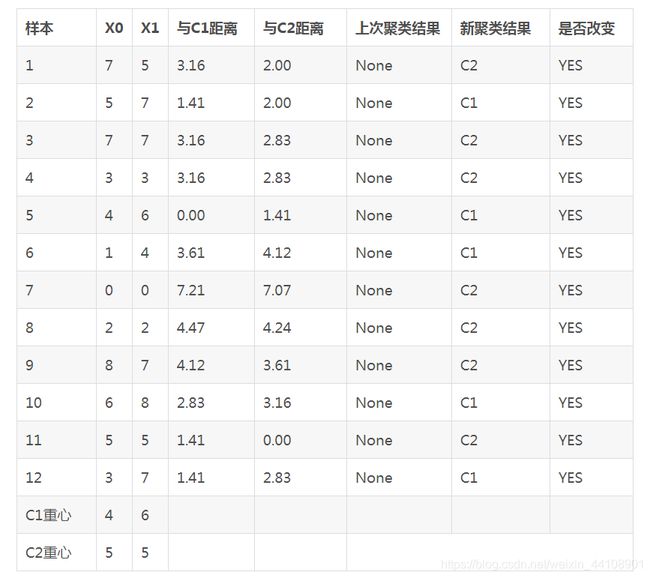
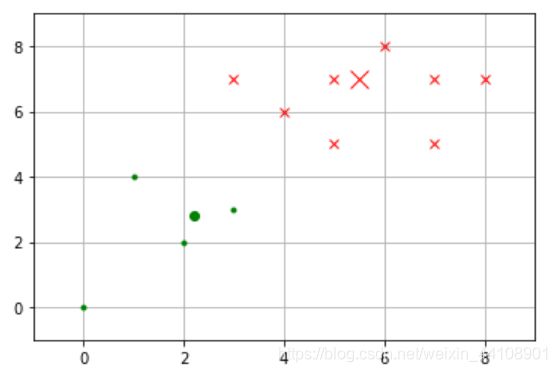
新的重心位置和初始聚类结果如下图所示。第一类用X表示,第二类用点表示。重心位置用稍大的点突出显示
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
X0 = np.array([7, 5, 7, 3, 4, 1, 0, 2, 8, 6, 5, 3])
X1 = np.array([5, 7, 7, 3, 6, 4, 0, 2, 7, 8, 5, 7])
# plt.figure()
# plt.axis([-1, 9, -1, 9])
# plt.grid(True)
# plt.plot(X0, X1, 'k.')
C1 = [1, 4, 5, 9, 11]#属于C1的index
C2 = list(set(range(12)) - set(C1))#属于C2的index
X0C1, X1C1 = X0[C1], X1[C1]#属于C1的坐标
X0C2, X1C2 = X0[C2], X1[C2]#属于C2的坐标
plt.figure()
plt.axis([-1, 9, -1, 9])
plt.grid(True)
plt.plot(X0C1, X1C1, 'rx')
plt.plot(X0C2, X1C2, 'g.')
plt.plot(4,6,'rx',ms=15.0)
plt.plot(5,5,'g.',ms=15.0)
效果图:
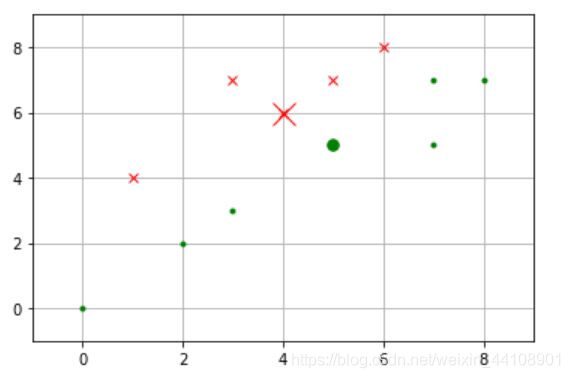
3、重算重心
接下来我们需要重新计算两个类的重心,把重心移动到新位置,并重新计算各个样本与新重心的距离,并根据距离远近为样本重新归类。结果如下表所示:
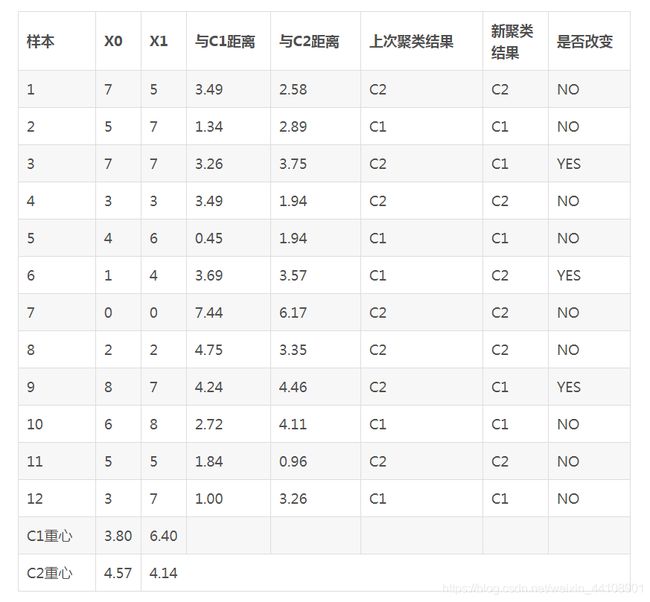
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
X0 = np.array([7, 5, 7, 3, 4, 1, 0, 2, 8, 6, 5, 3])
X1 = np.array([5, 7, 7, 3, 6, 4, 0, 2, 7, 8, 5, 7])
# plt.figure()
# plt.axis([-1, 9, -1, 9])
# plt.grid(True)
# plt.plot(X0, X1, 'k.')
C1 = [1, 2, 4, 8, 9, 11]
C2 = list(set(range(12)) - set(C1))
X0C1, X1C1 = X0[C1], X1[C1]
X0C2, X1C2 = X0[C2], X1[C2]
plt.figure()
plt.axis([-1, 9, -1, 9])
plt.grid(True)
plt.plot(X0C1, X1C1, 'rx')
plt.plot(X0C2, X1C2, 'g.')
plt.plot(3.8,6.4,'rx',ms=12.0)
plt.plot(4.57,4.14,'g.',ms=12.0)
效果图:
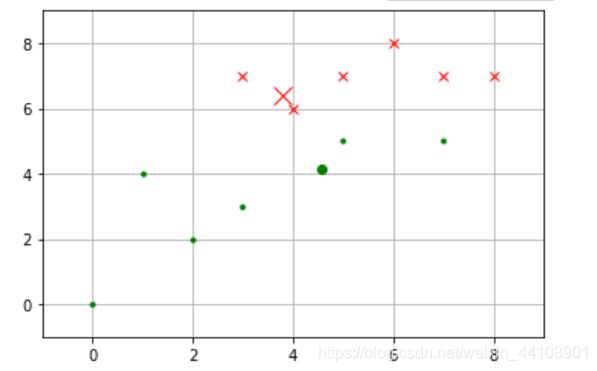
4、重复计算
接下来再重复一次上面的做法,把重心移动到新位置,并重新计算各个样本与新重心的距离,并根据距离远近为样本重新归类。结果如下表所示:

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
X0 = np.array([7, 5, 7, 3, 4, 1, 0, 2, 8, 6, 5, 3])
X1 = np.array([5, 7, 7, 3, 6, 4, 0, 2, 7, 8, 5, 7])
# plt.figure()
# plt.axis([-1, 9, -1, 9])
# plt.grid(True)
# plt.plot(X0, X1, 'k.')
C1 = [0, 1, 2, 4, 8, 9, 10, 11]
C2 = list(set(range(12)) - set(C1))
X0C1, X1C1 = X0[C1], X1[C1]
X0C2, X1C2 = X0[C2], X1[C2]
plt.figure()
plt.axis([-1, 9, -1, 9])
plt.grid(True)
plt.plot(X0C1, X1C1, 'rx')
plt.plot(X0C2, X1C2, 'g.')
plt.plot(5.5,7.0,'rx',ms=12.0)
plt.plot(2.2,2.8,'g.',ms=12.0)
sklearn中对于kmeans算法的参数:
参数:
n_clusters:整形,缺省值=8 【生成的聚类数,即产生的质心(centroids)数。】
max_iter:整形,缺省值=300
执行一次k-means算法所进行的最大迭代数。
n_init:整形,缺省值=10
用不同的质心初始化值运行算法的次数,最终解是在inertia意义下选出的最优结果。
init:有三个可选值:’k-means++’, ‘random’,或者传递一个ndarray向量。
此参数指定初始化方法,默认值为 ‘k-means++’。
(1)‘k-means++’ 用一种特殊的方法选定初始质心从而能加速迭代过程的收敛
(2)‘random’ 随机从训练数据中选取初始质心。
(3)如果传递的是一个ndarray,则应该形如 (n_clusters, n_features) 并给出初始质心。
precompute_distances:三个可选值,‘auto’,True 或者 False。
预计算距离,计算速度更快但占用更多内存。
(1)‘auto’:如果 样本数乘以聚类数大于 12million 的话则不预计算距离。This corresponds to about 100MB overhead per job using double precision.
(2)True:总是预先计算距离。
(3)False:永远不预先计算距离。
tol:float形,默认值= 1e-4 与inertia结合来确定收敛条件。
n_jobs:整形数。 指定计算所用的进程数。内部原理是同时进行n_init指定次数的计算。
(1)若值为 -1,则用所有的CPU进行运算。若值为1,则不进行并行运算,这样的话方便调试。
(2)若值小于-1,则用到的CPU数为(n_cpus + 1 + n_jobs)。因此如果 n_jobs值为-2,则用到的CPU数为总CPU数减1。
random_state:整形或 numpy.RandomState 类型,可选
用于初始化质心的生成器(generator)。如果值为一个整数,则确定一个seed。此参数默认值为numpy的随机数生成器。
copy_x:布尔型,默认值=True
当我们precomputing distances时,将数据中心化会得到更准确的结果。如果把此参数值设为True,则原始数据不会被改变。如果是False,则会直接在原始数据
上做修改并在函数返回值时将其还原。但是在计算过程中由于有对数据均值的加减运算,所以数据返回后,原始数据和计算前可能会有细小差别。
属性:
cluster_centers_:向量,[n_clusters, n_features] (聚类中心的坐标)
Labels_: 每个点的分类
inertia_:float形
每个点到其簇的质心的距离之和。
Notes:
这个k-means运用了 Lioyd’s 算法,平均计算复杂度是 O(knT),其中n是样本量,T是迭代次数。
计算复杂读在最坏的情况下为 O(n^(k+2/p)),其中n是样本量,p是特征个数。(D. Arthur and S. Vassilvitskii, ‘How slow is the k-means method?’ SoCG2006)
在实践中,k-means算法时非常快的,属于可实践的算法中最快的那一类。但是它的解只是由特定初始值所产生的局部解。所以为了让结果更准确真实,在实践中要用不同的初始值重复几次才可以。
Methods:
fit(X[,y]):
计算k-means聚类。
fit_predictt(X[,y]):
计算簇质心并给每个样本预测类别。
fit_transform(X[,y]):
计算簇并 transform X to cluster-distance space。
get_params([deep]):
取得估计器的参数。
predict(X):predict(X)
给每个样本估计最接近的簇。
score(X[,y]):
计算聚类误差
set_params(**params):
为这个估计器手动设定参数。
transform(X[,y]): 将X转换为群集距离空间。
在新空间中,每个维度都是到集群中心的距离。 请注意,即使X是稀疏的,转换返回的数组通常也是密集的。
sklearn实例实现:
import numpy as np
X0 = np.array([7, 5, 7, 3, 4, 1, 0, 2, 8, 6, 5, 3])
X1 = np.array([5, 7, 7, 3, 6, 4, 0, 2, 7, 8, 5, 7])
X = np.array(list(zip(X0, X1))).reshape(len(X0), 2)#压缩数据整合在一起
from sklearn.cluster import KMeans#导入KMeans包
km = KMeans(n_clusters=2).fit(X)#按照k=2进行计算
输出标簦:
km.labels_:
输出重心点:
centroids = km.cluster_centers_
print(centroids)
输出图形:
import matplotlib.pyplot as plt
plt.figure()
plt.scatter(X[:, 0], X[:, 1], c=km.labels_)#原始数据散点图,按照分类查看
centroids = km.cluster_centers_
plt.scatter(centroids[:, 0], centroids[:, 1],
marker='x', s=169, linewidths=3,
color='r', zorder=10)#重心红色X进行突出
输出权重比分:
from sklearn.cluster import KMeans
from sklearn import metrics
scores = []
for k in range(2,12):
labels = KMeans(n_clusters=k).fit(X).labels_
score = metrics.silhouette_score(X, labels)
scores.append(score)
scores
K-Means聚类算法实现鸢尾花数据的聚类:
#############K-means-鸢尾花聚类############
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
#from sklearn import datasets
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:] ##表示我们只取特征空间中的后两个维度
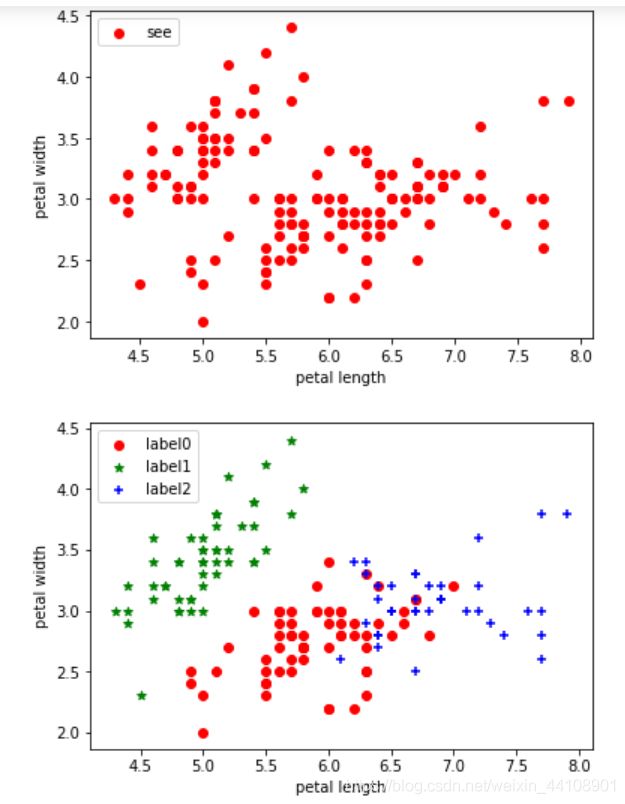
#绘制数据分布图
plt.scatter(X[:, 0], X[:, 1], c = "red", marker='o', label='see')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc=2)
plt.show()
estimator = KMeans(n_clusters=3)#构造聚类器
estimator.fit(X)#聚类
label_pred = estimator.labels_ #获取聚类标签
#绘制k-means结果
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
plt.scatter(x0[:, 0], x0[:, 1], c = "red", marker='o', label='label0')
plt.scatter(x1[:, 0], x1[:, 1], c = "green", marker='*', label='label1')
plt.scatter(x2[:, 0], x2[:, 1], c = "blue", marker='+', label='label2')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc=2)
plt.show()