机器学习练习2-逻辑回归
本文基于Andrew_Ng的ML课程作业
1-Logistic Regression with gradientDescent:根据申请学生两次测试的评分来决定他们是否被录取
导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt函数：Sigmoid函数
def sigmoid(z): #Sigmoid函数
return 1/(1+np.exp(-z))函数：计算代价函数J(theta)
def computeCost(X,y,theta): #计算代价函数J(theta)
first=np.multiply(-y,np.log(sigmoid(X*theta.T)+1e-5))
#epsilon = 1e-5 np.log(P + epsilon):计算log后的数值太大导致数据溢出,因此需要做一下数据精度的处理,这里修改浮点数精度为1e-5
second=np.multiply((1-y),np.log(1-sigmoid(X*theta.T)+1e-5))
return np.sum(first-second)/len(X)函数：梯度下降法
def gradientDescent(X,y,theta,alpha,iters): #梯度下降法
temp=np.matrix(np.zeros(theta.shape))
parameters=int(theta.ravel().shape[1])
cost=np.zeros(iters)
for i in range(iters):
error=(sigmoid(X*theta.T))-y
for j in range(parameters):
term=np.multiply(error,X[:,j])
temp[0,j]=theta[0,j]-(alpha/len(X))*np.sum(term)
theta=temp
cost[i]=computeCost(X,y,theta)
return cost,theta主函数：
# Logistic Regression with gradientDescent:根据申请学生两次测试的评分来决定他们是否被录取
path='ex2data1.txt'
data=pd.read_csv(path,header=None,names=['Exam 1','Exam 2','Admitted'])
positive=data[data['Admitted'].isin([1])]
#test_elements.isin([a]):判断数组element中的元素a是否属于test_elements;若为是返回True,若不是返回False
#最外面又套data:返回False的所有行被删除,返回True的所有行被保留
negative=data[data['Admitted'].isin([0])]
data.insert(0,'Ones',1)
cols=data.shape[1]
X=data.iloc[:,0:cols-1]
y=data.iloc[:,cols-1:cols]
X=np.matrix(X.values)
y=np.matrix(y.values)
theta=np.matrix(np.array([0,0,0]))
alpha=0.0000001
iters=10000
cost,g=gradientDescent(X,y,theta,alpha,iters)
x=np.linspace(30,100,num=100)
f=(-g[0,0]-g[0,1]*x)/g[0,2]
fig2,ax=plt.subplots(figsize=(9,6),dpi=128)
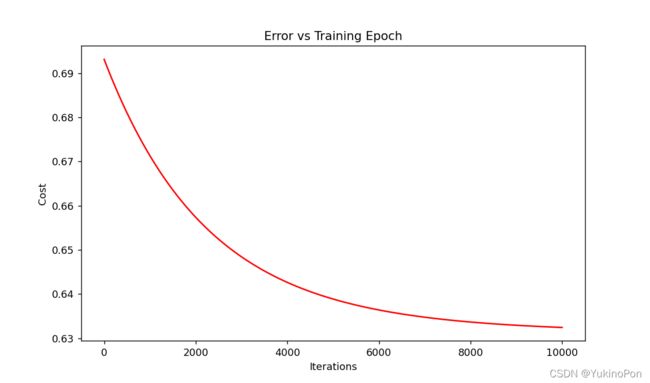
ax.plot(np.arange(iters),cost,'r') #np.arange(n):生成起点为0,终点为n-1的步长为1的排列
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs Training Epoch')
plt.show()
fig,ax=plt.subplots(figsize=(9,6),dpi=128)
ax.plot(x,f,'y',label='Prediction')
ax.scatter(positive['Exam 1'],positive['Exam 2'],s=50,c='b',marker='o',label="Admitted")
ax.scatter(negative['Exam 1'],negative['Exam 2'],s=50,c='r',marker='x',label='Not Admitted')
ax.legend(loc='upper right')
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()代价函数-迭代次数
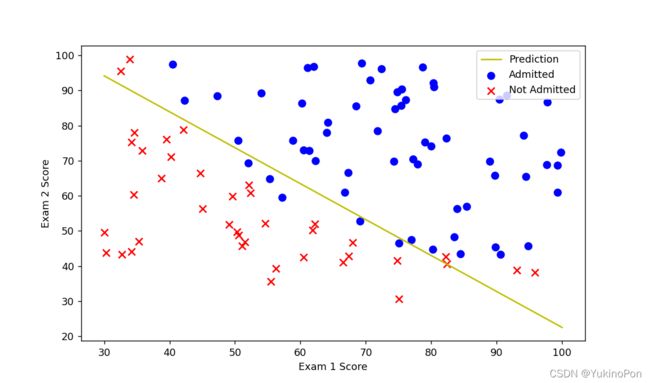
预测结果
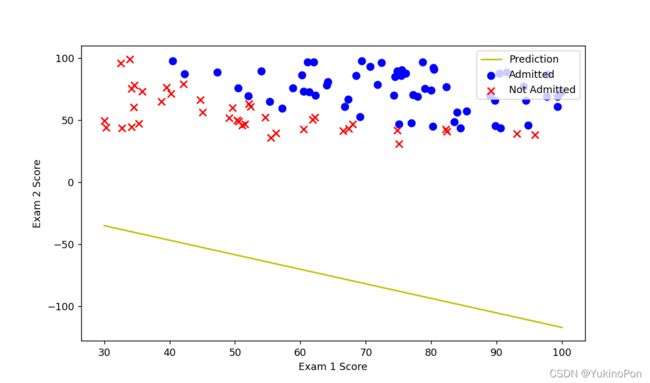可以看到，自己写代码实现梯度下降、自己定义迭代次数和步长，很难确定合适的学习率alpha从而分隔Admitted和Not Admitted，所以在下一种方法中，我们不自己写代码实现梯度下降，我们调用一个已有的库scipy.optimize.fmin_tnc，我们不用自己定义迭代次数和步长，功能会直接告诉我们最优解。
2-Logistic Regression with scipy.optimize.fmin_tnc:根据申请学生两次测试的评分来决定他们是否被录取
导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt函数：Sigmoid函数
def sigmoid(z): #Sigmoid函数
return 1/(1+np.exp(-z))函数：计算代价函数J(theta)
def computeCost(theta,X,y): #计算代价函数J(theta)
theta=np.matrix(theta)
X=np.matrix(X)
y=np.matrix(y)
first=np.multiply(-y,np.log(sigmoid(X*theta.T)))
second=np.multiply((1-y),np.log(1-sigmoid(X*theta.T)))
return np.sum(first-second)/len(X)函数：计算梯度grad(梯度函数)
def computeGradient(theta,X,y): #计算梯度grad
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
parameters=int(theta.ravel().shape[1])
grad = np.zeros(parameters) #np.zeros()括号内是parameters是为了让grad是数组,若括号内为theta.shape,grad是矩阵
error=(sigmoid(X*theta.T))-y
for i in range(parameters):
term=np.multiply(error,X[:,i])
grad[i]=np.sum(term)/len(X)
return grad函数：预测函数
def predict(theta,X): #预测函数
probability=sigmoid([email protected])
return [1 if x>= 0.5 else 0 for x in probability]主函数：
# Logistic Regression with scipy.optimize.fmin_tnc:根据申请学生两次测试的评分来决定他们是否被录取
path='ex2data1.txt'
data=pd.read_csv(path,header=None,names=['Exam 1','Exam 2','Admitted'])
positive=data[data['Admitted'].isin([1])]
#test_elements.isin([a]):判断数组element中的元素a是否属于test_elements;若为是返回True,若不是返回False
#最外面又套data:返回False的所有行被删除,返回True的所有行被保留
negative=data[data['Admitted'].isin([0])]
data.insert(0,'Ones',1)
cols=data.shape[1]
X=data.iloc[:,0:cols-1]
y=data.iloc[:,cols-1:cols]
X=np.array(X.values)
y=np.array(y.values)
theta_init=np.zeros(3)
#用scipy.optimize.fmin_tnc求解参数
result=opt.fmin_tnc(func=computeCost,x0=theta_init,fprime=computeGradient,args=(X,y))
#scipy.optimize.fmin_tnc(func,x0,fprime=None,args=(),approx_grad=0):约束最小化多元标量函数:解决有约束(提供梯度信息)的多元函数问题
#参数:func:优化的目标函数;x0:初值;fprime:提供优化函数func的梯度函数,不然优化函数func必须返回函数值和梯度,或设置approx_grad=True;approx_grad:如果设置为True,会给出近似梯度;args:元组,是传递给优化函数的参数
#返回:x数组,返回的优化问题目标值;nfeval:整数,function evaluations的数目(在进行优化的时候,每当目标优化函数被调用一次,就算一个function evaluation。在一次迭代过程中会有多次function evaluation。这个参数不等同于迭代次数,而往往大于迭代次数);rc:整数,Return code,成功为1,不成功为0并给出失败信息
#由于args(传递给优化函数的参数)是元组/列表,所以X,y在函数内才转化为矩阵,在函数外是列表
x=np.linspace(30,100,num=100)
f=(-result[0][0]-result[0][1]*x)/result[0][2] #线性决策边界为:theta_0+theta_1*x+theta_2*y=0
fig,ax=plt.subplots(figsize=(9,6),dpi=128)
ax.plot(x,f,'y',label='Prediction')
ax.scatter(positive['Exam 1'],positive['Exam 2'],s=50,c='b',marker='o',label="Admitted")
ax.scatter(negative['Exam 1'],negative['Exam 2'],s=50,c='r',marker='x',label='Not Admitted')
ax.legend(loc='upper right')
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()
theta=np.matrix(result[0])
predictions=predict(theta,X)
correct=[1 if ((a==1 and b==1) or (a==0 and b==0)) else 0 for (a,b) in zip(predictions,y)] #zip(a,b):将列表a,b相应位置的元素打包为元组存放在列表中
accuracy=sum(list(map(int,correct)))/len(correct) #map(function,iterable):对某个序列以给定的函数格式作映射,function为函数/数据类型
print('accuracy={:.2%}'.format(accuracy)) #format():数字格式化:百分比格式:{:.2%}(保留两位小数)预测准确率
预测结果
3-Regularized Logistic Regression with scipy.optimize.fmin_tnc:根据芯片在两次测试中的测试结果决定芯片被接受或抛弃
导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt函数：Sigmoid函数
def sigmoid(z): #Sigmoid函数
return 1/(1+np.exp(-z))函数：计算正则化的代价函数J(theta)
def computeRegCost(theta,X,y,lambada): #计算正则化的代价函数J(theta)
theta=np.matrix(theta)
X=np.matrix(X)
y=np.matrix(y)
first=np.multiply(-y,np.log(sigmoid(X*theta.T)))
second=np.multiply((1-y),np.log(1-sigmoid(X*theta.T)))
reg=(lambada/(2*len(X)))*np.sum(np.power(theta[:,1:theta.shape[1]],2)) #matrix[:,1:matrix.shape[1]]:取矩阵的第一列直到最后一列(左闭右闭)
return np.sum(first-second)/len(X)+reg函数：计算正则化的梯度grad
def computeRegGradient(theta,X,y,lambada): #计算正则化的梯度grad
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
parameters=int(theta.ravel().shape[1])
grad = np.zeros(parameters)
error=(sigmoid(X*theta.T))-y
for i in range(parameters):
term=np.multiply(error,X[:,i])
if (i==0): #theta_0的梯度单独更新
grad[i]=np.sum(term)/len(X)
else:
grad[i]=np.sum(term)/len(X)+(lambada/len(X))*theta[:,i]
return grad函数：预测函数
def predict(theta,X): #预测函数
probability=sigmoid([email protected])
return [1 if x>= 0.5 else 0 for x in probability]函数：多项式假设函数
def hfunc(theta,x1,x2): #多项式假设函数
temp=theta[0][0] #temp就是多项式假设函数y=theta_0*x1^m*x2^n+...
place=0
for i in range(1,degree+1):
for j in range(0,i+1):
temp+=np.power(x1,i-j)*np.power(x2,j)*theta[0][place+1]
place+=1
return temp函数：找到决策曲线
def find_decision_boundary(theta): #找到决策曲线
t1=np.linspace(-1,1.5,1000) #正则化后的数据都在(-1,1.5)之间
t2=np.linspace(-1,1.5,1000)
cordinates=[(x1,x2) for x1 in t1 for x2 in t2]
x1_cord,x2_cord=zip(*cordinates)
#zip(*coordinates):把列表coordinates中 原来列表中对应元素被压缩为元组放入列表中 解压为 原来列表变成元组放入一个新列表
h_val=pd.DataFrame({'x1':x1_cord,'x2':x2_cord})
# pd.DataFrame({'col1':list/tuple,'col2':list/tuple}):使用字典创建DataFrame:默认生成整数索引,字典的键作列,值作行
h_val['hval']=hfunc(theta,h_val['x1'],h_val['x2'])
decision=h_val[np.abs(h_val['hval'])<2*10**-3] #找到所有预测结果几乎为0(边界条件)的行 #对这个式子写法的理解:排除h_val中h_val['h_val']绝对值小于10**-6的,保留剩下的行
return decision['x1'],decision['x2'] #或decision.x1,decision.x2主函数：
# Regularized Logistic Regression with scipy.optimize.fmin_tnc:根据芯片在两次测试中的测试结果决定芯片被接受或抛弃
path='ex2data2.txt'
data=pd.read_csv(path,header=None,names=['Test 1','Test 2','Accepted'])
positive=data[data['Accepted'].isin([1])]
negative=data[data['Accepted'].isin([0])]
#Feature Mapping:特征映射,创造多项式类型的更多特征
#也正是因为使用特征映射创造多项式特征后容易导致过拟合,所以通过正则化解决过拟合的问题
degree=6 #由于现在数据集不能直接用直线分割,需要用曲线分割,所以为每组数据创造更多的特征:这里为x_1,x_2添加最高到6次幂的特征
x1=data['Test 1']
x2=data['Test 2']
data.insert(3,'Ones',1) #在data最后添加全为1的新列
data.drop(['Test 1'],axis=1,inplace=True)
data.drop(['Test 2'],axis=1,inplace=True)
#删去data前两列数据,接下里要为每组数据创造更多的特征
#DataFrame.drop([],axis=0,inplace=True):删除行/列|参数:axis=0删除行=1删除列;inplace=False保持原数据不变,True在原数据上改变
#np.power(x,i):x的i次方
for i in range(1,degree+1): #列名:F_x1指数_x2指数;指数范围:-1<=i-j<=i,i+1>=j>=0(x1和x2的指数之和=i遍历从1-->6)
for j in range(0,i+1):
data['F'+str(i-j)+str(j)]=np.power(x1,i-j)*np.power(x2,j)
cols=data.shape[1]
X=data.iloc[:,1:cols]
y=data.iloc[:,0:1]
theta=np.zeros(cols-1)
X=np.array(X.values)
y=np.array(y.values)
lambada=100
#用scipy.optimize.fmin_tnc求解参数
result=opt.fmin_tnc(func=computeRegCost,x0=theta,fprime=computeRegGradient,args=(X,y,lambada))
theta=np.matrix(result[0])
predictions=predict(theta,X)
correct=[1 if ((a==1 and b==1) or (a==0 and b==0)) else 0 for (a,b) in zip(predictions,y)] #zip(a,b):将列表a,b相应位置的元素打包为元组存放在列表中
accuracy=sum(list(map(int,correct)))/len(correct) #map(function,iterable):对某个序列以给定的函数格式作映射,function为函数/数据类型
print('accuracy={:.2%}'.format(accuracy)) #format():数字格式化:百分比格式:{:.2%}(保留两位小数)
fig,ax=plt.subplots(figsize=(12,8),dpi=128)
ax.scatter(positive['Test 1'], positive['Test 2'], s=50, c='b', marker='o', label='Accepted')
ax.scatter(negative['Test 1'], negative['Test 2'], s=50, c='r', marker='x', label='Rejected')
ax.set_xlabel('Test 1 Score')
ax.set_ylabel('Test 2 Score')
x1,x2=find_decision_boundary(result)
plt.scatter(x1,x2,c='y',s=10,label='Prediction')
ax.legend(loc='upper right')
plt.show()预测准确率
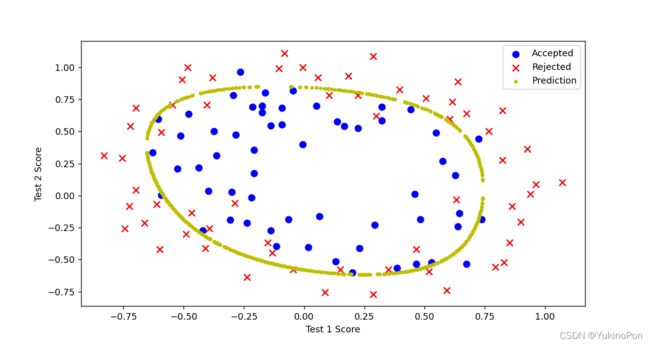
预测结果
修改λ，λ=0时过拟合
预测准确率
预测结果
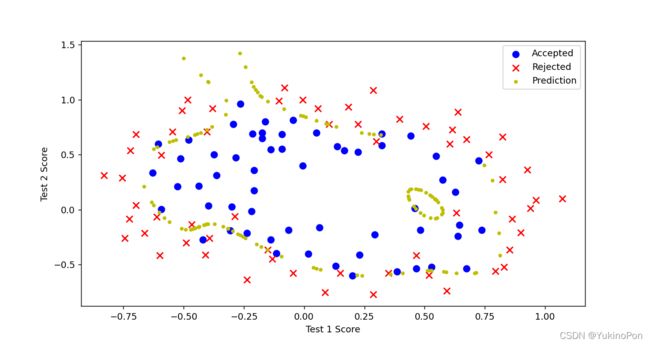
修改λ，λ=100时欠拟合
预测准确率
预测结果
4-Regularized Logistic Regression in scikit-learn:根据芯片在两次测试中的测试结果决定芯片被接受或抛弃
导入库
import numpy as np
import pandas as pd
from sklearn import linear_model #调用sklearn的线性回归包主函数：
# Regularized Logistic Regression in scikit-learn:根据芯片在两次测试中的测试结果决定芯片被接受或抛弃
path='ex2data2.txt'
data=pd.read_csv(path,header=None,names=['Test 1','Test 2','Accepted'])
positive=data[data['Accepted'].isin([1])]
negative=data[data['Accepted'].isin([0])]
degree=6
x1=data['Test 1']
x2=data['Test 2']
data.insert(3,'Ones',1)
data.drop(['Test 1'],axis=1,inplace=True)
data.drop(['Test 2'],axis=1,inplace=True)
for i in range(1,degree+1):
for j in range(0,i+1):
data['F'+str(i-j)+str(j)]=np.power(x1,i-j)*np.power(x2,j)
cols=data.shape[1]
X=data.iloc[:,1:cols]
y=data.iloc[:,0:1]
X=np.array(X.values)
y=np.array(y.values)
#以上为同3-的数据处理方法
model=linear_model.LogisticRegression(penalty='l2',C=1.0) #C:正则化系数λ的倒数,float类型,默认为1.0,越小的数值表示越强的正则化
model.fit(X,y.ravel())
print('accuracy={:.2%}'.format(model.score(X,y))) #model.score(X,y):预测准确率
h=model.predict(X) #model.predict(X):预测结果
print(h)预测准确率
预测结果
