动手深度学习：计算机视觉——语义分割

目录

图像分割和实例分割

Pascal VOC2012 语义分割数据集

预处理数据

自定义语义分割数据集类

读取数据集

整合所有组件

转置卷积

填充、步幅和多通道

与矩阵变换的联系

使用矩阵乘法来实现卷积

使用矩阵乘法来实现转置卷积

使用全卷积网络FCN进行语义分割

构造模型

特征提取层

1×1卷积层和转置卷积层

初始化转置卷积层

读取数据集

训练

​编辑

预测

需要注意的函数

net.children()和list

F.cross_entropy

切片

---

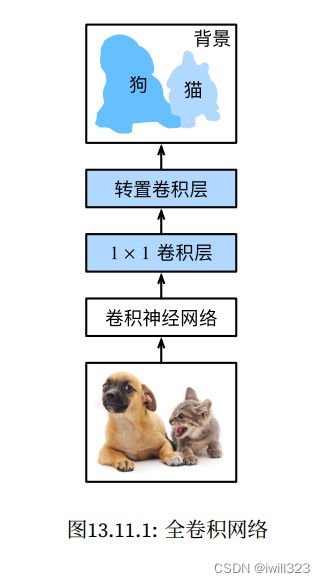
目标检测问题中，我们一直使用方形边界框来标注和预测图像中的目标。 而语义分割（semantic segmentation）可以识别并理解图像中每一个像素的内容，其语义区域的标注和预测是像素级的。 下图展示了语义分割中图像有关狗、猫和背景的标签。 与目标检测相比，语义分割标注的像素级的边框显然更加精细。

图像分割和实例分割

计算机视觉领域还有2个与语义分割相似的重要问题，即图像分割（image segmentation）和实例分割（instance segmentation）。

• 图像分割将图像划分为若干组成区域，这类问题的方法通常利用图像中像素之间的相关性。它在训练时不需要有关图像像素的标签信息，在预测时也无法保证分割出的区域具有我们希望得到的语义。以 上图图像作为输入，图像分割可能会将狗分为两个区域：一个覆盖以黑色为主的嘴和眼睛，另一个覆盖以黄色为主的其余部分身体。
• 实例分割也叫同时检测并分割（simultaneous detection and segmentation），它研究如何识别图像中各个目标实例的像素级区域。与语义分割不同，实例分割不仅需要区分语义，还要区分不同的目标实例。例如，如果图像中有两条狗，则实例分割需要区分像素属于的两条狗中的哪一条。

Pascal VOC2012 语义分割数据集

最重要的语义分割数据集之一是Pascal VOC2012，数据集的tar文件大约为2GB，位于../data/VOCdevkit/VOC2012

%matplotlib inline
import os
import torch
from torch import nn
from torch.nn import functional as F
import torchvision
from PIL import Image
from d2l import torch as d2l

d2l.DATA_HUB['voc2012'] = (d2l.DATA_URL + 'VOCtrainval_11-May-2012.tar',
'4e443f8a2eca6b1dac8a6c57641b67dd40621a49')
voc_dir = d2l.download_extract('voc2012', 'VOCdevkit/VOC2012')

进入路径../data/VOCdevkit/VOC2012之后，我们可以看到数据集的不同组件。 ImageSets/Segmentation路径包含用于训练和测试样本的文本文件，而JPEGImages和SegmentationClass路径分别存储着每个示例的输入图像和标签。 此处的标签也采用图像格式，其尺寸和它所标注的输入图像的尺寸相同。 此外，标签中颜色相同的像素属于同一个语义类别。 下面将read_voc_images函数定义为将所有输入的图像和标签读入内存。

def read_voc_images(voc_dir, is_train=True):
    """读取所有VOC图像并标注"""
    txt_fname = os.path.join(voc_dir, 'ImageSets', 'Segmentation',
                             'train.txt' if is_train else 'val.txt')
    mode = torchvision.io.image.ImageReadMode.RGB
    with open(txt_fname, 'r') as f:
        images = f.read().split()
    features, labels = [], []
    for i, fname in enumerate(images):
        features.append(torchvision.io.read_image(os.path.join(
            voc_dir, 'JPEGImages', f'{fname}.jpg')))
        labels.append(torchvision.io.read_image(os.path.join(
            voc_dir, 'SegmentationClass' ,f'{fname}.png'), mode))
    return features, labels

train_features, train_labels = read_voc_images(voc_dir, True)

如果报错，参考No such operator image::read_file问题解决_iwill323的博客-CSDN博客

下面绘制前5个输入图像及其标签。 在标签图像中，白色和黑色分别表示边框和背景，而其他颜色则对应不同的类别。

标签图像的颜色是固定的，RGB颜色值和类名：

VOC_COLORMAP = [[0, 0, 0], [128, 0, 0], [0, 128, 0], [128, 128, 0],
                [0, 0, 128], [128, 0, 128], [0, 128, 128], [128, 128, 128],
                [64, 0, 0], [192, 0, 0], [64, 128, 0], [192, 128, 0],
                [64, 0, 128], [192, 0, 128], [64, 128, 128], [192, 128, 128],
                [0, 64, 0], [128, 64, 0], [0, 192, 0], [128, 192, 0],
                [0, 64, 128]]


VOC_CLASSES = ['background', 'aeroplane', 'bicycle', 'bird', 'boat',
               'bottle', 'bus', 'car', 'cat', 'chair', 'cow',
               'diningtable', 'dog', 'horse', 'motorbike', 'person',
               'potted plant', 'sheep', 'sofa', 'train', 'tv/monitor']

通过上面定义的两个常量，我们可以方便地查找标签中每个像素的类索引。 我们定义了voc_colormap2label函数来构建从上述RGB颜色值到类别索引的映射，而voc_label_indices函数将RGB值映射到在Pascal VOC2012数据集中的类别索引。注意，对RGB颜色值采用了256进制的操作，以便于迅速索引。

#@save
def voc_colormap2label():
    """构建从RGB到VOC类别索引的映射"""
    colormap2label = torch.zeros(256 ** 3, dtype=torch.long)
    for i, colormap in enumerate(VOC_COLORMAP):
        colormap2label[
            (colormap[0] * 256 + colormap[1]) * 256 + colormap[2]] = i
        # 将RGB三通道像素值按照R*256*256+G*256+B的方法算成一个像素值，
        # 再把这个值作为字典索引，相当于采用256进制，所以这个索引是唯一的
    return colormap2label

#@save
def voc_label_indices(colormap, colormap2label):
    """将VOC标签中的RGB值映射到它们的类别索引"""
    colormap = colormap.permute(1, 2, 0).numpy().astype('int32') # 将通道放在最后一维
    idx = ((colormap[:, :, 0] * 256 + colormap[:, :, 1]) * 256
           + colormap[:, :, 2])  # numpy()类型，正常的乘号和加号运算
    return colormap2label[idx]

例如，在第一张样本图像中，飞机头部区域的类别索引为1，而背景索引为0

y = voc_label_indices(train_labels[0], voc_colormap2label()) # train_labels指标签图片
y[105:115, 130:140], VOC_CLASSES[1]

(tensor([[0, 0, 0, 0, 0, 0, 0, 0, 0, 1],
         [0, 0, 0, 0, 0, 0, 0, 1, 1, 1],
         [0, 0, 0, 0, 0, 0, 1, 1, 1, 1],
         [0, 0, 0, 0, 0, 1, 1, 1, 1, 1],
         [0, 0, 0, 0, 0, 1, 1, 1, 1, 1],
         [0, 0, 0, 0, 1, 1, 1, 1, 1, 1],
         [0, 0, 0, 0, 0, 1, 1, 1, 1, 1],
         [0, 0, 0, 0, 0, 1, 1, 1, 1, 1],
         [0, 0, 0, 0, 0, 0, 1, 1, 1, 1],
         [0, 0, 0, 0, 0, 0, 0, 0, 1, 1]]),
 'aeroplane')

预处理数据

图片分类中我们可以把图片resize到统一大小。如果语义分割也采用resize处理数据，那么预测的像素类别也要重新映射回原始尺寸的输入图像。resize拉伸的时候中间的像素是通过插值法得到的，而标签是包含一个个像素的标签的，这样的映射可能不够精确，尤其在不同语义的分割区域，所以语义分割的图像不用resize。

在语义分割中，为了使图片大小一样，我们一般是将图像裁剪为和标签相同大小的区域（使用transforms.RandomCrop，裁剪输入图像和标签（图片）的相同区域）。

输入图像随机裁剪，有随机成分，标签是固定的，如何与标签对应？下面函数中get_params允许裁剪之后的区域返回边框的坐标数值（边界框），*rect就是把边界框四个坐标展开，这样对图片和标号做同样的裁剪

def voc_rand_crop(feature, label, height, width):
    """随机裁剪特征和标签图像"""
    rect = torchvision.transforms.RandomCrop.get_params(
        feature, (height, width))
    feature = torchvision.transforms.functional.crop(feature, *rect)
    label = torchvision.transforms.functional.crop(label, *rect)
    return feature, label


imgs = []
for _ in range(n):
    imgs += voc_rand_crop(train_features[0], train_labels[0], 200, 300)

imgs = [img.permute(1, 2, 0) for img in imgs]
d2l.show_images(imgs[::2] + imgs[1::2], 2, n);

自定义语义分割数据集类

通过继承高级API提供的Dataset类，自定义了一个语义分割数据集类VOCSegDataset。 通过实现__getitem__函数，我们可以任意访问数据集中索引为idx的输入图像及其每个像素的类别索引。 由于数据集中有些图像的尺寸可能小于随机裁剪所指定的输出尺寸，这些样本可以通过自定义的filter函数移除掉。 此外，我们还定义了normalize_image函数，从而对输入图像的RGB三个通道的值分别做标准化。

#@save
class VOCSegDataset(torch.utils.data.Dataset):
    """一个用于加载VOC数据集的自定义数据集"""

    def __init__(self, is_train, crop_size, voc_dir):
        self.transform = torchvision.transforms.Normalize(
            mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
        self.crop_size = crop_size
        features, labels = read_voc_images(voc_dir, is_train=is_train)
        self.features = [self.normalize_image(feature)
                         for feature in self.filter(features)]
        self.labels = self.filter(labels)
        self.colormap2label = voc_colormap2label()
        print('read ' + str(len(self.features)) + ' examples')

    def normalize_image(self, img):
        return self.transform(img.float() / 255)

    def filter(self, imgs):
        return [img for img in imgs if (
            img.shape[1] >= self.crop_size[0] and
            img.shape[2] >= self.crop_size[1])]

    def __getitem__(self, idx):
        feature, label = voc_rand_crop(self.features[idx], self.labels[idx],
                                       *self.crop_size)
        return (feature, voc_label_indices(label, self.colormap2label))

    def __len__(self):
        return len(self.features)

读取数据集

指定随机裁剪的输出图像的形状为320×480， 下面我们可以查看训练集和测试集所保留的样本个数

crop_size = (320, 480)
voc_train = VOCSegDataset(True, crop_size, voc_dir)
voc_test = VOCSegDataset(False, crop_size, voc_dir)

read 1114 examples
read 1078 examples

设批量大小为64，定义训练集的迭代器。 打印第一个小批量的形状会发现：与图像分类或目标检测不同，这里的标签是一个三维数组。

batch_size = 64
train_iter = torch.utils.data.DataLoader(voc_train, batch_size, shuffle=True,
                                    drop_last=True,
                                    num_workers=d2l.get_dataloader_workers())
for X, Y in train_iter:
    print(X.shape)
    print(Y.shape)
    break

torch.Size([64, 3, 320, 480])
torch.Size([64, 320, 480])

整合所有组件

定义以下load_data_voc函数来下载并读取Pascal VOC2012语义分割数据集。 它返回训练集和测试集的数据迭代器

def load_data_voc(batch_size, crop_size):
    """加载VOC语义分割数据集"""
    voc_dir = d2l.download_extract('voc2012', os.path.join(
        'VOCdevkit', 'VOC2012'))
    num_workers = d2l.get_dataloader_workers()
    train_iter = torch.utils.data.DataLoader(
        VOCSegDataset(True, crop_size, voc_dir), batch_size,
        shuffle=True, drop_last=True, num_workers=num_workers)
    test_iter = torch.utils.data.DataLoader(
        VOCSegDataset(False, crop_size, voc_dir), batch_size,
        drop_last=True, num_workers=num_workers)
    return train_iter, test_iter

转置卷积

一般的卷积神经网络，将图片送入卷积层之后，逐步缩小图片的尺寸，增大感受野，提取不同尺度的特征。然而语义分割需要输入和输出图像的空间维度相同，因为其输入图片和标号图片的像素标签是一一对应的。为了解决这一点，在空间维度被卷积神经网络层缩小后，可以使用转置卷积（transposed convolution），上采样增加中间层feature map的空间维度。

还有一个重要的区别：转置卷积是不含偏置的
一般操作是图片经过一系列卷积层缩小尺寸之后，加一个1×1卷积层减小channel，再用转置卷积层恢复图片大小。

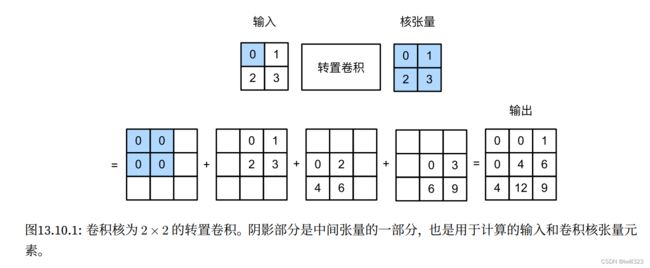
暂时忽略通道，设步幅为1且没有填充。 假设我们有一个ℎ×的输入张量和一个ℎ×的卷积核。 以步幅为1滑动卷积核窗口，每行次，每列ℎ次，共产生ℎ个中间结果，每个中间结果都是一个(ℎ+ℎ−1)×(+−1)的张量（包括0元素）。 为了计算每个中间张量，输入张量中的每个元素都要乘以卷积核，从而使所得的ℎ×张量替换中间张量的一部分。 请注意，每个中间张量被替换部分的位置与输入张量中元素的位置相对应。 最后，所有中间结果相加以获得最终结果。

例如，下图解释了如何为2×2的输入张量计算卷积核为2×2的转置卷积。

 

 可以对输入矩阵X和卷积核矩阵K实现基本的转置卷积运算trans_conv

def trans_conv(X, K):
    h, w = K.shape
    Y = torch.zeros((X.shape[0] + h - 1, X.shape[1] + w - 1))
    for i in range(X.shape[0]):
        for j in range(X.shape[1]):
            Y[i: i + h, j: j + w] += X[i, j] * K
    return Y

与常规卷积相比，转置卷积通过卷积核“广播”输入元素，从而产生大于输入的输出。

X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
trans_conv(X, K)

tensor([[ 0.,  0.,  1.],
        [ 0.,  4.,  6.],
        [ 4., 12.,  9.]])

当输入X和卷积核K都是四维张量时，可以使用高级API获得相同的结果。

X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2)
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, bias=False)
tconv.weight.data = K
tconv(X)

tensor([[[[ 0.,  0.,  1.],
          [ 0.,  4.,  6.],
          [ 4., 12.,  9.]]]], grad_fn=)

填充、步幅和多通道

与常规卷积不同，在转置卷积中，填充被应用于输出。 例如，当将高和宽两侧的填充数指定为1时，转置卷积的输出中将删除第一和最后的行与列

tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, padding=1, bias=False)
tconv.weight.data = K
tconv(X)

tensor([[[[4.]]]], grad_fn=)

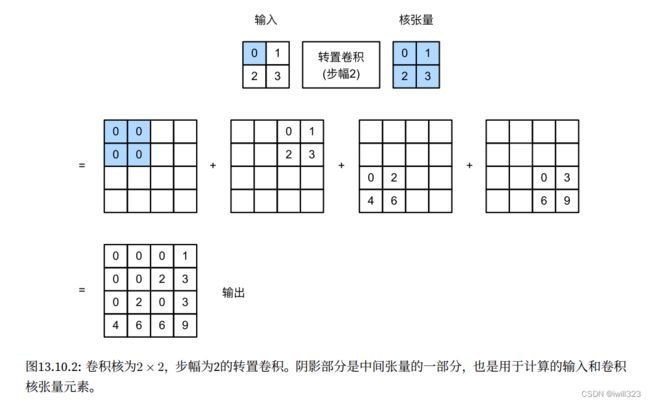
在转置卷积中，步幅被指定为中间结果（输出），而不是输入。 使用相同输入和卷积核张量，将步幅从1更改为2会增加中间张量的高和权重：

tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, stride=2, bias=False)
tconv.weight.data = K
tconv(X)

tensor([[[[0., 0., 0., 1.],
          [0., 0., 2., 3.],
          [0., 2., 0., 3.],
          [4., 6., 6., 9.]]]], grad_fn=)

对于多个输入和输出通道，转置卷积与常规卷积以相同方式运作。 假设输入有个通道，且转置卷积为每个输入通道分配了一个ℎ×的卷积核张量。当指定多个输出通道时，每个输出通道将有一个×ℎ×的卷积核。

同样，如果我们将代入卷积层来输出=()，并创建一个与具有相同的超参数、但输出通道数量是中通道数的转置卷积层，那么()的形状将与相同。

X = torch.rand(size=(1, 10, 16, 16))
conv = nn.Conv2d(10, 20, kernel_size=5, padding=2, stride=3)
tconv = nn.ConvTranspose2d(20, 10, kernel_size=5, padding=2, stride=3)
tconv(conv(X)).shape == X.shape

True

与矩阵变换的联系

转置卷积为何以矩阵变换命名呢？

使用矩阵乘法来实现卷积

卷积层是一种特殊的全连接层。对于全连接层，每个输入和每个输出都有连接，因此参数数量巨大。卷积层的核心思想是权重共享，每个输出只和部分输入连接，因此权重是稀疏矩阵。计算机后台在做卷积的时候，会将每个通道的卷积核变成一个行向量，将输入区域的感受野“拉成”向量，让后将卷积核矩阵和输入矩阵相乘，实际上还是做矩阵乘法，这样计算也更高效。

定义了一个3×3的输入X和2×2卷积核K，计算卷积输出Y。注意bias要设置为0

X = torch.arange(9.0).reshape(1, 1, 3, 3)
K = torch.tensor([[1.0, 2.0], [3.0, 4.0]]).reshape(1, 1, 2, 2)
conv = nn.Conv2d(1, 1, 2)
conv.weight.data, conv.bias.data = K, torch.tensor([0])
Y = conv(X)
Y

tensor([[27., 37.],
        [57., 67.]])

接下来，我们将卷积核K重写为包含大量0的稀疏权重矩阵W，形状是（4，9），其中非0元素来自卷积核K

def kernel2matrix(K):
    k, W = torch.zeros(5), torch.zeros((4, 9))
    k[:2], k[3:5] = K[0, :], K[1, :]
    W[0, :5], W[1, 1:6], W[2, 3:8], W[3, 4:] = k, k, k, k
    return W

W = kernel2matrix(K)
W

tensor([[1., 2., 0., 3., 4., 0., 0., 0., 0.],
        [0., 1., 2., 0., 3., 4., 0., 0., 0.],
        [0., 0., 0., 1., 2., 0., 3., 4., 0.],
        [0., 0., 0., 0., 1., 2., 0., 3., 4.]])

逐行连结输入X，获得了一个长度为9的矢量。 然后，W的矩阵乘法和向量化的X给出了一个长度为4的向量。 reshape之后，可以获得与上面的原始卷积操作所得相同的结果Y：使用矩阵乘法实现了卷积。

torch.matmul(W, X.reshape(-1)).reshape(2, 2)

tensor([[27., 37.],
        [57., 67.]])

使用矩阵乘法来实现转置卷积

同样，可以使用矩阵乘法来实现转置卷积。 将上面的常规卷积2×2的输出Y作为转置卷积的输入（实际上Y可以是任何2×2的值）。想要通过矩阵相乘来实现它，只需要将权重矩阵W转置

# Y = torch.rand([2,2])  # 任意输入
Z = trans_conv(Y, K)
Z == torch.matmul(W.T, Y.reshape(-1)).reshape(3, 3)

抽象来看，给定输入向量和权重矩阵，卷积的前向传播函数可以通过=来实现。 由于反向传播遵循链式法则和∇=⊤，卷积的反向传播函数可以通过将输入与转置的权重矩阵⊤相乘来实现。 因此，转置卷积层是对卷积层的正向传播函数和反向传播函数的交换：它的正向传播和反向传播函数将输入向量分别与⊤和相乘。

大概的意思是：从矩阵乘法的角度，转置卷积使用权重矩阵（这种权重矩阵不是常说的权重矩阵，而是由卷积核变换得到稀疏矩阵）的转置与输入相乘，所以是“转置”卷积

使用全卷积网络FCN进行语义分割

全卷积网络（fully convolutional network，FCN）采用卷积神经网络实现了从图像像素到像素类别的变换。FCN通过转置卷积，将中间层特征图的高和宽变换回输入图像的尺寸，输出的类别预测与输入图像在像素级别上具有一一对应关系：通道维的输出即该位置对应像素的类别预测。

构造模型

全卷积网络先使用CNN抽取图像特征，然后通过1×1卷积层将通道数变换为类别个数，最后通过转置卷积层将feature map的高和宽变换为输入图像的尺寸。

特征提取层

使用在ImageNet数据集上预训练的ResNet-18模型来提取图像特征，并将该网络记为pretrained_net。 ResNet-18模型的最后几层包括全局平均池化层和全连接层，然而全卷积网络中不需要它们。

pretrained_net = torchvision.models.resnet18(pretrained=True)
list(pretrained_net.children())[-3:]

[Sequential(
   (0): BasicBlock(
     (conv1): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
     ……
     (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      ……
     )
   )
   (1): BasicBlock(
      ……
   )
 ),
 AdaptiveAvgPool2d(output_size=(1, 1)),
 Linear(in_features=512, out_features=1000, bias=True)]

创建一个全卷积网络net。 它复制了ResNet-18中大部分的预训练层，除了最后的全局平均池化层和最接近输出的全连接层。

net = nn.Sequential(*list(pretrained_net.children())[:-2])

给定高度为320和宽度为480的输入，net的前向传播将输入的高和宽减小至原来的1/32，即10和15。

X = torch.rand(size=(1, 3, 320, 480))
net(X).shape

torch.Size([1, 512, 10, 15])

1×1卷积层和转置卷积层

使用1×1卷积层将输出通道数转换为Pascal VOC2012数据集的类数（21类）。

将feature map的高度和宽度增加32倍，从而将其变回输入图像的高和宽。卷积层输出形状的计算方法： 由于(320−64+16×2)/32+1=10且(480−64+16×2)/32+1=15，构造一个步幅为32的转置卷积层，并将卷积核的高和宽设为64，填充为16。 我们可以看到如果步幅为，填充为/2（假设/2是整数）且卷积核的高和宽为2，转置卷积核会将输入的高和宽分别放大倍。

注意转置卷积的输出通道就是num_classes，将每个像素点上num_classes个输入视作提取的特征，根据这些特征再提取出num_classes个分类值

num_classes = 21
net.add_module('final_conv', nn.Conv2d(512, num_classes, kernel_size=1))
net.add_module('transpose_conv', nn.ConvTranspose2d(num_classes, num_classes,
                                    kernel_size=64, padding=16, stride=32))

初始化转置卷积层

在图像处理中，我们有时需要将图像放大，即上采样（upsampling）。 双线性插值（bilinear interpolation） 是常用的上采样方法之一，它也经常用于初始化转置卷积层。

为了解释双线性插值，假设给定输入图像，我们想要计算上采样输出图像上的每个像素。

1. 将输出图像的坐标(,)映射到输入图像的坐标(′,′)上。 例如，根据输入与输出的size之比来映射。 请注意，映射后的′和′是实数（不一定是整数）。
2. 在输入图像上找到离坐标(′,′)最近的4个像素。
3. 输出图像在坐标(,)上的像素依据输入图像上这4个像素及它们与(′,′)的相对距离来计算。

双线性插值的上采样可以通过转置卷积层实现，内核由以下bilinear_kernel函数构造。 限于篇幅，我们只给出bilinear_kernel函数的实现，不讨论算法的原理。

def bilinear_kernel(in_channels, out_channels, kernel_size):
    factor = (kernel_size + 1) // 2
    if kernel_size % 2 == 1:
        center = factor - 1
    else:
        center = factor - 0.5
    og = (torch.arange(kernel_size).reshape(-1, 1),
          torch.arange(kernel_size).reshape(1, -1))
    filt = (1 - torch.abs(og[0] - center) / factor) * \
           (1 - torch.abs(og[1] - center) / factor)
    weight = torch.zeros((in_channels, out_channels,
                          kernel_size, kernel_size))
    weight[range(in_channels), range(out_channels), :, :] = filt
    return weight

双线性插值的上采样实验。 构造一个将输入的高和宽放大2倍的转置卷积层，并将其卷积核用bilinear_kernel函数初始化。

conv_trans = nn.ConvTranspose2d(3, 3, kernel_size=4, padding=1, stride=2,
                                bias=False)
conv_trans.weight.data.copy_(bilinear_kernel(3, 3, 4));

读取图像X，将上采样的结果记作Y。为了打印图像，需要调整通道维的位置

img = torchvision.transforms.ToTensor()(Image.open('../img/catdog.jpg'))
X = img.unsqueeze(0)
Y = conv_trans(X)
out_img = Y[0].permute(1, 2, 0).detach()

可以看到，转置卷积层将图像的高和宽分别放大了2倍。 除了坐标刻度不同，双线性插值放大的图像和原图看上去没什么两样。

d2l.set_figsize()
print('input image shape:', img.permute(1, 2, 0).shape)
d2l.plt.imshow(img.permute(1, 2, 0));
print('output image shape:', out_img.shape)
d2l.plt.imshow(out_img);

input image shape: torch.Size([561, 728, 3])
output image shape: torch.Size([1122, 1456, 3])

在全卷积网络中，我们用双线性插值的上采样初始化转置卷积层。对于1×1卷积层，我们使用Xavier初始化参数。

W = bilinear_kernel(num_classes, num_classes, 64)
net.transpose_conv.weight.data.copy_(W);

读取数据集

 指定随机裁剪的输出图像的形状为320×480：高和宽都可以被32整除（net的前向传播将输入的高和宽减小至原来的1/3）。

batch_size, crop_size = 32, (320, 480)
train_iter, test_iter = load_data_voc(batch_size, crop_size)

read 1114 examples
read 1078 examples

训练

损失函数和准确率计算与图像分类中的没有本质上的不同，我们使用转置卷积层的通道来预测像素的类别，F.cross_entropy会自动在通道维上进行损失计算。

假设模型输入是torch.rand(size=(64, 3, 320, 480))，经过net()前向传播，预测结果的形状是[64, 21, 320, 480]。那么对于loss()函数，inputs的形状是[64, 21, 320, 480]，同时targets的形状是torch.Size([64, 320, 480])，输出的结果形状是torch.Size([64, 320, 480])，即在每个像素点上有一个损失。loss函数使用两个mean(1)来计算得到每个样本的损失均值

此外，模型基于每个像素的预测类别是否正确来计算准确率。

def loss(inputs, targets):
    return F.cross_entropy(inputs, targets, reduction='none').mean(1).mean(1)


def train(net, train_iter, test_iter, loss, trainer, num_epochs,
               devices=d2l.try_all_gpus()):
    """Train a model with mutiple GPUs """
    timer, num_batches = d2l.Timer(), len(train_iter)
    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0, 1],
                            legend=['train loss', 'train acc', 'test acc'])
    net = nn.DataParallel(net, device_ids=devices).to(devices[0])
    for epoch in range(num_epochs):
        # Sum of training loss, sum of training accuracy, no. of examples,
        # no. of predictions
        metric = d2l.Accumulator(4)
        for i, (features, labels) in enumerate(train_iter):
            timer.start()
            l, acc = train_batch(
                net, features, labels, loss, trainer, devices)
            metric.add(l, acc, labels.shape[0], labels.numel())
            timer.stop()
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                             (metric[0] / metric[2], metric[1] / metric[3],
                              None))
        test_acc = evaluate_accuracy_gpu(net, test_iter)
        animator.add(epoch + 1, (None, None, test_acc))
    print(f'loss {metric[0] / metric[2]:.3f}, train acc '
          f'{metric[1] / metric[3]:.3f}, test acc {test_acc:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec on '
          f'{str(devices)}')

def train_batch(net, X, y, loss, trainer, devices):
    """Train for a minibatch with mutiple GPUs (defined in Chapter 13).

    Defined in :numref:`sec_image_augmentation`"""
    if isinstance(X, list):
        # Required for BERT fine-tuning (to be covered later)
        X = [x.to(devices[0]) for x in X]
    else:
        X = X.to(devices[0])
    y = y.to(devices[0])
    net.train()
    trainer.zero_grad()
    pred = net(X)
    l = loss(pred, y)
    l.sum().backward()
    trainer.step()
    train_loss_sum = l.sum()
    train_acc_sum = d2l.accuracy(pred, y)
    return train_loss_sum, train_acc_sum


def evaluate_accuracy_gpu(net, data_iter, device=None):
    """Compute the accuracy for a model on a dataset using a GPU.

    Defined in :numref:`sec_lenet`"""
    if isinstance(net, nn.Module):
        net.eval()  # Set the model to evaluation mode
        if not device:
            device = next(iter(net.parameters())).device
    # No. of correct predictions, no. of predictions
    metric = d2l.Accumulator(2)

    with torch.no_grad():
        for X, y in data_iter:
            if isinstance(X, list):
                # Required for BERT Fine-tuning (to be covered later)
                X = [x.to(device) for x in X]
            else:
                X = X.to(device)
            y = y.to(device)
            metric.add(d2l.accuracy(net(X), y), d2l.size(y))
    return metric[0] / metric[1]

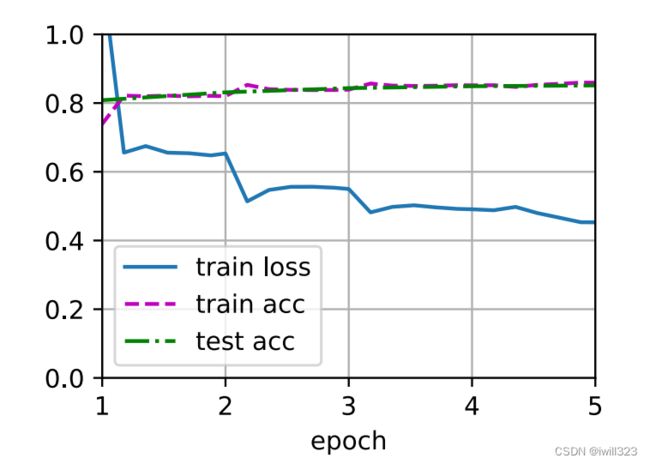
num_epochs, lr, wd, devices = 5, 0.001, 1e-3, d2l.try_all_gpus()
trainer = torch.optim.SGD(net.parameters(), lr=lr, weight_decay=wd)
train(net, train_iter, test_iter, loss, trainer, num_epochs, devices)

loss 0.453, train acc 0.859, test acc 0.851
259.0 examples/sec on [device(type='cuda', index=0), device(type='cuda', index=1)]

预测

在预测时，需要将输入图像在各个通道做标准化，并转成卷积神经网络所需要的四维输入格式。predict只接受一张图片，normalize_image(img)函数是自定义的。

假设模型输入是torch.rand(size=(64, 3, 320, 480))，经过net()前向传播，预测结果的形状是[64, 21, 320, 480]，argmax(dim=1)使得pred的形状是假设模型输入是torch.rand(size=(64, 3, 320, 480))，经过net()前向传播，预测结果的形状是[64, 320, 480]，即对每一个像素点得到一个预测的类别。由于img只是一张图片，所以reshape操作相当于把第0维去掉

def predict(img):
    X = test_iter.dataset.normalize_image(img).unsqueeze(0)
    pred = net(X.to(devices[0])).argmax(dim=1)
    return pred.reshape(pred.shape[1], pred.shape[2])

为了可视化预测的类别给每个像素，将预测类别映射回它们在数据集中的标注颜色。需要注意的是，和一般的切片不同，X是一个矩阵，所以切分出来的结果是一个三维的向量[X.shape[1],  X.shape[2], 3]

def label2image(pred):
    colormap = torch.tensor(d2l.VOC_COLORMAP, device=devices[0])
    X = pred.long()
    return colormap[X, :]

测试数据集中的图像大小和形状各异。 由于模型使用了步幅为32的转置卷积层，因此当输入图像的高或宽无法被32整除时，转置卷积层输出的高或宽会与输入图像的尺寸有偏差。 为了解决这个问题，我们可以在图像中截取多块高和宽为32的整数倍的矩形区域，并分别对这些区域中的像素做前向传播。 请注意，这些区域的并集需要完整覆盖输入图像。当一个像素被多个区域所覆盖时，它在不同区域前向传播中转置卷积层输出的平均值可以作为softmax运算的输入，从而预测类别。

为简单起见，我们只读取几张较大的测试图像，并从图像的左上角开始截取形状为320×480的区域用于预测。 对于这些测试图像，我们逐一打印它们截取的区域，再打印预测结果，最后打印标注的类别。

voc_dir = d2l.download_extract('voc2012', 'VOCdevkit/VOC2012')
test_images, test_labels = d2l.read_voc_images(voc_dir, False)
n, imgs = 4, []
for i in range(n):
    crop_rect = (0, 0, 320, 480)
    X = torchvision.transforms.functional.crop(test_images[i], *crop_rect)
    pred = label2image(predict(X))
    imgs += [X.permute(1,2,0), pred.cpu(),
             torchvision.transforms.functional.crop(
                 test_labels[i], *crop_rect).permute(1,2,0)]
d2l.show_images(imgs[::3] + imgs[1::3] + imgs[2::3], 3, n, scale=2);

需要注意的函数

net.children()和list

从模型中取出每一个模块

>>net = torchvision.models.resnet18(pretrained=True)

>>net

ResNet(
  (conv1): Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
  (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (relu): ReLU(inplace=True)
  (maxpool): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
  (layer1): Sequential(
      ……
  )
  (layer2): Sequential(
    (0): BasicBlock(
      (conv1): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (downsample): Sequential(
        (0): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)
        (1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (1): BasicBlock(
      ……
    )
  )
  (layer3): Sequential(
   ……
  )
  (layer4): Sequential(
    ……
  )
  (avgpool): AdaptiveAvgPool2d(output_size=(1, 1))
  (fc): Linear(in_features=512, out_features=1000, bias=True)
)

>>type(net)

>>type(net.children())

配合list使用

>>list(net.children())[0]

Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)

>>list(net.children())[1]

BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)

>>list(net.children())[5]

Sequential(
  (0): BasicBlock(
    (conv1): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
    (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (relu): ReLU(inplace=True)
    (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
    (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (downsample): Sequential(
      (0): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)
      (1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (1): BasicBlock(
    ……
  )
)

>>list(net.children())[5][0]

BasicBlock(
  (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
  (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (relu): ReLU(inplace=True)
  (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
  (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)

>>list(net.children())[5][0].downsample

Sequential(
  (0): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)
  (1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)

>>list(net.children())[5][0].downsample[0]

Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)

F.cross_entropy

input (Tensor) : Predicted unnormalized scores (often referred to as logits);

• Shape: (C),  (N, C) or (N, C, d_1, d_2, ..., d_K) with K  in the case of K-dimensional loss.

target (Tensor) : Ground truth class indices or class probabilities;

• If containing class indices, shape (), (N) or (N, d_1, d_2, ..., d_K) with K in the case of K-dimensional loss where each value should be between [0, C).
• If containing class probabilities, same shape as the input and each value should be between [0, 1].

>>inputs = torch.randn([64, 3, 320, 480], dtype = torch.float)
>>targets = torch.randint(3, (64, 320, 480), dtype = torch.int64)
>>F.cross_entropy(inputs, targets)

tensor(1.3904)

>>F.cross_entropy(inputs, targets, reduction='none').shape

torch.Size([64, 320, 480])

切片

一般对矩阵使用的切片，在某一维中截取一个列表，切片后矩阵的shape和原矩阵的shape相同，比如一个二维数组，切片后的结果还是二维矩阵。

在某一维的切片也可以是一个矩阵，按照该矩阵的元素在该维上“采样”，比如下面的color[idx, 1]，在列上取第一列，在行上按照idx的元素取行数

>>color = torch.randint(8, [4, 5])
>>color

tensor([[2, 1, 0, 1, 7],
        [0, 5, 1, 6, 7],
        [6, 0, 6, 4, 0],
        [3, 6, 6, 1, 6]])

>>idx = torch.randint(4, [2, 3])

tensor([[2, 2, 1],
        [2, 1, 0]])

>>color[idx, 1]

tensor([[0, 0, 5],
        [0, 5, 1]])

>>color[idx, idx]

tensor([[6, 6, 5],
        [6, 5, 2]])

>>color[idx, :]

tensor([[[6, 0, 6, 4, 0],
         [6, 0, 6, 4, 0],
         [0, 5, 1, 6, 7]],
        [[6, 0, 6, 4, 0],
         [0, 5, 1, 6, 7],
         [2, 1, 0, 1, 7]]])

>>color[idx, :].shape

torch.Size([2, 3, 5])

>>color[:, idx]

tensor([[[0, 0, 1],
         [0, 1, 2]],
        [[1, 1, 5],
         [1, 5, 0]],
        [[6, 6, 0],
         [6, 0, 6]],
        [[6, 6, 6],
         [6, 6, 3]]])

>>color[:, idx].shape

torch.Size([4, 2, 3])