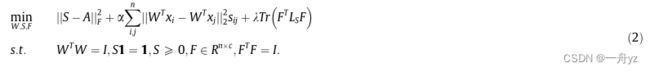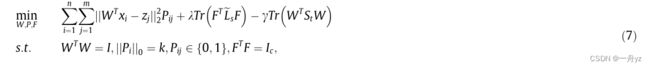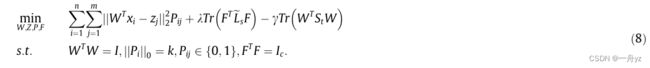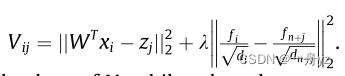Fast unsupervised embedding learning with anchor-based
基于锚图的快速无监督嵌入学习
introduction
一方面,给定一组大量的数据点,所有成对点都有难以处理的关系需要计算。
另一方面,高质量的图在变换矩阵的优化中起着重要作用。原始空间中普遍存在的噪声和冗余特征进一步增加了寻找判别子空间的难度,性能可能会下降。
降维的目标是将数据从高维空间投影到低维空间。在此过程中,去除了噪声和冗余特征,投影数据包含更多的有区别的信息,这对下游任务有指导意义,即探索数据的关系或进行聚类实验。
对于第一个问题,我们直接建立基于锚的图来探索具有锚的数据之间的关系,这可以用稀疏图代替密集图,并降低较高的计算复杂度。针对第二个问题,采用设计良好的算法迭代优化子空间中的变换矩阵和图,可以精确地建模数据点与锚的关系。据我们所知,在将数据分配到适当的簇或类时,缺少数据点的标签也是构建图的分布规律的障碍。
贡献:
- 我们提出了一种快速的无监督嵌入框架,通过在子空间中的数据和锚点之间建立基于锚点的图,可以有效地降低计算复杂度。此外,在子空间中建立并优化了基于锚的图,避免了原始空间中噪声和冗余特征的影响
- 我们将约束拉普拉斯秩加在基于锚的图上,这可以确保没有标签的数据可以精确地划分为c类。我们的模型利用“0范数约束”来避免琐碎的解。
- 提供了一种有效的交替优化算法。实验结果表明,FUAG方法在ACC、NMI和Purity等聚类结果上,以及在时间上,都优于其他无监督降维方法
related work
局部保留投影
局部保持投影(LPP)是一种最具代表性的无监督降维方法,通过保持在原始空间中学习到的局部结构。LPP算法的优化可分为两部分。第一部分是学习数据 X ∈ R d × n X \in R^{d \times n} X∈Rd×n的邻接图 S ∈ R n × n S \in R^{n \times n} S∈Rn×n ,n和d分别是数据的数量和维度。下一个过程是保留相邻结构 S,以确保连接的数据尽可能靠近,以便找到最佳变换矩阵 W ∈ R d × t W \in R^{d \times t} W∈Rd×t 目标函数如下:
I是单位阵 L ∈ R n × n L \in R^{n \times n} L∈Rn×n是拉普拉斯矩阵 L=D-S D是对角矩阵 每个元素是S的每行之和
此外,约束 W T X D X T W W^TXDX^TW WTXDXTW的有效性是去除子空间中的任意比例因子。
即使局部结构可以保留在子空间中,变换矩阵W也将是次优的。由于噪声和冗余特征,相似度矩阵无法准确挖掘数据之间的关系。
基于图优化的无监督投影 UPGO
众所周知,通过上述方法,噪声和冗余特征总是导致次优图 Nie等人提出了一种名为UPGO[21]的迭代算法来优化相似性矩阵,以清晰地探索嵌入数据的局部结构。
原始图 A ∈ R n × n A \in R^{n \times n} A∈Rn×n首先通过KNN或ADP(adaptive graph)方法构造,以保持数据的局部流形结构
一方面,在原始空间中构造相似矩阵A后,UPGO可以通过将相似矩阵 S ∈ R n × n S \in R^{n \times n} S∈Rn×n n在靠近A的子空间中来保留大部分结构信息
另一方面,UPGO自适应地构造优化图来学习投影数据的结构,从而消除噪声的影响
在 S 1 = 1 S \textbf{1}=1 S1=1的约束下构造优化图 此外,为了确保数据可以划分为c个聚类,还对相似矩阵的拉普拉斯矩阵施加了秩约束。目标函数可以定义为
其中A和S是分别学习原始空间和子空间中数据点关系的相似性矩阵
尽管可以精确地探索数据的局部结构,但UPGO的计算复杂度将高达 O ( n 3 ) O(n^3) O(n3),这限制了大规模数据集的应用
methodology
问题描述
数据点的相似性与距离有关,但冗余特征和噪声总是存在于原始空间中,这对数据结构的挖掘有着重要意义,我们在原始数据 X ∈ R d × n X \in R^{d \times n} X∈Rd×n上引入了变换矩阵 W ∈ R d × t W \in R^{d \times t} W∈Rd×t 通过投影数据容易地获得锚定点Z。 Z = [ z 1 , z 2 , … , z m ] ∈ R t × m Z = [z_1,z_2,\dots,z_m] \in R^{t \times m} Z=[z1,z2,…,zm]∈Rt×m其中t和m是子空间中降维和锚点的数目
数据 W T x i W^Tx_i WTxi与锚点 z j z_j zj的距离 ∣ ∣ W T x i − z j ∣ ∣ ||W^Tx_i-z_j|| ∣∣WTxi−zj∣∣越小,成对点之间的相似度Pij越高。然后,可以按照以下问题优化图的相似性
P ∈ R n × m P \in R^{n \times m} P∈Rn×m是相似性矩阵 等式3有平凡解,即每个点的最近锚点的相似性接近1,而其他点的相似度接近0。
为了避免这个问题,我们提出了k-NN图的构造方法。更具体地说,每个数据点仅与k个最近的锚点连接,同时删除与其他锚点的连接。此外,我们对每个点 W T x W^Tx WTx和锚点zj之间的相似性矩阵施加简单的约束,以探索数据的局部结构。
换句话说,Pij=1当且仅当数据点 W T x W^Tx WTx和锚点zj通过边连接。如果没有这样的边,则为Pij=0。因此,P的每一行只有k个元素,其他行为零。
目标函数可以通过“0范数约束”的方式写成如下:
另外,定义矩阵: S = [ P P T ] ∈ R ( n + m ) × ( n + m ) S= \begin{bmatrix} & P \\ P^T & \\ \end{bmatrix} \in R^{(n+m) \times (n+m)} S=[PTP]∈R(n+m)×(n+m)
归一化的拉普拉斯矩阵定义为 L s ~ = I − D − 1 / 2 S D − 1 / 2 \tilde{L_s} = I-D^{-1/2}SD^{-1/2} Ls~=I−D−1/2SD−1/2 D是对角阵每个元素定义为S的行和
定理: 归一化拉普拉斯矩阵 L s ~ \tilde{L_s} Ls~ 的特征值 0 的 重数等于与 S 对应的图中连通分量的数目
然而,考虑到秩的优化很难,我们需要放松秩约束。记 σ i ( L s ~ ) \sigma_i(\tilde{L_s}) σi(Ls~)是 L s ~ \tilde{L_s} Ls~的第i个最小特征值。由于 L s ~ \tilde{L_s} Ls~是正半定的,我们将有 σ i ( L s ~ ) ≥ 0 \sigma_i(\tilde{L_s}) \geq 0 σi(Ls~)≥0对于足够大的 λ \lambda λ,该问题可以转化为以下问题:
根据 Ky Fan’s Theorem 问题等价为:
与秩约束问题相比,问题(6)更容易解决。值得注意的是,我们的模型旨在找到将高维数据嵌入低维空间的变换矩阵W。结合线性判别分析(LDA)中轨迹差异的形式,将不同类中的点分开,模型可表示如下:
其中 γ \gamma γ是控制数据分布的超参数,St是表示所有数据分布的总类散射矩阵。此外,构建的最优图受许多因素的影响,如变换矩阵W和锚点Z。此外,锚点需要进行优化,以适当地拟合数据的分布。考虑到以上所有工作,问题可以改写如下:
模型优化
在我们的模型中,有四个变量变换矩阵W、锚点Z、相似性矩阵P和F。方程(8)可以通过交替优化算法求解迭代更新。
固定P和F:
考虑到锚点Z上没有约束,我们取导数w.r.t Z并将其设置为零。锚点Z可以通过以下等式更新:
定义矩阵 Z ~ ∈ R d × m \tilde{Z}\in R^{d \times m} Z~∈Rd×m 它的第j列可以写为:
将等式(10)代入等式(9),问题(9)可改写如下:
新的数据矩阵 X ~ = [ X Z ~ ] ∈ R d × ( n + m ) \tilde{X}= \begin{bmatrix} X & \tilde{Z} \end{bmatrix} \in R^{d \times(n+m)} X~=[XZ~]∈Rd×(n+m)
L s L_s Ls是S的拉普拉斯矩阵 $S= \begin{bmatrix} & P \ P^T & \ \end{bmatrix} $
显然,等式(12)是一个迹差分问题,变换矩阵W由 X ~ L s X T ~ − γ S t \tilde{X}L_s\tilde{X^T}-\gamma S_t X~LsXT~−γSt对应于t个最小特征值的t个特征向量组成。
固定W和Z 问题8变为:
当F固定时 考虑到每个点是独立的,等式(13)可以重新定义如下:
很明显,Pi 的最优 k 个元素对应于 Vi 的 k 个小值,而 Pi 的其他元素为 0
当P是固定的,并且用 L s ~ \tilde{L_s} Ls~的定义桥接时,等式(13)变成

从等式(15)直接优化F可能容易导致严重的计算复杂性。
F = [ F s F a ] F= \begin{bmatrix} F_s \\ F_a \end{bmatrix} F=[FsFa] D = [ D s D a ] D= \begin{bmatrix} D_s \\ D_a \end{bmatrix} D=[DsDa]
Fs和Fa的最优解由 D s − 1 / 2 P D a − 1 / 2 D_s^{-1/2}PD_a^{-1/2} Ds−1/2PDa−1/2 的前c个左右奇异向量构成
上述问题求解详细过程见论文:
Learning a structured optimal bipartite graph for coclustering