【自动驾驶】16.计算机视觉：相机成像原理：世界坐标系、相机坐标系、图像坐标系、像素坐标系之间的转换

本篇博客为转载，我对其中的细节添加了一些说明。
原文链接：https://blog.csdn.net/chentravelling/article/details/53558096

0.前言

最近整理了“相机成像原理”和“视差与深度信息”相关的资料，然后做成了PPT，以备自己用，也提供给相关的图像、视觉方向的朋友参考。如有误，望海涵并指出。

1.正文

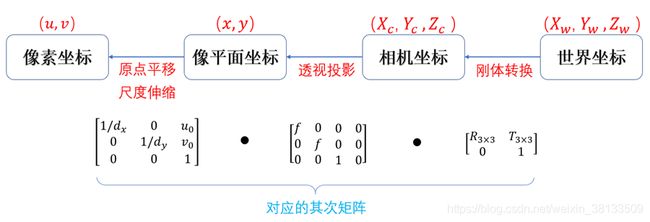
图像处理、立体视觉等等方向常常涉及到四个坐标系：世界坐标系、相机坐标系、图像坐标系、像素坐标系。例如下图：
zhz注：根据右手定则，下面的相机坐标系和世界坐标系的Y轴方向都反了，因为拇指指向X正方向，食指指向Y轴正方向，那么Z轴的正方向就是中指指向。下面的相机坐标系和世界坐标系都是左手坐标系。
构建世界坐标系只是为了更好的描述相机的位置在哪里，在双目视觉中一般将世界坐标系原点定在左相机或者右相机或者二者X轴方向的中点。
接下来的重点，就是关于这几个坐标系的转换。也就是说，一个现实中的物体是如何在图像中成像的。

1.1世界坐标系与相机坐标系

于是，从世界坐标系到相机坐标系，涉及到旋转和平移（其实所有的运动也可以用旋转矩阵和平移向量来描述）。绕着不同的坐标轴旋转不同的角度，得到相应的旋转矩阵，如下图所示：

那么从世界坐标系到相机坐标系的转换关系如下所示：

1.2相机坐标系与图像坐标系

从相机坐标系到图像坐标系，属于透视投影关系，从3D转换到2D。

• p(x,y)是图像坐标系上的点(即相机坐标系上的点投影到图像坐标系的投影点)，o是图像坐标系的中点，也是相机的焦点，f是相机的焦距。
• 相机的成像平面 就是 图像坐标系所在平面(二维平面)。
• P(Xc,Yc,Zc)是相机坐标系上的点，Oc是相机的光心。
  

此时投影点p(x,y)的单位还是mm，并不是pixel，需要进一步转换到像素坐标系。

1.3图像坐标系与像素坐标系

像素坐标系和图像坐标系都在成像平面上，只是各自的原点和度量单位不一样。图像坐标系的原点为相机光轴与成像平面的交点，通常情况下是成像平面的中点或者叫主点(principal point)。

图像坐标系的单位是mm，属于物理单位，而像素坐标系的单位是pixel，我们平常描述一个像素点都是几行几列。

所以这二者之间的转换如下：其中dx和dy表示每一列和每一行分别代表多少mm，即1pixel=dx mm。就是说，
dx就是在水平方向上1个像素的长度(单位mm);
dy就是在竖直方向上1个像素的长度(单位mm)。

p(x,y)是图像坐标系上的点，O(u0,v0)是图像坐标系的中心点，u0,v0对应像素坐标系的u0个pixel 和 v0个pixel，并非mm，如果像素平面的分辨率为W*H (单位pixel)， 那么
$$\begin{gathered} u_0=1/2\ast W \\ {v}_0=1/2\ast H \end{gathered}$$

注意p(x,y)的x,y是从图像坐标系中心点开始的偏移,单位是mm，所以：

• x/dx是从p(x,y)到图像坐标系中心点的横向偏移；
• y/dy是从p(x,y)到图像坐标系中心点的纵向偏移；
• u0,v0为像素坐标系的中心点（不是原点，原点在左上角），等于图片像素的宽和高的一半;
• 图像坐标系 x,y和像素坐标系u,v的量纲单位不一样，x,y是mm, u,v是pixel。

一个点从相机坐标系投影到图像坐标系的点P(x,y)，此时单位还是mm，点p(x,y)的坐标值x，y表示的是距离图像中心点，也是图像坐标系原点的距离(mm)。
由于图像坐标系和像素坐标系就是同一个平面，只是原点不一样。所以点P(x,y)在像素坐标系的坐标就变成了:
$$\begin{gathered} u=\frac{x}{d_x}+u_0 \\ v=\frac{y}{d_y}+v_0 \end{gathered}$$

计算p(x,y)投影到像素坐标系上的值：

那么通过上面四个坐标系的转换就可以得到世界坐标系中的一个点P(Xw,Yw,Zw)如何投影到像素坐标系中的一个点p(u,v)。

前两个矩阵相乘，令fx=f/dx,fy=f/dy,得到的就是上图中标出的相机内参矩阵。其中，fx和fy也叫等效焦距。
相机的内参和外参可以通过张正友标定获取（戳这里查看张正友标定的资料）。

相机内参矩阵K是一个3x3的上三角矩阵。

刚学的小伙伴们可能会有疑问了：为什么上面要把相机内参写成3x4矩阵形式，相机外参写成4x4的形式？
答：是因为在进行代码编程时，并不会使用（R*P+t）这种求法，而且求相反的变换时，涉及到求变换矩阵的逆，而求逆必须是对方阵求逆。所以这里要多加一行$[0_{1\ast 3},1]$。
对于内参矩阵有变成3x4，这里可不必纠结，因为当需要求逆时，我们会把旋转矩阵和平移向量写成齐次矩阵。我们注意看的话，会发现，上面的相机内参3x4其实只有2x3是有效的，其他的都是填充的，并且，里面的3x3已经是齐次了。他这里把相机内参矩阵扩展成3x4只是为了使等式维度吻合，才写成了3x4。实际编程中，只需要把相机内参矩阵取3x3的齐次矩阵，然后再与坐标点进行运算即可。

分析一下这几个空间变换：

如果把物点在相机坐标系下所在的平面叫做物平面。为了描述方便，我们这里以点$(X_C,Y_C,Z_C)$来描述物平面。那么从物平面$(X_C,Y_C,Z_C)$除以$Z_c$变成归一化平面$(X_C/Z_C,Y_C/Z_C,1)$。

相机坐标系 -> 图像坐标系:

$$\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{ccc}f& 0& 0\\ 0& f& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_c/Z_C\\ Y_c/Z_c\\ 1\end{array}\right]$$
这里不是$f_x$和$f_y$，因为这里是相机坐标系到图像坐标系，单位还是mm，并没有变到像素坐标系中。变到像素坐标系中才需要$f$除以$d_x$和$d_y$后变成$f_x$和$f_y$.

---

归一化平面$(\frac{X_C}{Z_C},\frac{Y_C}{Z_C},1)$乘以焦距$f$变为成像平面$(x,y)$。

成像平面$(x,y)$，把长度m和像素直接进行缩放变化，并平移中心点到左上角，就变成像素平面$(u,v)$。

或者直接由归一化平面$(\frac{X_C}{Z_C},\frac{Y_C}{Z_C},1)$乘以相机内参矩阵K，变为像素平面，一步到位。

相机坐标系 -> 像素坐标系:

$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}f/dx& 0& u_0\\ 0& f/dy& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_c/Z_C\\ Y_c/Z_c\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& u_0\\ 0& f_y& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_c/Z_C\\ Y_c/Z_c\\ 1\end{array}\right]$$

---

$Z_c值求解:$

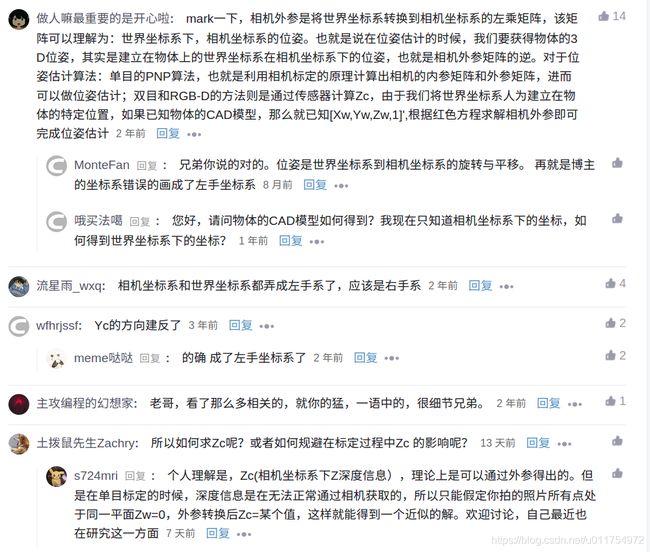
关于$Z_c$值求解，可参考这篇博客：像素坐标转到世界坐标时相机坐标系中的Zc值求解，其中 R为旋转矩阵，K为相机内参矩阵，T为平移向量，均为已知值。$Z_c$是世界坐标系的某点$P(X_w,Y_w,Z_w)$投影到相机坐标系的点的$Z$方向坐标，该博客主要内容如下截图：

对于每个像素$(u,v)$，都有一个对应的$Z_c$,所以，并不是对整张图的像素来说，只有一个$Z_c$。
当我们需要从2D像素点反投影到3D世界坐标系时，只需要知道像素坐标、相机内参、相机外参(即：相机到世界坐标系的旋转矩阵、平移矩阵)，就可以求得这个像素对应的深度$Z_c$，进而可以通过前面的公式：


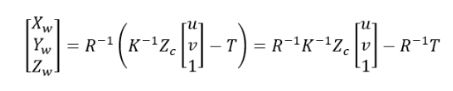
得到该像素对应的三维世界坐标系点。我们在自动驾驶开发项目中，一般会把世界坐标系设定为车身坐标系。对于地面上的车道线等，由于我们知道车身坐标系的原点离地面的高度，就知道了车身坐标系下的$Z_w$，进而可以得到深度信息$Z_c$，从而得到图像中车道线的该像素对应的三维车身坐标系点。

不过，对于高度未知的，就不能求出$Z_c$了。

所以，通过最终的转换关系来看，一个三维中的坐标点，的确可以在图像中找到一个对应的像素点，但是反过来，通过图像中的一个点找到它在三维中对应的点就很成了一个问题，因为我们并不知道等式左边的$Z_c$的值。
关于三维重建不是我的方向，但是深度值的获取是我项目中的一个需要解决的问题，这将涉及到后面的立体视觉知识。

---

上面的公式中省略了去畸变的步骤，该步骤是在使用相机内参矩阵进行变换前，在相机外参矩阵*世界坐标系，得到相机坐标系点(Xc,Yc,Zc)，将其取前两维度除以【Zc】得到二维点(Xc/Zc,Yc/Zc)，见下面公式：

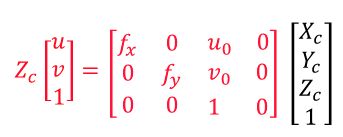
把公式左右两边都除以Zc，然后进行去畸变运算，得到去畸变后的二维点(x,y)，再将去畸变的二维点(x,y)经过【相机内参矩阵】计算，得到最终的像素点坐标(u,v)，即

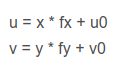
【PPT下载】

地址：http://download.csdn.net/detail/chentravelling/9833120

原文评论截图：

---

---