正则化之L1和L2已经dropout的一些理解和pytorch代码实现与效果证明
文章目录
- 前言
- L1正则化
- L2正则化
- dropout
- 参考
前言
正则化主要解决模型过拟合问题,主要是通过减小w的值,即模型的权重来缓解过拟合的。
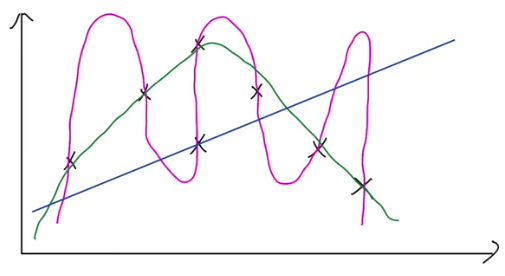
可以看这么一张图,需要一条曲线去拟合图上x的点。
可以看到粉色的线将噪声点都考虑进去了,属于过拟合。
绿色的线能够比较好的拟合点,是我们期望的模型。
蓝色的线是一条直线,没学到什么大小,属于欠拟合
我们使用手写数据集的数据:
链接:https://pan.baidu.com/s/1nxISO_v-MhEyqin7qYqWZw?pwd=1111
提取码:1111
baseline为无正则化:
import pandas as pd
import numpy as np
import torch as th
import torch.nn as nn
import torch.utils.data.dataloader as dataloader
from torch.utils.data import TensorDataset
from tqdm import tqdm
from sklearn.metrics import accuracy_score
def get_dataloader(batch_size, file_name):
filedata = pd.read_csv(file_name, header=None)
label = filedata.values[:, 0]
data = filedata.values[:, 1:]
data = th.from_numpy(data).to(th.float32)
label = th.from_numpy(label).to(th.long) # 标签这里用不到,但是不影响吧
dataset = TensorDataset(data, label)
data_loader = dataloader.DataLoader(dataset=dataset, shuffle=True, batch_size=batch_size)
return data_loader
batch_size = 256
input_size = 784
hidden_size = 20
output_size = 10
learning_rate = 0.001
epoch = 5
test_loader = get_dataloader(batch_size=batch_size, file_name = "mnist_test.csv")
train_loader = get_dataloader(batch_size=batch_size, file_name = "mnist_train.csv")
class network(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super().__init__()
self.input_size = input_size
self.hidden_size = hidden_size
self.output_size = output_size
self.w1 = nn.Linear(input_size, hidden_size, bias=False)
self.w2 = nn.Linear(hidden_size, output_size, bias=False)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
i2h = self.w1(x)
i2h = self.sigmoid(i2h)
h2o = self.w2(i2h)
h2o = self.sigmoid(h2o)
return h2o
def evaluate_model(model, iterator, criterion):
all_pred = []
all_y = []
losses = []
for i, batch in tqdm(enumerate(iterator)):
if th.cuda.is_available():
input = batch[0].cuda()
label = batch[1].type(th.cuda.LongTensor)
else:
input = batch[0]
label = batch[1]
y_pred = model(input)
loss = criterion(y_pred, label)
losses.append(loss.cpu().detach().numpy())
predicted = th.max(y_pred.cpu().data, 1)[1]
all_pred.extend(predicted.numpy())
all_y.extend(label.cpu().detach().numpy())
score = accuracy_score(all_y, np.array(all_pred).flatten())
return score, np.mean(losses)
model = network(input_size=input_size, hidden_size=hidden_size, output_size=output_size)
optimizer = th.optim.Adam(model.parameters(), lr=learning_rate, weight_decay=0.001) # Adam优化器
loss_func = nn.CrossEntropyLoss() # 损失函数
train_scores = []
test_scores = []
train_losses = []
test_losses = []
for epoch in range(epoch):
model.train()
for step, (x, label) in enumerate(train_loader):
regularization_loss = 0
pred = model(x)
loss = loss_func(pred, label) # 损失函数
optimizer.zero_grad() # 清空梯度
loss.backward() # 反向传播
optimizer.step() # 优化器
model.eval()
train_score, train_loss = evaluate_model(model, train_loader, loss_func)
test_score, test_loss = evaluate_model(model, test_loader, loss_func)
train_losses.append(train_loss)
test_losses.append(test_loss)
train_scores.append(train_score)
test_scores.append(test_score)
print('#' * 20)
print('train_acc:{:.4f}'.format(train_score))
print('test_acc:{:.4f}'.format(test_score))
for param in model.parameters():
print(param)
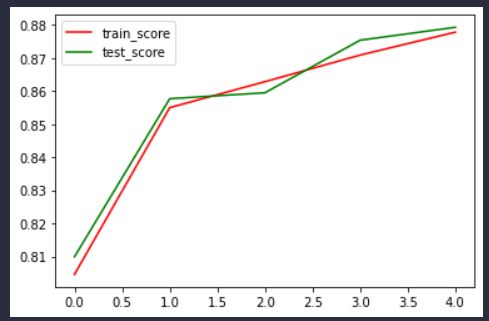
我们可以打印一下模型的参数:
这里重点看最后一组权重,因为数量故意设置的比较少,方便肉眼查看比较:
可以发现模型的参数在[-1, 1]之间
L1正则化
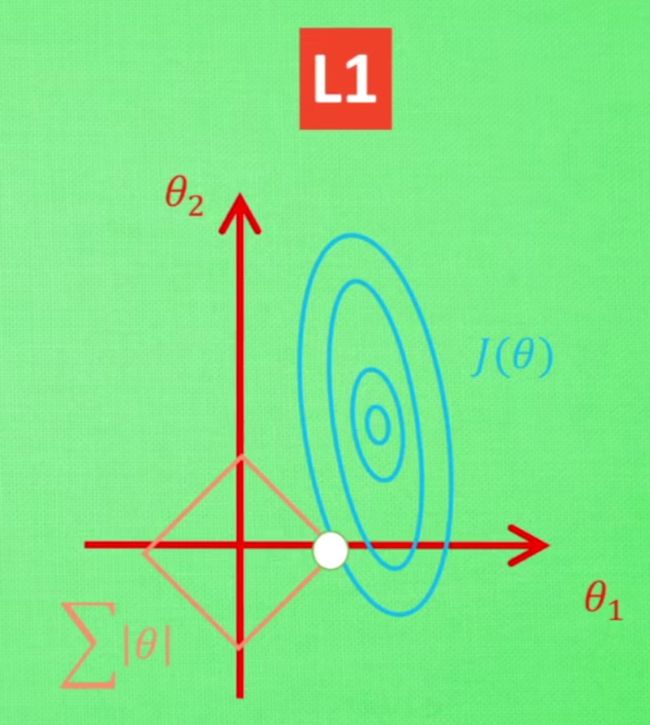
L1正则化是通过增加L1范式来约束权重的。
损失函数表达式如下:
loss(w,b,λ) = loss(w,b) + λ * (|w1| + w2| + … + |wn|)
L1正则化容易使得一些权重为0,因此会起到稀疏化的作用,能够用于特征选择。
在baseline的基础上,我们加上L1正则化
核心代码如下:
model = network(input_size=input_size, hidden_size=hidden_size, output_size=output_size)
optimizer = th.optim.Adam(model.parameters(), lr=learning_rate) # Adam优化器
loss_func = nn.CrossEntropyLoss() # 损失函数
train_scores = []
test_scores = []
train_losses = []
test_losses = []
for epoch in range(epoch):
model.train()
for step, (x, label) in enumerate(train_loader):
regularization_loss = 0
pred = model(x)
loss = loss_func(pred, label) # 损失函数
for param in model.parameters():
regularization_loss += th.sum(th.abs(param))
loss += 0.001 * regularization_loss
optimizer.zero_grad() # 清空梯度
loss.backward() # 反向传播
optimizer.step() # 优化器
model.eval()
train_score, train_loss = evaluate_model(model, train_loader, loss_func)
test_score, test_loss = evaluate_model(model, test_loader, loss_func)
train_losses.append(train_loss)
test_losses.append(test_loss)
train_scores.append(train_score)
test_scores.append(test_score)
print('#' * 20)
print('train_acc:{:.4f}'.format(train_score))
print('test_acc:{:.4f}'.format(test_score))
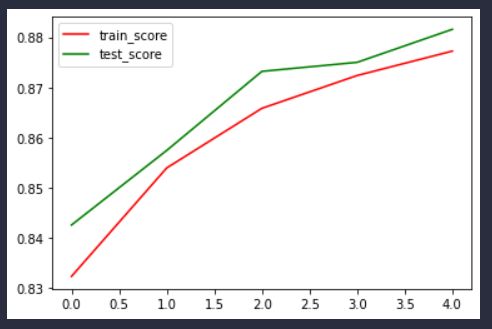
我们可以直观看到模型参数小了很多,并且可以发现几个权重是10-4或者10-5说明这个权重已经很小了,约等于0了,L1的稀疏性也有所体现。
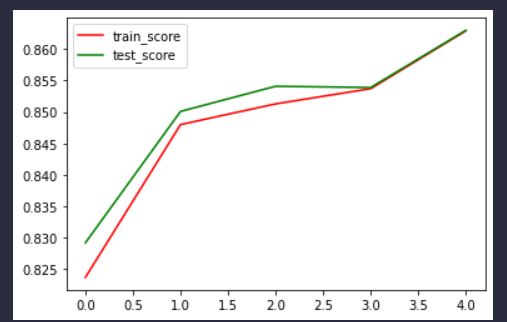
根据训练图像也可以发现,加上L1正则化和,模型的测试集准确率一直好于训练集,的确有助于缓解过拟合现象。
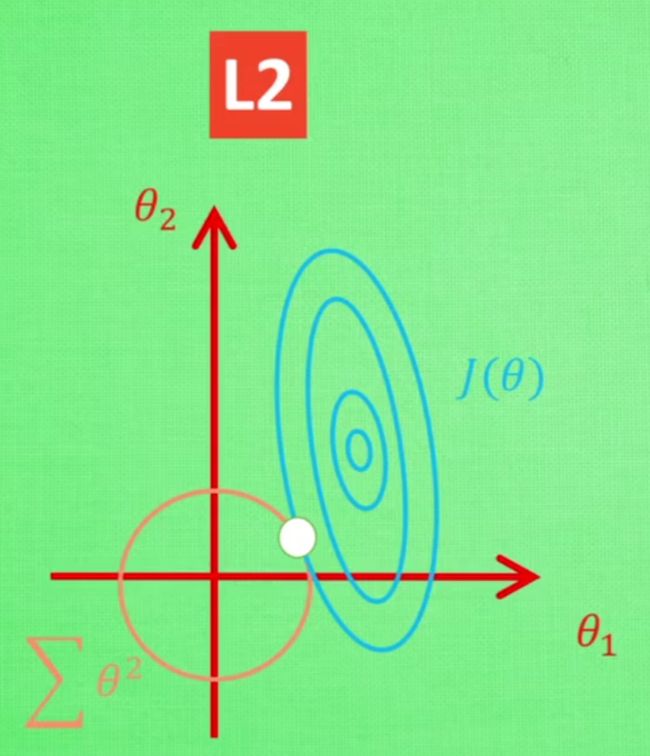
L2正则化
L2正则化就是通过增加L2范式来约束权重。
损失函数表达式如下:
loss(w,b,λ) = loss(w,b) + λ * (w12 + w22 + … + wn2)
在pytorch中L2正则化已经帮我们实现好了
优化器中的weight_decay就是调整L2正则化参数的,默认为0
optimizer = th.optim.Adam(model.parameters(), lr=learning_rate, weight_decay=0.001) # Adam优化器
这样就是使用了L2正则化了
核心代码如下:
model = network(input_size=input_size, hidden_size=hidden_size, output_size=output_size)
optimizer = th.optim.Adam(model.parameters(), lr=learning_rate, weight_decay=0.02) # Adam优化器
loss_func = nn.CrossEntropyLoss() # 损失函数
train_scores = []
test_scores = []
train_losses = []
test_losses = []
for epoch in range(epoch):
model.train()
for step, (x, label) in enumerate(train_loader):
regularization_loss = 0
pred = model(x)
loss = loss_func(pred, label) # 损失函数
optimizer.zero_grad() # 清空梯度
loss.backward() # 反向传播
optimizer.step() # 优化器
model.eval()
train_score, train_loss = evaluate_model(model, train_loader, loss_func)
test_score, test_loss = evaluate_model(model, test_loader, loss_func)
train_losses.append(train_loss)
test_losses.append(test_loss)
train_scores.append(train_score)
test_scores.append(test_score)
print('#' * 20)
print('train_acc:{:.4f}'.format(train_score))
print('test_acc:{:.4f}'.format(test_score))
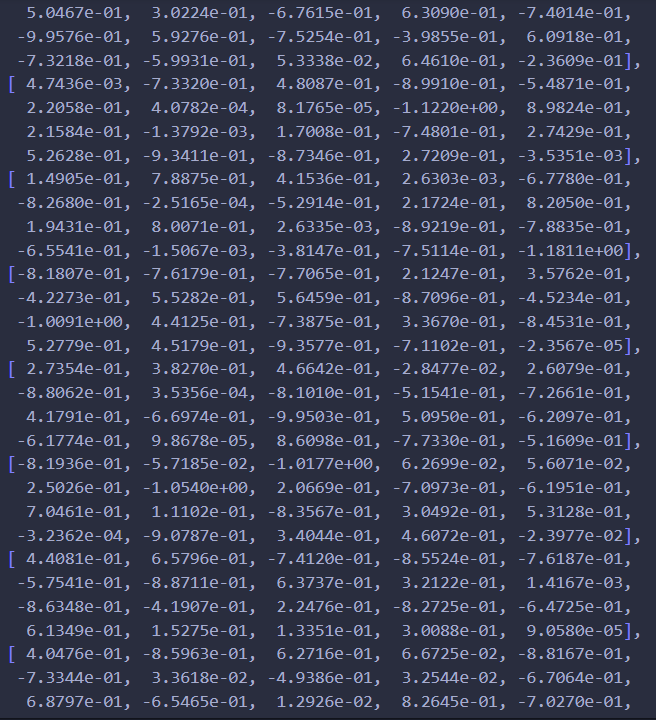
查看模型参数:
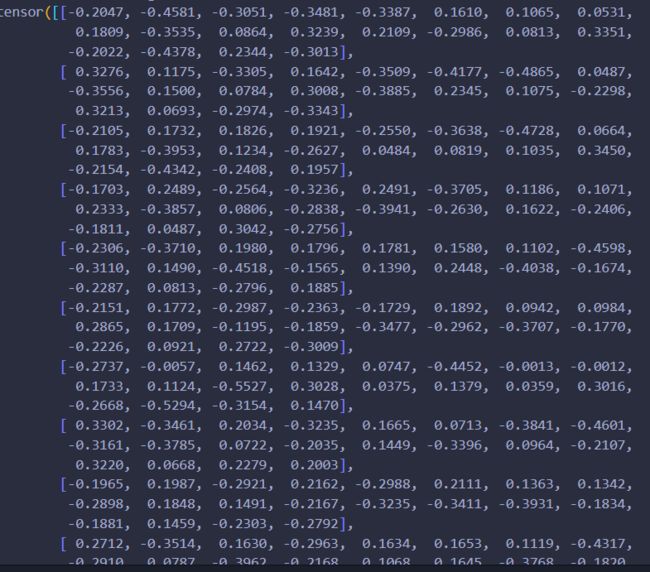
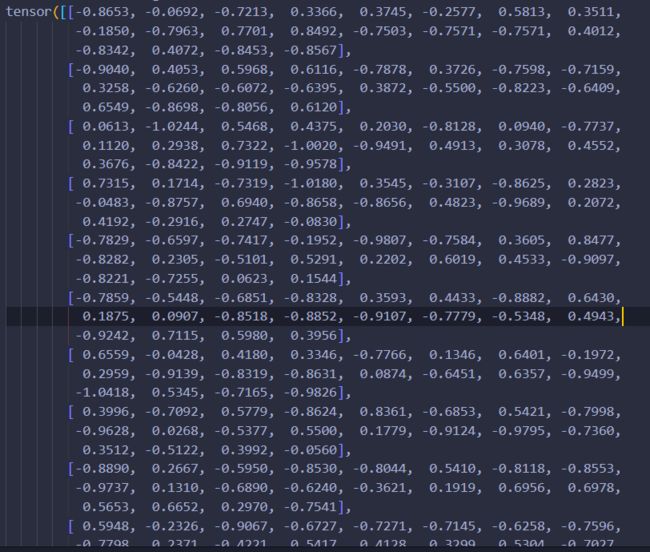
从参数大小上来看,使用了L2正则化,发现最后一组权重都变小了许多,基本上都在0.1-0.4左右,和baseline还是有明显区别的,并且不像L1那样有几个权重特别小。
dropout
dropout是通过随机使一些神经元失效来进行正则化的。
首先dropout能够使一些神经元失效,从而使得模型复杂度降低,从而能够缓解过拟合,
其次,因为dropout随机使得一些神经元失效,那么说明每个神经元并不是时刻有效的,那么就不会被赋予较大的权重,从而达到缓解过拟合的效果。
我们可以看看torch中dropout的效果:
data = th.tensor([1,2,3,5.0])
fc = nn.Linear(4, 10)
dp = nn.Dropout(p=0.5)
res = fc(data)
res_dp = dp(res)
print(res)
print(res_dp)

可以看到,pytorch的dropout就是会随机使一些神经元权重失效(令其=0)然后剩余的神经元扩大,计算公式就为:
剩余原值/(1-p)
核心代码如下:
模型里加个dropout层就行了。
import pandas as pd
import numpy as np
import torch as th
import torch.nn as nn
import torch.utils.data.dataloader as dataloader
from torch.utils.data import TensorDataset
from tqdm import tqdm
from sklearn.metrics import accuracy_score
def get_dataloader(batch_size, file_name):
filedata = pd.read_csv(file_name, header=None)
label = filedata.values[:, 0]
data = filedata.values[:, 1:]
data = th.from_numpy(data).to(th.float32)
label = th.from_numpy(label).to(th.long) # 标签这里用不到,但是不影响吧
dataset = TensorDataset(data, label)
data_loader = dataloader.DataLoader(dataset=dataset, shuffle=True, batch_size=batch_size)
return data_loader
batch_size = 256
input_size = 784
hidden_size = 20
output_size = 10
learning_rate = 0.001
dropout = 0.3
epoch = 5
test_loader = get_dataloader(batch_size=batch_size, file_name = "mnist_test.csv")
train_loader = get_dataloader(batch_size=batch_size, file_name = "mnist_train.csv")
class network(nn.Module):
def __init__(self, input_size, hidden_size, output_size, dropout):
super().__init__()
self.input_size = input_size
self.hidden_size = hidden_size
self.output_size = output_size
self.w1 = nn.Linear(input_size, hidden_size, bias=False)
self.dropout = nn.Dropout(dropout)
self.w2 = nn.Linear(hidden_size, output_size, bias=False)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
i2h = self.w1(x)
i2h = self.sigmoid(i2h)
i2h = self.dropout(i2h)
h2o = self.w2(i2h)
h2o = self.sigmoid(h2o)
return h2o
def evaluate_model(model, iterator, criterion):
all_pred = []
all_y = []
losses = []
for i, batch in tqdm(enumerate(iterator)):
if th.cuda.is_available():
input = batch[0].cuda()
label = batch[1].type(th.cuda.LongTensor)
else:
input = batch[0]
label = batch[1]
y_pred = model(input)
loss = criterion(y_pred, label)
losses.append(loss.cpu().detach().numpy())
predicted = th.max(y_pred.cpu().data, 1)[1]
all_pred.extend(predicted.numpy())
all_y.extend(label.cpu().detach().numpy())
score = accuracy_score(all_y, np.array(all_pred).flatten())
return score, np.mean(losses)
model = network(input_size=input_size, hidden_size=hidden_size, output_size=output_size, dropout=dropout)
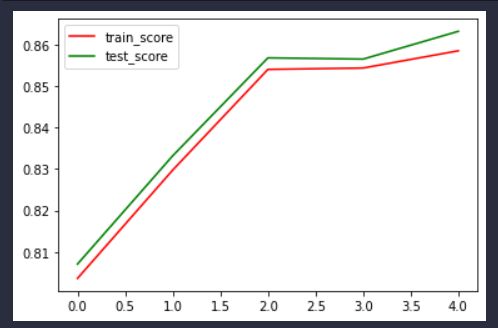
准确率曲线:
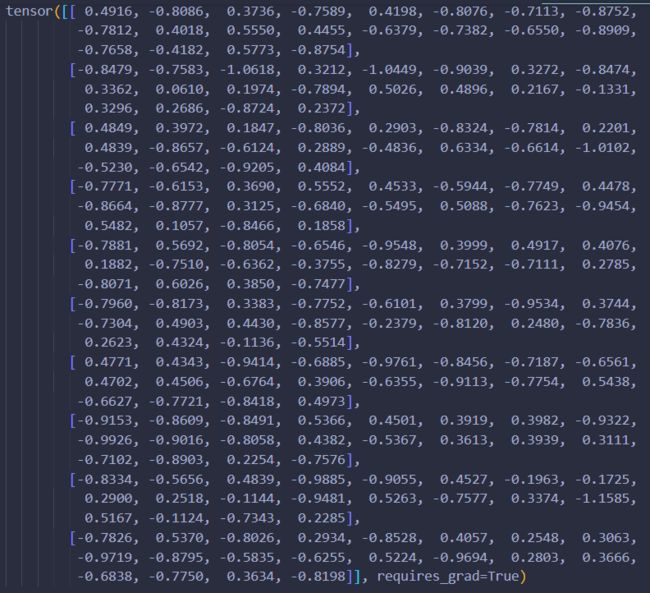
打印最后一层参数:
从训练曲线的角度看,确实有所缓解过拟合现象,因为测试集准确率一直高于训练集,模型的泛化能力较强。
从参数大小方面,就没那么明显了,因为训练次数较少,只有5个epoch而且神经元个数也少,dropout作用其实并不是很大。但是仍然发挥着一定作用。
参考
如何解决过拟合问题?L1、L2正则化及Dropout正则化讲解
什么是 L1 L2 正规化 正则化 Regularization (深度学习 deep learning)