VINS 细节系列 - 特征点三角化

一、原理

在得到运动之后,下一步我们需要用相机的运动估计特征点的空间位置。在单目 SLAM 中,仅通过单张

图像无法获得像素的深度信息,我们需要通过三角测量(Triangulation) 的方法来估计地图点的深度。

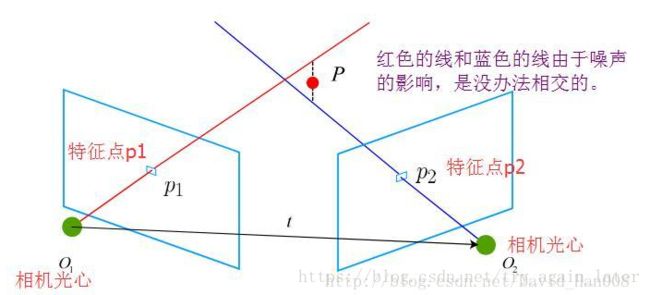
三角测量：通过在两处观察同一个点的夹角，从而确定该点的距离。

设 x 1 , x 2 为两个特征点的归一化坐标,那么它们满足:

 

总结： 根据两帧间的转换关系和两帧中对应的特征点归一化坐标系，求尺度因子 （单目）

具体分析：

理解：

如公式 （2-5） 所示，相邻两个关键帧做三角化，每帧的位姿T和特征点在该帧上的像素坐标可以得到两个约束公式，故相邻两帧便可以得到4个约束公式，下面的程序也是这样写的！

 

 相关论文连接

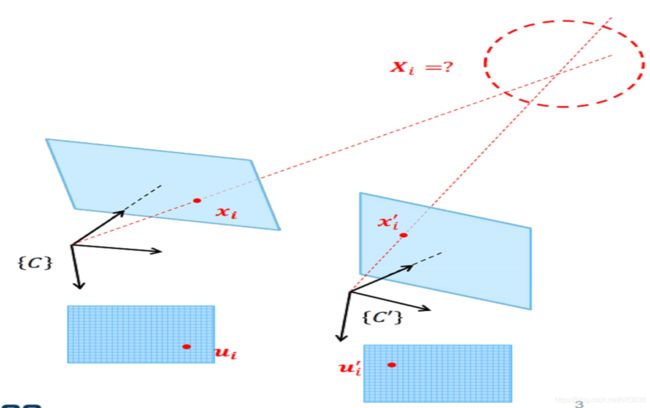
总结： 根据世界坐标系与相机坐标系的转换关系以及特征点的归一化坐标，求特征点世界坐标系下的位置（双目）

二、程序

先介绍上述理论对应的vins-fusion 中的代码，如下：

void FeatureManager::triangulatePoint(Eigen::Matrix &Pose0, Eigen::Matrix &Pose1,
                        Eigen::Vector2d &point0, Eigen::Vector2d &point1, Eigen::Vector3d &point_3d)
{
    Eigen::Matrix4d design_matrix = Eigen::Matrix4d::Zero();
    design_matrix.row(0) = point0[0] * Pose0.row(2) - Pose0.row(0);
    design_matrix.row(1) = point0[1] * Pose0.row(2) - Pose0.row(1);
    design_matrix.row(2) = point1[0] * Pose1.row(2) - Pose1.row(0);
    design_matrix.row(3) = point1[1] * Pose1.row(2) - Pose1.row(1);
    Eigen::Vector4d triangulated_point;
    triangulated_point =
              design_matrix.jacobiSvd(Eigen::ComputeFullV).matrixV().rightCols<1>();
    point_3d(0) = triangulated_point(0) / triangulated_point(3);
    point_3d(1) = triangulated_point(1) / triangulated_point(3);
    point_3d(2) = triangulated_point(2) / triangulated_point(3);
}

 在介绍 VINS-fusion 程序里面对应的代码入口！

if (solver_flag == INITIAL)
    {
        //stereo + IMU initilization，双目初始化
        if(STEREO && USE_IMU)
        {
            f_manager.initFramePoseByPnP(frame_count, Ps, Rs, tic, ric);
            
            //三角化
            f_manager.triangulate(frame_count, Ps, Rs, tic, ric);

void FeatureManager::triangulate()  如下：

我用的是VINS-fusion程序， 里面的单目程序删除了！

void FeatureManager::triangulate(int frameCnt, Vector3d Ps[], Matrix3d Rs[], Vector3d tic[], Matrix3d ric[])
{
    for (auto &it_per_id : feature)
    {
        if (it_per_id.estimated_depth > 0)
            continue;//三角化过的点就不再计算了
      //一、双目
        if(STEREO && it_per_id.feature_per_frame[0].is_stereo)
        {
            //R0 t0为第i帧 左相机 坐标系的点 到 世界坐标系点的变换矩阵Rwc
            int imu_i = it_per_id.start_frame;
            Eigen::Matrix leftPose;
            Eigen::Vector3d t0 = Ps[imu_i] + Rs[imu_i] * tic[0];
            Eigen::Matrix3d R0 = Rs[imu_i] * ric[0];//Rw_bk * Rbk_ck = Rw_ck
            
            leftPose.leftCols<3>()  =  R0.transpose();
            leftPose.rightCols<1>() = -R0.transpose() * t0;
            
            //R1 t1为第i帧 右相机 坐标系的点 到 世界坐标系的变换矩阵 
            Eigen::Matrix rightPose;
            Eigen::Vector3d t1 = Ps[imu_i] + Rs[imu_i] * tic[1];
            Eigen::Matrix3d R1 = Rs[imu_i] * ric[1];
            rightPose.leftCols<3>() = R1.transpose();
            rightPose.rightCols<1>() = -R1.transpose() * t1;
             
            //左 右 相机的归一化坐标
            Eigen::Vector2d point0, point1;
            Eigen::Vector3d point3d;
            point0 = it_per_id.feature_per_frame[0].point.head(2);
            point1 = it_per_id.feature_per_frame[0].pointRight.head(2);
          
          //理论部分：相机坐标系与世界坐标系的转换关系 + 归一化坐标 + 通过公式 = 世界坐标系下的3D点
            triangulatePoint(leftPose, rightPose, point0, point1, point3d);
            
          //世界坐标系的3D点，转换到相机坐标系，z便是深度！ 体会这个意思
            Eigen::Vector3d localPoint;
            localPoint = leftPose.leftCols<3>() * point3d + leftPose.rightCols<1>();
            
            double depth = localPoint.z();
            if (depth > 0)
                it_per_id.estimated_depth = depth;
            else
                it_per_id.estimated_depth = INIT_DEPTH;
      
            continue;
        }//到此，滑窗内所有特征点的深度求出来了
        

       //二、单目部分
        it_per_id.used_num = it_per_id.feature_per_frame.size();
        if (it_per_id.used_num < 4)
            continue;

        int imu_i = it_per_id.start_frame, imu_j = imu_i - 1;

        Eigen::MatrixXd svd_A(2 * it_per_id.feature_per_frame.size(), 4);
        int svd_idx = 0;

        Eigen::Matrix P0;
        Eigen::Vector3d t0 = Ps[imu_i] + Rs[imu_i] * tic[0];
        Eigen::Matrix3d R0 = Rs[imu_i] * ric[0];
        P0.leftCols<3>() = Eigen::Matrix3d::Identity();
        P0.rightCols<1>() = Eigen::Vector3d::Zero();

        for (auto &it_per_frame : it_per_id.feature_per_frame)//遍历
        {
            imu_j++;
            //R t为第j帧相机坐标系到第i帧相机坐标系的变换矩阵，P为i到j的变换矩阵
            Eigen::Vector3d t1 = Ps[imu_j] + Rs[imu_j] * tic[0];
            Eigen::Matrix3d R1 = Rs[imu_j] * ric[0];
            Eigen::Vector3d t = R0.transpose() * (t1 - t0);
            Eigen::Matrix3d R = R0.transpose() * R1;
            
            
            Eigen::Matrix P;
            P.leftCols<3>() = R.transpose();
            P.rightCols<1>() = -R.transpose() * t;
            
            Eigen::Vector3d f = it_per_frame.point.normalized();
            svd_A.row(svd_idx++) = f[0] * P.row(2) - f[2] * P.row(0);
            svd_A.row(svd_idx++) = f[1] * P.row(2) - f[2] * P.row(1);

            if (imu_i == imu_j)
                continue;
        }
        
        //对A的SVD分解得到其最小奇异值对应的单位奇异向量(x,y,z,w)，深度为z/w
        ROS_ASSERT(svd_idx == svd_A.rows());
        Eigen::Vector4d svd_V = Eigen::JacobiSVD(svd_A, Eigen::ComputeThinV).matrixV().rightCols<1>();
        
        double svd_method = svd_V[2] / svd_V[3];
 
        it_per_id.estimated_depth = svd_method;
        
        if (it_per_id.estimated_depth < 0.1)
        {
            it_per_id.estimated_depth = INIT_DEPTH;
        }

    }
}

疑问：为什么  “一、双目”  后面还会有“二、单目”，程序是不是错了！

答：不是的，我看的这个程序是VINS-fusion,  包括双目，单目程序，而我最近在研究双目的程序，故出现这样的情况；

再者，读取文件满足双目情况时，程序是不进入下面的单目的，因为双目中的 continue  存在的原因，遇到 continue 就会返回

for 循环重新开始，直到没有特征点，整个程序不再运行，自己看程序体会一下！

三、总结

1、纯旋转无法使用三角测量，由于对极约束永远满足，需要有平移,平移较大时，三角化测量将更精确。

2、多视几何的公式推导中，多次使用"共线向量叉乘等于0"的性质; 另一个常用的性质是"互相垂直的两个向量点乘为零";

程序读了很多遍，感觉每次都有收获，努力把这个程序完全搞懂！