word2vec

1. word2vec简述

以前我们使用一些字符进行机器学习时，时常采用的是先对字符数据进行 $One-hot$ 编码，再将编码后的数据转为矩阵进行输入，这样，语言数据就成为了数字数据，能够进行更新与训练。但是，这种方法有很大的缺点，最明显的缺点就是所占用的空间太过庞大。想想，如果我们需要将英文单词输入我们构建的模型中，这样就需要对每个英文单词进行 $One-hot$ 编码，而每个单词的编码维度就与单词数量有关，如果有五万个单词，那么每个单词的 $One-hot$ 编码维度都是 $50000\times 1$，这会占用极大的空间。

所以，我们可以换一种方法来对类似单词等输入进行表示，例如——词向量。词向量在NLP的深度学习中占有十分重要的地位。理想情况下，存在这么一个维度，每一个单词都在这个维度里可以表示，且意思相近的单词距离近，意思相差较远的单词距离较远，基于此，我们可以将词语映射到一个比 $One-hot$ 编码维度更低的维度，降低空间的占用，$word2vec$ 就是这样一种将单词转为向量的情况。

实现 $word2vec$ 的算法一般由两种，一种是 $skip-gram$ 算法，一种是 $CBOW$ 算法，接下来我将对这两种算法进行一些介绍和实现。

2. Skip-gram算法

2.1 Skip-gram 介绍

$Skip-gram$ 算法实际上是根据一个中心词来预测上下文的词。比如有如下一句话
$$Knowledgemakeshumble,ignorancemakesproud.$$假设我们选择窗口大小 $skip\_window=2$，且中心词是 $humble$，那么我们要做的就是根据中心词来对上文两个单词以及下文两个单词进行预测，用条件概率公式可以表示为：
$$P(Knowledge,makes,ignorance,makes|makes)$$在这里，我们再假设每个单词之间是独立分布的，于是要求的概率可以变为：
$$P(Knowledge|makes)P(makes|makes)P(ignorance|makes)P(makes|makes)$$虽然以人来说用一个单词预测上下文两个单词有点扯，但是对计算机而言这只是个概率与学习的问题，所以完全是可行的。

原论文中的图示如下：

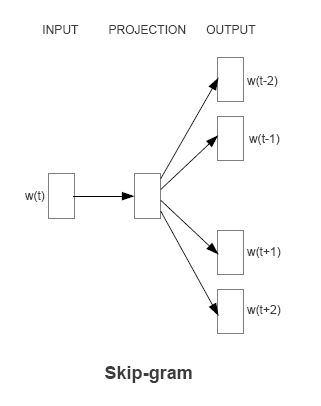
2.2 Skip-gram 步骤

$Skip-gram$ 的结构如下图所示

1. 首先，我们会用 $One-hot$ 向量表示中心词来作为输入，长度为 $V$ 的一维向量。
2. 接着我们会遇到一个大小为 $V\times n$ 的矩阵，也就是矩阵 $W_{V\times N}$（中心词矩阵），这里的 $n$ 就是我们想要得到的词向量的维度，实际上我们想要得到的也就是这个 $W_{V\times N}$
3. 将他们两相乘后我们可以得到一个 $n$ 维的向量，这就是隐藏层
4. 接着我们会遇到一个大小为 $V\times n$ 的矩阵，但是这次是矩阵 $W_{V\times N}^{\prime }$（上下文矩阵）
5. 将他们两相乘后我们可以得到一个 $V$ 维向量，我们可以将这个向量看成 $V$ 个数，对应词库中的 $V$ 个词
6. 对这 $V$ 个数做 $softmax$ 归一化处理，概率最大的那个词所对应的词即为模型所预测的词
7. 若模型预测的词与上下文的词不符，我们会使用反向传播算法来修正权重向量 $W$ 和 $W^{\prime }$。

2.3 参数更新

设中心词为 $w_c$，要预测的词为 $w_0$，中心词矩阵 $W_{V\times N}$ 对应的行为 $v_c$，上下文矩阵 $W_{V\times N}^{\prime }$ 对应的行为 $u_0$，最后经过 $softmax$ 层后的预测概率可以表示为
$$P(w_0|w_c)=\frac{e^{u_0^T{v}_c}}{{\sum }_i{e}^{u_i^T{v}_c}}$$由此我们可以得到每个词作为中心词时推断出两边的词的概率如下所示：
$$\prod _{t=1}^T\prod _{-m<j<m,j\ne 0}P(w^{t+j}|w^t)$$基于该方法，我们可以使用最大似然法，转化为对该函数的对数求最小值，如下所示
$$\begin{array}{rl}min& =-\sum _{t=1}^T\sum _{-m<j<m,j\ne 0}\log P(w^{t+j}|w^t)\end{array}$$以 $P(w_0|w_c)$ 为例，我们还可以将式子 $P(w_0|w_c)$ 带入得到：
$$\log P(w_0|w_c)=u_0^T{v}_c-\log (\sum _i{e}^{u_i^T{v}_c})$$到了这一步，已经能够使用矩阵的求导法则对 $u_0$ 以及 $v_c$ 进行求导，并负梯度下降更新参数了，这也就达到了参数更新的目的，使词嵌入模型训练出来。比如，更新中心词矩阵时，更新的公式如下：
$$\begin{array}{rl}{v}_c& =v_c-\alpha \ast \nabla P(w_0|w_c)\\ & \\ \nabla P(w_0|w_c)& =u_0-\sum _{c-m<j<c+m,j\ne c}\frac{e^{u_0^T{v}_c}}{{\sum }_i{e}^{u_i^T{v}_c}}{u}_j\end{array}$$

3. CBOW算法

$CBOW$ 算法的结构图如下所示

简单来说， $CBOW$ 就是以上下文的窗口词来对中心词进行预测，与前面介绍的 $Skip-gram$ 恰好相反，但是算法的具体步骤还是相差不多的，这里也就不对其进行二次述说了。

4. 两者对比

• $CBOW$ 预测行为的次数跟整个文本的词数几乎是相等的（每次预测行为才会进行一次反向传播, 而往往这也是最耗时的部分），复杂度大概是 $O(V)$；

• $Skip-gram$ 进行预测的次数是要多于 $CBOW$ 的：因为每个词在作为中心词时，都要使用周围词进行预测一次。这样相当于比 $CBOW$ 的方法多进行了 $K$ 次（假设K为窗口大小），因此时间的复杂度为 $O(KV)$，训练时间要比 $CBOW$ 要长。

• 在 $Skip-gram$ 当中，每个词都要收到周围的词的影响，每个词在作为中心词的时候，都要进行 $K$ 次的预测、调整。因此， 当数据量较少，或者词为生僻词出现次数较少时， 这种多次的调整会使得词向量相对的更加准确。

• $CBOW$ 中，某个词也是会受到多次周围词的影响（多次将其包含在内的窗口移动），进行词向量的跳帧，但是他的调整是跟周围的词一起调整的，梯度的值会平均分到该词上， 相当于该生僻词没有收到专门的训练，它只是沾了周围词的光而已。

5. 算法改进

5.1 二次采样

在一个很大的语料库中，有一些很高频率的一些词（比如冠词 a,the ；介词 in，on等）。

这些词相比于一些出现的次数较少的词，提供的信息不多。同时这些词会导致我们很多的训练是没有什么作用的。

为了缓解这个问题，提出了二次采样的思路：每一个单词都有一定概率被丢弃。这个概率为：
$$P(w_i)=1-\sqrt{\frac{t}{f(w_i)}}$$$f(w_i)$ 是单词出现的次数与总单词个数的比值。（例如 $peanut$ 在 $1billion$ 单词语料中出现了 $1000$ 次，那么$z(peanut)=1E-6$）

$t$ 是一个选定的阈值，一般在 $1E-5$ 左右。

5.2 负采样

在训练模型参数时，每接受一个训练样本，就需要调整所有神经单元权重参数，来使神经网络预测更加准确。比如说，以上面的中心矩阵的更新为例，更新公式如下：
$$\begin{array}{rl}\nabla P(w_0|w_c)& =u_0-\sum _{c-m<j<c+m,j\ne c}\frac{e^{u_0^T{v}_c}}{{\sum }_i{e}^{u_i^T{v}_c}}{u}_j\end{array}$$这里的 ${\sum }_i{e}^{u_i^T{v}_c}$ 计算量将会十分大，为所有单元的权重参数，即每个训练样本都将会调整所有神经网络中的参数。

负采样的思路很简单，不直接让模型从整个词表中找最可能的词，而是直接给定这个词（正例）和几个随机采样的噪声词（负例），然后模型能够从这几个词中找到正确的词，就算达到目的了。在论文中作者指出指出对于小规模数据集，建议选择 5-20 个负样本，对于大规模数据集选择 2-5个负样本。

5.2.1 负采样计算

我们依旧以上述的 $P(w_0|w_c)$ 为例，我们选取 $m$ 个负采样，将负样本与正样本当做全部的样本，于是根据极大似然估计可以
$$\begin{array}{rl}\log P(w_0|w_c)& =\log [P(w_0|w_c)\cdot \prod _{i=1}^{m}P(w_i|w_0)]\end{array}$$我们可以知道，其实最大的复杂度来自于最后一层的 $softmax$ 层的计算，所以为了减小 $softmax$ 层的复杂度，选取使用 $sigmoid$ 层来代替 $softmax$ ，以 $sigmoid$ 输出的值近似每一个词的输出概率，所以可以得到：
$$\begin{array}{rl}\log P(w_0|w_c)& =\log [\sigma (u_0^T{v}_c)\cdot \prod _{i=1}^m\sigma (u_i^T{v}_c)]\\ & =\log \sigma (u_0^T{v}_c)+\log [\prod _{i=1}^m\sigma (u_i^T{v}_c)]\\ & =\log (\frac{1}{1+e^{u_0^T{v}_c}})+\sum _{i=1}^m\log (\frac{1}{1+e^{u_i^T{v}_c}})\end{array}$$

5.2.2 负样本的选择

论文中使用 一元模型分布来选择负样本。

一个单词被选作负样本的概率跟它出现的频次有关，出现频次越高的单词越容易被选作负样本，经验公式为：
$$P(w_i)=\frac{f(w_i{)}^{3/4}}{{\sum }_{j=0}^n(f(w_j{)}^{3/4})}$$ $f(w)$ 代表 每个单词被赋予的一个权重，即它单词出现的词频,分母代表所有单词的权重和，公式中指数3/4完全是基于经验的，论文中提到这个公式的效果要比其它公式更加出色。