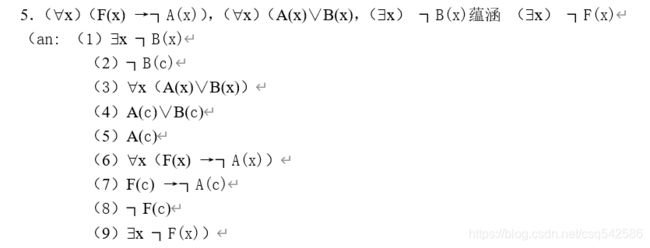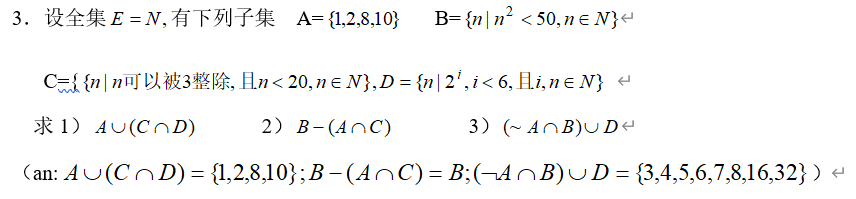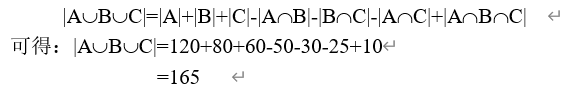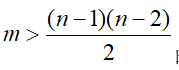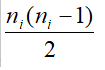*加精*离散数学期末考试复习预测题一（内附详细解析）
离散数学期末考试复习预测题
目录
离散数学期末考试复习预测题
第一章命题逻辑
第二章谓词逻辑
第三章集合论
离散数学复习提纲（代数系统）
离散数学复习提纲（图论）
第一章命题逻辑
4．┐Q
（P→Q）蕴涵 ┐P
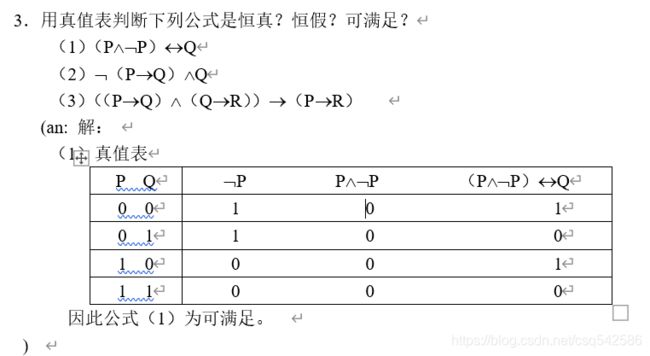
（an: 法1：真值表
法2：若┐Q
（P→Q）为真，则 ┐Q，P→Q为真，
所以Q为假，P为假，所以┐P为真。
法3：若┐P为假，则P为真，再分二种情况：
①若Q为真，则┐Q
（P→Q）为假
②若Q为假，则P→Q为假，则┐Q
（P→Q）为假
根据① ②，所以 ┐Q
（P→Q）蕴涵 ┐P。）
6．用形式演绎法证明：
蕴涵
第二章谓词逻辑
1．设个体域D=
消去
2．所有的主持人都很有风度。李明是个学生并且是个节目主持人。因此有些学生是很有风度。请用谓词逻辑中的推理理论证明上述推理。（个体域：所有人的集合）
6．符号化下列命题并推证其结论：
没有不守信用的人是可以信赖的，有些可以信赖的人是受过教育的人，因此，有些受过教育的人是可守信用的。（个体域：所有人的集合）
（an:
令M(x)：x是守信用的；J(x)：x是受过教育的；D(x)：x是可以信赖的
7．在一阶逻辑中，构造下面的证明：前提：
第三章集合论
1．设〈A，
〉是偏序集，A={1，2，3，4，5，6，8}，是整除关系，请画出〈A，的哈斯图。写出A中的极大元，极小元和最大元，最小元。
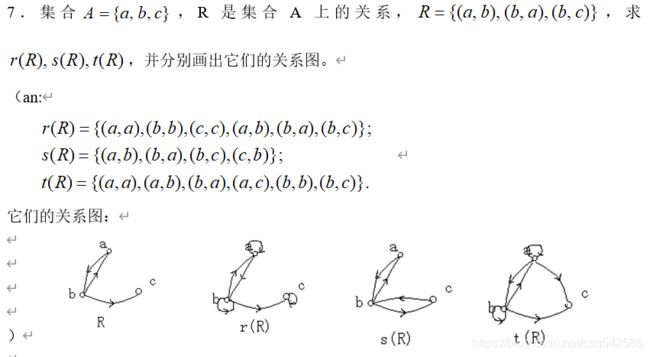
2．设A={1，2，3}，求A上所有等价关系。
5．一个年级170人中，120名学生学英语，80名学生学德语，60名学生学日语，50名学生既学英语又学德语，25名学生既学英语又学日语，30名学生既学德语又学日语，还有10名学生同时学习三种语言。试问：有多少名学生这三种语言都没有学习？
（an: 解：
设E为全集，A为学英语学生的集合，B为学德语学生的集合，C为学日语学生的集合。由公式，
所以，这三种语言都没有学习的学生为 170-165=5人。）
设集合
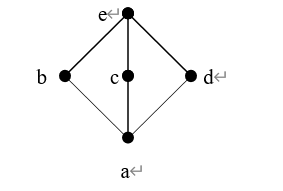
试画出偏序集
的哈斯图，并写出A的最大元，最小元，极大元和极小元。
（an: （A，
）的哈斯图为：
a为A的极小元，也是最小元；
e为A的极大元，也是最大元。
）
离散数学复习提纲（代数系统）
1．（1） 相等关系显然是所有代数结构上的同余关系. 同余关系是相等关系的推广。
（2） 同余关系也是模k相等关系（数论中也称模k同余关系）的推广。可证模k相等关系是如上定义的关于整数加、乘运算的同余关系。
设整数x,y,u,v满足x＝y（mod k）, u＝v（mod k）,
那么x – y = nk,u – v = mk(n,m为整数),于是
(x+u) – (y+v) = (n+m)k
故x+u = y+v（mod k）。
为证 xu＝yv（mod k），将 x = y+nk与u = v+mk两边分别相乘,于是有
xu – yv = ymk+vnk+nmk2
xu – yv = (ym+vn+nmk)k
由于ym+vn+nmk 为整数，xu＝yv（mod k）得证。
模k相等关系关于减运算和一元减运算（添负号运算）也是同余关系，请读者自行验证。
2．设
证 先证充分性．
设 ak ＝ e，k整除n，那么n = kr（r为整数），因为ak ＝ e，所以an = akr = (ak )r = e r = e 。
再证必要性．
设 an ＝ e，n = mk＋ r，其中m为n除以 k的商，r为余数，因此0≤ r＜k 。于是
e＝an＝amk+r＝amk*ar＝ar
因此,由k的最小性得r = 0，k整除n ．
3．有限群G的每个元素都有有限阶,且其阶数不超过群G的阶数 | G | .
证 设a为G的任一元素,考虑 e = a0 ,a1 ,a2 , … ,a│G│
这 | G |+1个G中元素.由于G中只有 | G |个元素,因此它们中至少有两个是同一元素,不妨设
ar = as (0 ≤ r < s ≤ | G | )
于是as-r = e,因此a有有限阶,且其阶数至多是s-r,不超过群G的阶数| G | .
4．设
证 只要证 a具有阶n当且仅当a-1具有阶n 。由于逆元是相互的，即(a-1)-1＝a，同此只需证：当a具有阶n时，a-1 也具有阶n 。
设a的阶是n，a-1的阶是m 。由于(a-1)n＝(an)-1＝e -1＝ e
故m≤n 。又因为a m＝((a-1)m)-1＝ e -1＝ e
故n≤m 。因此，n＝m 。
5．设
（l）G的么元eÎH ．
（2）若a，bÎH ，则a*bÎH ．
（3）若aÎH，则a-1ÎH．
证 先证必要性．
设H为子群．那么（2）是显然的（因H为子代数）．为证（l）,设
充分性是明显的.事实上只要条件（2），（3）便可使
显然,对任何群G , <{e}，*>及
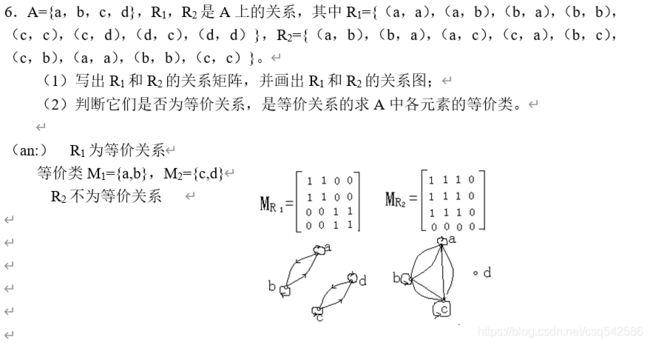
6． （1）
（2）令 A ={2i | iÎI}，那么(·为数乘 )是循环群 ，2是生成元．
（3）
7．循环群的子群都是循环群．
证 设
（1）若H＝{e},显然H为循环群．
（2）若H¹{e}，那么H中有gi(i¹0)．由于H为子群，H中必还有g-i .因此，不失一般性，可设i为正整数，并且它是H中元素的最小正整数指数．现证H为gi生成的循环群．
设gj为H中任一元素．令j＝mi+r，其中m为i除j的商，r为剩余，0≤r＜i．于是
gj = gmi+r＝gmi*gr
gr= g-mi*gj
由于gj, g-miÎH，（因gmiÎH），故grÎH，根据i的最小性，r＝ 0，从而 gj = gmi = (gi)m， H为循环群
8．（1）
<{0}, ＋> ，<{0,2,-2,4,-4 ,…}, ＋> ，<{0,3,-3,6,-6, …}, ＋> ，
<{0,4,-4,8,-8, …}, ＋>,
（2）
<{0}, ＋6 > ，<{0,2,4},＋6> ，<{0,3},＋6> ,
离散数学复习提纲（图论）
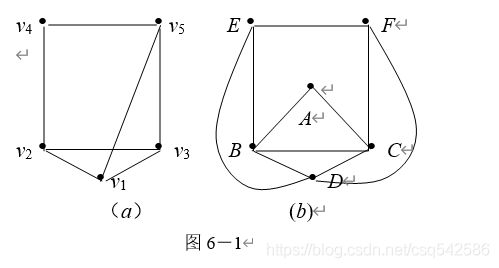
1. 判别图6－1的两幅图是否可以一笔画出？
解 在图6－1(a) 中，
deg(v1)=deg(v2)=deg(v3)＝3
有两个以上的结点的度为3. 故在(a)中不存在欧拉通路，不能一笔画出.
在图6－1(b) 中，deg(A)=2, deg(B) =deg(C)= deg(D)=4，deg(E) =deg(F)=3
只有两个奇数度的结点，所以存在欧拉通路，可以一笔画出. 一条欧拉通路，如EDBEFCABCDF.
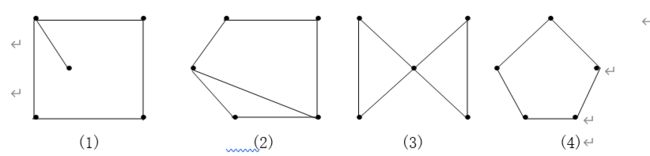
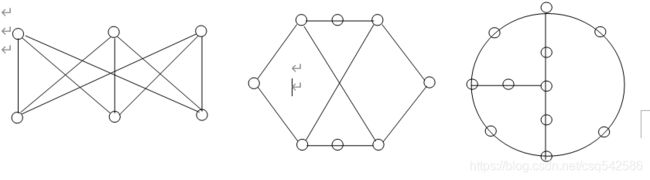
2． 画出具有下列条件的有5个结点的无向图.
- 不是哈密顿图，也不是欧拉图；
(2) 有哈密顿回路，没有欧拉回路；
(3) 没有哈密顿回路，有欧拉回路；
(4) 是哈密顿图，也是欧拉图.
解 作图如图6－3(不唯一).
在图(1)中，可以走遍5个点，但不是回路，无哈密顿回路，故不是哈密顿图。无论指定怎样的方向，可以走遍所有边，但不是回路，不能构成欧拉路。
在图(2)中，容易找出走遍5个点的回路，即有哈密顿回路，故是哈密顿图。但是构成回路，要么出现重复边，要么漏掉边，即不存在欧拉回路，因此不是欧拉图。
在图(3)中，不重复地走遍5个点是不可能的，故不是哈密顿图。如指定右边垂直边方向向上，就可以画出一个走遍所有的边，又不重复的回路，所以有欧拉回路，故是哈欧拉图。
在图(4)中 ，满足要求的条件是显然的。
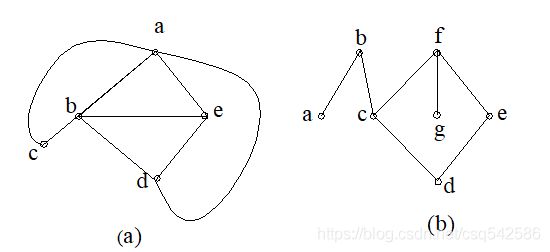
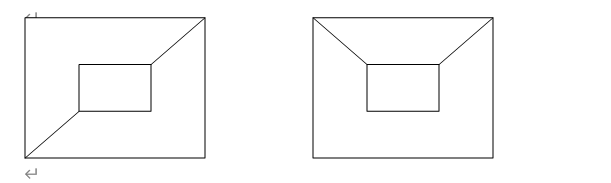
3．在下列图中各有几个面，写出每个面的边界和次数。
解：（a）图中共有5个面。
第1个面，边界为a b e a，次数为3；第2个面，边界为b d e b，次数为3；
第3个面，边界为a b c a，次数为3；第4个面，边界为a d e a，次数为3；
第5个面，边界为a c b d a，次数为4。
（b）图中共有两个面，第1个面，边界为 g f c d e f g，次数为6；
第2个面，边界为 a b c d e f c b a，次数为8。
4．在具有n个结点的完全图Kn中，需要删去多少条边才能得到树？
解 n个结点的完全图共有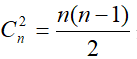
条边，而n个结点的树共有n－1条边. 因此需要删去
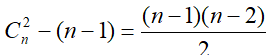条边后方可得到树。
5．设G是图，无回路，但若外加任意一条边于G后，就形成一回路. 试证明G必为树.
证明 由树的定义可知，只需证G连通即可. 任取不相邻两点u,v, 由题设，加上边<u,v>就形成一回路，于是去掉边<u,v>,从u到v仍有路u,…,v，即u,v连通，由u,v的任意性可知，G是连通的，故G必是树.
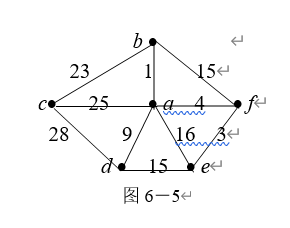
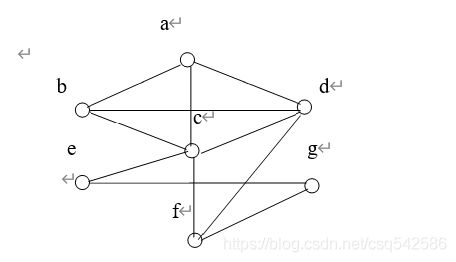
6．如图6－5是有6个结点a,b,c,d,e,f
的带权无向图，各边的权如图所示. 试求
其最小生成树
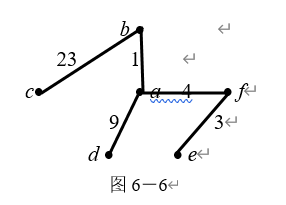
解 构造连通无圈的图，即最小生成树，
用克鲁斯克尔算法：
第一步： 取ab＝1；第二步： 取af=4；第三步： 取fe=3；第四步： 取ad=9；
第五步： 取bc=23.
如图6－6。权为1+4+3+9+23=30
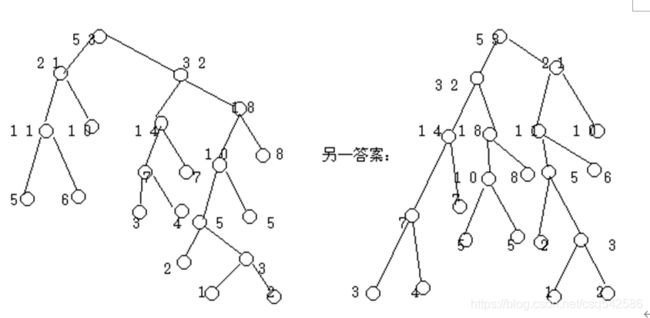
7．试画出一棵带权1，2，2，3，4，5，5，6，7，8，10的最优二叉树。
解：最优二叉树如下：
9．试证明下图中两个无向图是不同构的。
10．一个简单无向图同构于它的补图，称为自补图，证明其结点必是4k或者4k+1.
11．非平凡的树至少有两个叶子。
12．证明: 在任何n (n≥2)个顶点的简单图G中，至少有两个顶点具有相同的度。
证 如果G有两个孤立顶点，那么它们便是具有相同的度的两个顶点。
如果G恰有一个孤立顶点，那么我们可对有n – 1 个顶点但没有孤立顶点的G’（它由G删除孤立顶点后得到）作下列讨论。
不妨设G没有孤立顶点，那么G 的n个顶点的度数应是：1，2，3，…，n–1 这n–1种
可能之一，因此必定有两个顶点具有相同的度。
13．n个城市间有m条相互连接的直达公路。证明：当
时，人们便能通过这些公路在任何两个城市间旅行。
证 用n个顶点表示n个城市，顶点间的边表示直达公路，据题意需证这n个城市的公路网络所构成的图G是连通的。反设G不连通，那么可设G由两个不相关的子图（没有任何边关联分别在两个子图中的顶点）G1，G2组成，分别有n1，n2个顶点，从而，n = n1+n2，n1 ≥1，n2 ≥1。
由于各子图的边数不超过
，因此G的边数m满足：
14．有7人a，b，c，d，e，f，g分别精通下列语言，问他们7人是否可以自由交谈（必要时借助他人作翻译）。
a 精通英语。
b 精通汉语和英语。
c 精通英语、俄语和意大利语。
d 精通日语和英语。
e 精通德语和意大利语。
f 精通法语、日语和俄语。
g 精通法语和德语。
解 下图中7个顶点表示7个人，关联两个顶点的边表示两个人同时精通某一种语言：
由于该图是连通的，因此他们7人是可以自由交谈（必要时借助他人作翻译）。
15．证明：恰有两个奇数度顶点u,v的无向图G是连通的,当且仅当在G上添加边（u，v）后所得的图G*是连通的。
证 必要性是显然的。
设G*是恰有两个奇数度顶点u,v的无向图G添加边（u，v）后所得，且是连通的,那么图G*是一个欧拉图（每一个顶点都是偶数度的连通图），因此G*中删除边（u，v）后所得的图G仍是连通的。
判别图8.31中各图是否为哈密顿图，若不是，请说明理由，并回答它是否有哈密顿通路。
解（a），(b) 是为哈密顿图。(c) 不是哈密顿图，也没有哈密顿通路。在图(c)中增加顶点k ，并对其顶点做二着色，构成图(d)（如下）。图(d) 不是哈密顿图，也没有哈密顿通路。因为图中白色顶点比黑色顶点多两个。故(c) 不是哈密顿图，