梯度下降法求解线性回归
梯度下降法求解线性回归
通过梯度下降法求解简单的一元线性回归
分别通过梯度下降算法和sklearn的线性回归模型(即基于最小二乘法)解决简单的一元线性回归实际案例,通过结果对比两个算法的优缺。
通过最小二乘法解决一元线性回归可以参考下面文章
https://blog.csdn.net/coffeetogether/article/details/118114217
数据源:
链接: https://pan.baidu.com/s/1KVw_9O5o9vqQnpgRNfLGVQ
提取码:8u8e
一、梯度下降算法介绍
二、梯度下降法求解线性回归
三、梯度下降法求解一元线性回归案例
1.导入数据
# 导入必要库
import numpy as np
import matplotlib.pyplot as plt
points = np.genfromtxt('E:/PythonData/machine_learning/data.csv',delimiter=',')
# 查看前5行数据
points[:5]
2.绘制散点图
# 分别提取points中的x和y数据
x = points[:,0]
y = points[:,1]
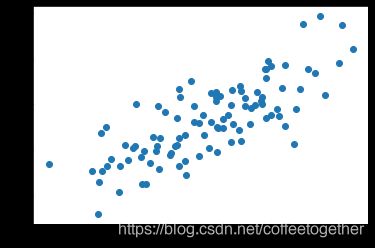
# 绘制散点图
plt.scatter(x,y)
plt.show()
3.定义损失函数
# 损失函数是系数w,b的函数,另外还要传入数据x,y
def computer_cost(w,b,points):
total_cost = 0
M = len(points)
# 逐点计算平方损失误差,然后求平均数
for i in range(M):
x = points[i,0]
y = points[i,1]
total_cost +=(y - w *x - b)**2
# 取平均
return total_cost/M
4.定义模型的超参数
# 步长
alpha = 0.0001
# 初始w
initial_w = 0
# 初始b
initial_b = 0
# 迭代次数
num_iter = 10
5.定义核心函数
def grad_desc(points,initial_w,initial_b,alpha,num_iter):
w = initial_w
b = initial_b
# 定义一个list保存所有的损失函数值,用来显示下降的过程
cost_list = []
for i in range(num_iter):
cost_list.append(computer_cost(w,b,points))
w,b = step_grad_desc(w,b,alpha,points)
return [w,b,cost_list]
def step_grad_desc(current_w,current_b,alpha,points):
sum_grad_w = 0
sum_grad_b = 0
M = len(points)
# 对每个点,代入公式求和
for i in range(M):
x = points[i,0]
y = points[i,1]
sum_grad_w += (current_w*x+current_b - y)*x
sum_grad_b += current_w*x+ current_b - y
# 用公式求当前的梯度
grad_w = 2/M*sum_grad_w
grad_b = 2/M*sum_grad_b
# 梯度下降,更新当前的w和b
updated_w = current_w - alpha*grad_w
updated_b = current_b - alpha*grad_b
return updated_w,updated_b
6.测试:运行梯度下降算法计算最优的w和b
w,b,cost_list = grad_desc(points,initial_w,initial_b,alpha,num_iter)
cost = computer_cost(w,b,points)
print('w is :',w)
print('b is :',b)
print('cost is :',cost)
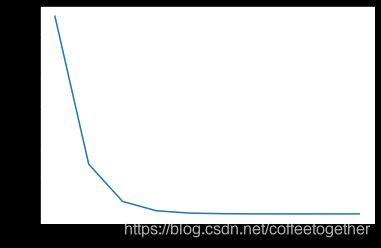
plt.plot(cost_list)
plt.show()
7.绘制拟合曲线
plt.scatter(x,y)
# 针对每一个x ,计算出预测的y值
pred_y = w*x+b
plt.plot(x,pred_y,c='r')
plt.show()
8.预测得分
pred_y1 = w*80+b
print(pred_y1)
四、通过sklearn库中的LinearRegression模型求解一元线性回归
1.导入数据
# 导入必要库
import numpy as np
import matplotlib.pyplot as plt
points = np.genfromtxt('E:/PythonData/machine_learning/data.csv',delimiter=',')
# 查看前5行数据
points[:5]
2.绘制散点图
# 分别提取points中的x和y数据
x = points[:,0]
y = points[:,1]
# 绘制散点图
plt.scatter(x,y)
plt.show()
# 损失函数是系数w,b的函数,另外还要传入数据x,y
def computer_cost(w,b,points):
total_cost = 0
M = len(points)
# 逐点计算平方损失误差,然后求平均数
for i in range(M):
x = points[i,0]
y = points[i,1]
total_cost +=(y - w *x - b)**2
# 取平均
return total_cost/M
3.通过sklearn库,求解线性回归
# 导入库
from sklearn.linear_model import LinearRegression
4.创建线性回归模型
# 创建线性回归模型
lr = LinearRegression()
# 传入数据,进行拟合
# 将数据x和y都转换成二维数据
x_new = x.reshape(-1,1)
y_new = y.reshape(-1,1)
lr.fit(x_new,y_new)
# 查看拟合结果
# 得到w参数(斜率)
w = lr.coef_[0,0]
# 得到参数b(截距)
b = lr.intercept_[0]
print('w is :',w)
print('b is :',b)
# 得出损失值
cost = computer_cost(w,b,points)
print('cost is :',cost)
5.绘制拟合曲线
plt.scatter(x,y)
# 针对每一个x,给出预测的y值
pred_y = w*x + b
plt.plot(x,pred_y,c='r')
plt.show()
6.预测得分
# 给出x值,预测得分y
x1 = 80
pred_y1 = w*x1+b
pred_y1
![]()
总结:sklearn中的LinearRegression模型的底层原理是通过最小二乘法实现的,因此对比两种方法:

通过两个方法得出的cost分别约为112,110。结果可知:在解决一元线性回归问题上,最小二乘法的效果会更佳。
由上图对比可知,最小二乘法直接通过求导找到损失函数的全局最小值,而梯度下降则是通过不断地迭代无限接近最小值。因此,在精度上最小二乘法略高于梯度下降法。