机器学习实战—支持向量机

一.简介

1.1 定义

支持向量机（SVM）是一个功能强大并且全面的机器学习模型，它能够执行线性或非线性分类、回归，甚至是异常值检测任务。它是机器学习领域最受欢迎的模型之一，SVM特别适合于中小型复杂数据集的分类

二. 线性SVM分类

2.1 简介

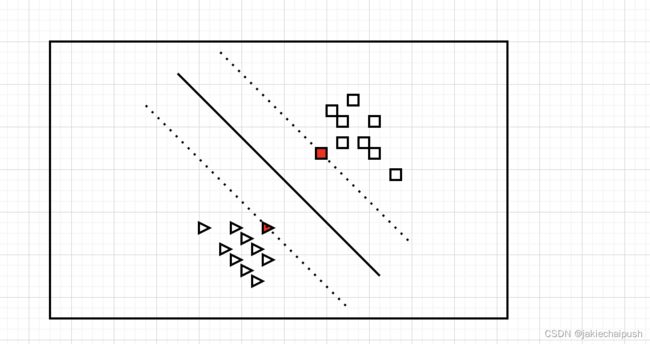
如下图是一个分类问题，图中有两个类别（三角形和正方形），这两个类别可以轻松的被一条直线分隔（说明这两个类别是线性可分离的），该图中的实线就表示的是SVM分类器的决策边界，我们可以将SVM理解为在类别之间拟合可能的最宽的街道（平行虚线所示），所以SVM也叫做大间隔分类。在街道以外的地方增加训练实例不会对决策边界产生影响，决策边界完全由街道的虚线边界所决定也可以说为支持（实线永远在两条虚线的中间），图中标红的实例就是所谓的支持向量。

注意：SVM对特征的缩放特别的敏感

2.2 软间隔分类

• 硬间隔分类

在前面提到的街道中，如果我们要求任何实例都不能出现在街道上面，且街道两边是完全不同的类别，这就是所谓的硬间隔分类，但硬间隔对于异常数据是非常敏感的，由于实现生活中数据可能会存在噪音导致街道这边的数据出现在了街道的另一边这时候我们说数据是线性不可分的，此时我们就需要使用软间隔分类来解决这类问题（软SVM）

• 软间隔分类

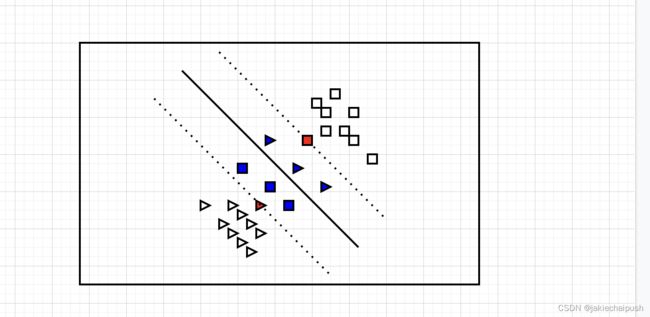
如下图蓝色点就是我们数据中出现的异常点，它运行部分样本点出现在街道上面（异常点和正常点都可以，下图只列出了异常点），在SVM思想中街道上面的点我们可以看成是无效点（不会对训练模型产生作用的点），这样我们就是排除异常然后得到较好的分类效果，这就是软分类的思想。

2.3 初步使用Sk-learn接口

下面使用鸢尾花的案例来了解SVM是如何进行分类的

import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
iris=datasets.load_iris()   #导入鸢尾花数据
X=iris['data'][:,(2,3)] #获得数据的所有行和第2列和3列数据
y=(iris['target']==2).astype(np.float64)
svm_clf=Pipeline((   #使用管道来实现
    ('scaler',StandardScaler()),
    ('linear_svc',LinearSVC(C=1,loss="hinge"))  #c表示街道宽度，loss选择svm的损失函数
))
svm_clf.fit(X,y)
svm_clf.predict([[5.5,1.7]])

结果：

三. 非线性SVM分类

3.1 简介

在现实中功能很多数据集是不能线性可分离的，处理非线性数据集的方法之一就是添加更多特征，比如特征多项式

3.2 scikit-learn实现

可以使用PolynomialFeatures来实现添加多项式

from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
polynomial_svm_clf=Pipeline((
    ("poly_features",PolynomialFeatures(degree=3)),
    ("scaler",StandardScaler()),
    ("svm_clf",LinearSVC(C=10,loss="hinge"))
))
polynomial_svm_clf.fit(X,y)

运行结果：

3.3 多项式核（解决非线性问题技术一）

前面介绍的处理非线性不可分离的数据集我们常常使用添加多项式来解决问题，但使用多项式时我们常常面临着如何确定合适的多项式的阶数，如果多项式阶数过低，处理不了复杂的数据集，如果阶数过高可能会处理过拟合问题。而svm提供了一个多项式核的技巧，它的思路是添加伪多项式（但是并没有真正添加），这样就有了多项式的效果，这个技巧由方法SVC实现，如下：

from sklearn.svm import SVC
poly_kernel_svm_cfg=Pipeline((
 ("scaler" ,StandardScaler()),
 ("svm_cfg",SVC(kernel="poly",degree=3,coef0=1,C=5))
))
poly_kernel_svm_cfg.fit(X,y)

这个使用的是3阶多项式（degree=3），coef0是一个超参数（意味着它可以通过网格搜索来处理），表示的是模型受高阶多项式还是低阶多项式影响的程度

3.4 添加相似特征（解决非线性问题技术二）

解决非线性问题的另一种技术是添加相似特征，这些特征是由相似函数计算出来的，相似函数可以测量每个实例与一个特点的坐标之间的相似度。（原来的实例会在相似函数的处理下变为新的特征），高斯函数就是我们要介绍的相似函数：

• 高斯函数RBF
  $$\varphi \gamma (X,{\rm Y})=exp(-\gamma ||X-{\rm Y}|{|}^2)$$

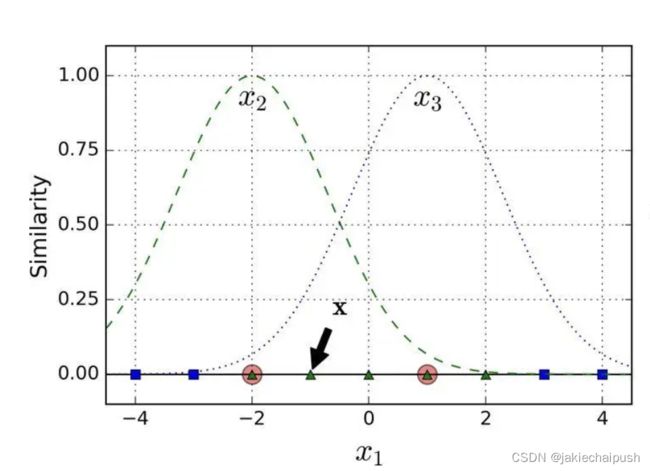
$||X-{\rm Y}||$表示的是距离，也就是实例与坐标之间的距离，高斯RBF函数图像如下：

前面介绍的核技巧同样可以用到这里，相似特征法是可以用到任意的机器学习算法的，但是要计算出所有的附加特征，其计算代价是很昂贵的，而使用核技巧它产生的结果就像添加了许多相似特征一样，但实际上没有添加。下面是高斯函数使用核的示例：

rbf_kernel_svm_clf=Pipeline((
    ("scaler",StandardScaler()),
    ("svm_clf",SVC(kernel="rbf",gamma=5,C=0.001))
))
rbf_kernel_svm_clf.fit(X,y)

gamma是一个超参数，gamma越大高斯函数图像就会越窄，反之则越宽。当然核函数的种类远远不止目前提到的两种，如何选择核函数，原则是永远先从线性函数开始尝试，特别是训练集非常大或者特征非常多的时候。

四. SVM回归

4.1 简介

前面介绍了SVM应用于线性和非线性分类问题，现在介绍的是如何用SVM去解决回归问题。与分类尝试拟合两个类别之间可能的最宽的街道的同时限制间隔违例（也就是在街道上面的实例），SVM回归要做的是尽可能多的实例位于街道上，同时限制间隔违例（也就是不在街道上的实例）。Scikit-Learn可以使用LinearSVR类来执行线性SVM回归，使用如下：

from sklearn.svm import LinearSVR
svm_reg=LinearSVR(epsilon=1.5)
svm_reg.fit(X,y)

上面解决的是线性回归问题，要解决非线性回归任务，可以用核化的SVM模型

五. SVM工作原理

5.1 决策函数和预测

线性SVM分类器通过简单地计算决策函数$w^t+b=w_1{x}_1+...+w_n{x}_n+b$来预测新实例的分类，如果结果为正类别$\hat{y}$是正类（1），否则就是负类（-1），线性svm分类器的预测函数如下：

$$\hat{y}=\{\begin{array}{l}-1if{w}^T\cdot x+b<0\\ 1if{w}^T\cdot x+b\ge 0\end{array}$$

5.2 硬间隔线性SVM分类器目标

硬间隔分类器的目标是最小化$\frac{1}{2}{w}^{T}w$，使$y_i(w^T\cdot x_i+b\ge 1(i=1,2,...,n)$这实际是一个优化问题（工程设计中最优化问题（optimization problem）的一般提法是要选择一组参数，在满足一系列有关的约束下，使设计目标达到最优值）

• 下面对硬间隔svm分类器目标的由来做一个推导

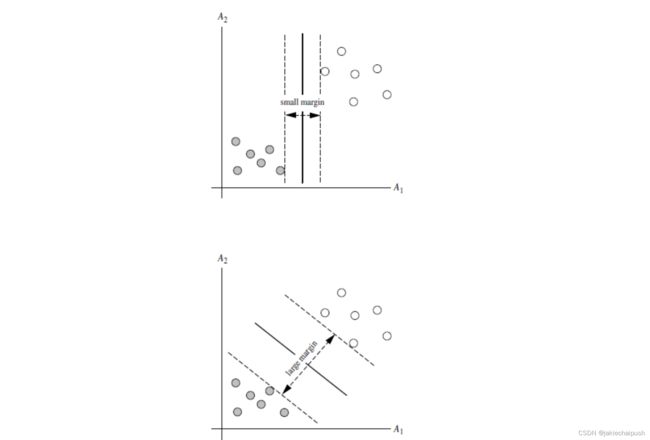
首先我们需要理解什么叫做间隔，间隔通俗的理解就是我们前面介绍到的街道的宽度，间隔的变化是和权重向量w相关的，权重向量w越小，间隔就越大，反之越小。如下图就是在不同权重向量下间隔的大小（也可以理解为不同斜率下的间隔，决策函数的斜率等于权重向量的范数，即||w||）,所以我们要最小化||w||来得到尽可能大的间隔。

前面介绍到的预测函数我们可以稍微进行一下转换，因为$\hat{y}$与$w^T\cdot x_i+b$的符号是时刻保持相同的，转换结果如下：

$$\hat{y}(w^T\cdot x+b)>0$$

我们需要求最小的样本距离，这样我们就可以联立方程组来表示约束条件下的间隔。在下面公式中我们令magin函数是用来求模型距离的函数，我们要求的是模型的最大间隔。

$$\{\begin{array}{l}d=maxmargin(w,b)\\ y_i(w^T\cdot x_i+b)>0\end{array}$$

很显然margin函数我们可以用点到直线之间的距离公式来替换来表示间隔，距离公式为$\frac{1}{||w||}|w^T\cdot x_i+b|$，所以用距离公式替换margin得到新的方程组

$$\{\begin{array}{l}d=max\frac{1}{||w||}min|w^T\cdot x_i+b|\\ y_i(w^T\cdot x_i+b)>0\end{array}$$

接着分析，我们知道$y_i(w^T\cdot x_i+b)>0$，这个不等式可以等价于必存在$\gamma >0$使得$y_i(w^T\cdot x_i+b)=\gamma$，而且我们不妨令$\gamma =1$，方程组变化为了

$$\{\begin{array}{l}d=max\frac{1}{||w||}\\ y_i(w^T\cdot x_i+b)>1\end{array}$$

求$max\frac{1}{||w||}$即求$min||w||$，即求$\frac{1}{2}{w}^{T}w$（求导即可得到||w||），这里我们就推理出了为什么硬svm的训练目标是最小化$\frac{1}{2}{w}^{T}w$，使$y_i(w^T\cdot x_i+b\ge 1(i=1,2,...,n)$

$$\{\begin{array}{l}min\frac{1}{2}{w}^{T}w\\ y_i(w^T\cdot x_i+b)>1\end{array}$$

5.3 软间隔线性SVM分类器目标

前面介绍软间隔的时候说到软间隔与硬间隔的区别就是软间隔的实例样本可以出现在街道上（即允许误差的存在），所以这里我们在硬间隔的目标上引入一个松弛变量${\rm Y}$，${\rm Y}(i)$表示的是第i个实例多大程度上运行间隔违例（出现在街道上），所以软间隔目标需要解决使松弛变量越小越好从而减少间隔违例，同时还要使$\frac{1}{2}{w}^{T}w$最小化增大间隔，这就需要权衡。那么我们该如何定义这个松弛变量呢，这里的思想是使用距离来定义，即

$$\{\begin{array}{l}{y}_i(w^T\cdot x_i+b)\ge 1,{\rm Y}=0\\ y_i(w^T\cdot x_i+b)<1,{\rm Y}=1-y_i(w^T\cdot x_i+b)\end{array}$$
等价于
$${\rm Y}(i)=max\{0,1-y_i(w^T\cdot x_i+b)\}$$

如果我们如一个${\xi }_i\ge 0$所以上面的${\rm Y}(i)$就可以直接等于${\xi }_i$，所以最后的目标变为了（c是权衡前面介绍的两个目标的超参数）：

$$\{\begin{array}{l}min\frac{1}{2}{w}^{T}w+C{\sum }_{i=1}^m{\xi }_i\\ y_i(w^T\cdot x_i+b)>1\end{array}$$