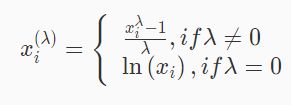sklearn中的数据预处理方法学习汇总

sklearn中的数据预处理方法学习

我们一般开始拿到的数据并非是方便我们后期分析的类型，因此需要我们进行数据的预处理。sklearn.preprocessing包提供了几个常用的函数和转换类，用它们将一个原始的特征向量转化为一个更适于数据分析的表示形式。一般来说，学习算法收益于数据集的标准形式。如果数据中存在异常点，稳健的数据规范或转换是更适合的。
这里整理了一些常用的数据预处理方法，不过更多的是在介绍如何使用，而没有具体说在哪里使用，因此需要自己判断使用的情况，后面如果有机会，会把每个方法的详细介绍补上去。

一、标准化

对于大多数数据挖掘算法来说，数据集的标准化是基本要求。如果特征不服从或者近似服从标准正态分布（即，零均值、单位标准差的正态分布）的话，算法的表现会大打折扣。例如，我们经常忽略数据的分布形状，而仅仅做零均值、单位标准差的处理。在一个机器学习算法的目标函数里的很多元素所有特征都近似零均值，方差具有相同的阶。如果某个特征的方差的数量级大于其它的特征，那么，这个特征可能在目标函数中占主导地位，这使得模型不能从其它特征有效地学习。

Z-score标准化

Z-score标准化学习

想系统了解点这里：Z-score是什么.下面是简要的介绍：

Z-Score标准化是数据处理的一种常用方法。通过它能够将不同量级的数据转化为统一量度的Z-Score分值进行比较。数据分析与挖掘中，很多方法需要样本符合一定的标准，如果需要分析的诸多自变量不是同一个量级，就会给分析工作造成困难，甚至影响后期建模的精准度。

举例来说，假设我们要比较A与B的考试成绩，A的考卷满分是100分（及格60分），B的考卷满分是700分（及格420分）。很显然，A考出的70分与B考出的70分代表着完全不同的意义。但是从数值来讲，A与B在数据表中都是用数字70代表各自的成绩。

那么如何能够用一个同等的标准来比较A与B的成绩呢？Z-Score就可以解决这一问题。

这种方法基于原始数据的均值mean和标准差standard deviation进行数据的标准化。将特征A的原始值x使用z-score标准化到x’。z-score标准化方法适用于特征A的最大值和最小值未知的情况，或有超出取值范围的离群数据的情况。将数据按其特征(按列进行)减去其均值，然后除以其方差。最后得到的结果是，对每个特征/每列来说所有数据都聚集在0附近，方差值为1。数学公式如下：

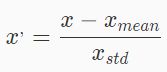
（x：观测值；x mean:总体平均值；x std:总体标准差）

Z-score标准化实现

函数scale为数组形状的数据集的标准化提供了一个快捷实现：

from sklearn import preprocessing  
import numpy as np  
X_train = np.array([[ 1., -1.,  2.],  
                    [ 2.,  0.,  0.],  
                    [ 0.,  1., -1.]])  
X_scaled = preprocessing.scale(X_train)
print(X_scaled)

'''[[ 0.         -1.22474487  1.33630621]
 [ 1.22474487  0.         -0.26726124]
 [-1.22474487  1.22474487 -1.06904497]]'''

经过缩放后的数据具有零均值以及标准方差:

print(X_scaled.mean(axis=0))
#[0. 0. 0.]
print(X_scaled.std(axis=0))
#[1. 1. 1.]

Min-max标准化

Min-max标准化方法是对原始数据进行线性变换。设minA和maxA分别为特征A的最小值和最大值，将A的一个原始值x通过min-max标准化映射成在区间[0,1]中的值x'，其公式为：

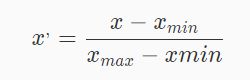
这个比较好理解，给出一个简单的图示例：

可以使用MinMaxScaler实现，以下是一个将简单的数据矩阵缩放到[0, 1]的例子:

from sklearn import preprocessing  
import numpy as np  
X_train = np.array([[ 1., -1.,  2.],  
                    [ 2.,  0.,  0.],  
                    [ 0.,  1., -1.]])
min_max_scaler = preprocessing.MinMaxScaler()
X_train_minmax = min_max_scaler.fit_transform(X_train)
print(X_train_minmax)
'''
[[0.5        0.         1.        ]
 [1.         0.5        0.33333333]
 [0.         1.         0.        ]]'''

MaxAbs标准化

MaxAbs的工作原理与Min-max非常相似，但它只通过除以每个特征的最大值将训练数据特征缩放至 [-1, 1] 范围内，这就意味着，训练数据应该是已经零中心化或者是稀疏数据。公式如下：

可以使用MaxAbsScale实现，以下是使用上例中数据运用这个缩放器的例子:

from sklearn import preprocessing  
import numpy as np  
X_train = np.array([[ 1., -1.,  2.],  
                    [ 2.,  0.,  0.],  
                    [ 0.,  1., -1.]])
max_abs_scaler = preprocessing.MaxAbsScaler()
X_train_maxabs = max_abs_scaler.fit_transform(X_train)
print(X_train_maxabs)
'''
[[ 0.5 -1.   1. ]
 [ 1.   0.   0. ]
 [ 0.   1.  -0.5]]'''

二、非线性转换

上面我们说过，对于大多数数据挖掘算法来说，如果特征不服从或者近似服从标准正态分布（即，零均值、单位标准差的正态分布）的话，算法的表现会大打折扣。非线性转换就是将我们的特征映射到均匀分布或者高斯分布(即正态分布)。

映射到均匀分布

相比线性缩放，该方法不受异常值影响，它将数据映射到了零到一的均匀分布上，将最大的数映射为1，最小的数映射为0。其它的数按从小到大的顺序均匀分布在0到1之间，如有相同的数则取平均值，如数据为np.array([[1],[2],[3],[4],[5]])则经过转换为：np.array([[0],[0.25],[0.5],[0.75],[1]])，数据为np.array([[1],[2],[9],[10],[2]])则经过转换为：np.array([[0],[0.375],[0.75],[1.0],[0.375]])。第二个例子具体过程如下图：

在sklearn中使用QuantileTransformer方法实现：

from sklearn.preprocessing import QuantileTransformer
import numpy as np
data = np.array([[1],[2],[3],[4],[5]])
quantile_transformer = QuantileTransformer(random_state=666)
data = quantile_transformer.fit_transform(data)
print(data)

'''[[0.  ]
 [0.25]
 [0.5 ]
 [0.75]
 [1.  ]]'''

映射到高斯分布

映射到高斯分布是为了稳定方差，并最小化偏差。在sklearn 0.20.x中PowerTransformer现在有两种映射方法，Yeo-Johnson映射，公式如下：

Box-Cox映射，公式如下：

在sklearn 0.20.x中使用PowerTransformer方法实现，用法如下：

from sklearn.preprocessing import PowerTransformer
import numpy as np
data = np.array([[1],[2],[3],[4],[5]])
pt = PowerTransformer(method='box-cox', standardize=False)
data = pt.fit_transform(data) 
print(data)
'''
[[0.        ]
 [0.88891532]
 [1.64391667]
 [2.32328259]
 [2.95143046]]'''

三、归一化

归一化的作用

对于范数的学习推荐去看这篇文章，点击进入.
这一部分更偏向于记录，个人觉得小白这部分单纯去看很难想象出具体有什么用，怎么去用，可以多看看实际的例子。

归一化是缩放单个样本以具有单位范数的过程。归一化实质是一种线性变换，线性变换有很多良好的性质，这些性质决定了对数据改变后不会造成“失效”，反而能提高数据的表现，这些性质是归一化的前提。归一化能够加快模型训练速度，统一特征量纲，避免数值太大。值得注意的是，归一化是对每一个样本做转换，所以是对数据的每一行进行变换。而之前的方法是对数据的每一列做变换。

L1范式归一化

L1范式定义如下：

从公式看就是向量x中每个元素的绝对值之和。
L1范式归一化就是将样本中每个特征除以特征的L1范式。

在sklearn中使用normalize方法实现，用法如下：

from sklearn.preprocessing import normalize
import numpy as np
data = np.array([[-1,0,1],
                 [1,0,1],
                 [1,2,3]])
data = normalize(data,'l1')
print(data)
'''
[[-0.5         0.          0.5       ]
 [ 0.5         0.          0.5       ]
 [ 0.16666667  0.33333333  0.5       ]]'''

L2范式归一化

L2范式定义如下：

表示向量元素的平方和再开平方根。
L2范式归一化就是将样本中每个特征除以特征的L2范式。

在sklearn中使用normalize方法实现，用法如下：

from sklearn.preprocessing import normalize
import numpy as np
data = np.array([[-1,0,1],
                 [1,0,1],
                 [1,2,3]])
data = normalize(data,'l2')
print(data)
'''
[[-0.70710678  0.          0.70710678]
 [ 0.70710678  0.          0.70710678]
 [ 0.26726124  0.53452248  0.80178373]]'''

四、离散值编码

LabelEncoder

在数据挖掘中，特征经常不是数值型的而是分类型的。举个例子，一个人可能有["male", "female"]，["from Europe", "from US", "from Asia"]，["uses Firefox", "uses Chrome", "uses Safari", "uses Internet Explorer"]等分类的特征。这些特征能够被有效地编码成整数，比如["male", "from US", "uses Internet Explorer"]可以被表示为[0, 1, 3]，["female", "from Asia", "uses Chrome"]表示为[1, 2, 1]。

在sklearn中，通过LabelEncoder来实现：

from sklearn.preprocessing import LabelEncoder
label = ['male','female']
int_label = LabelEncoder()
label = int_label.fit_transform(label)
print(label)
# [1 0]

OneHotEncoder

这种整数特征表示并不能在sklearn的估计器中直接使用，因为这样的连续输入，估计器会认为类别之间是有序的，但实际却是无序的。如将male,female，转换为1,0。1比0要大，机器就会把这个关系考虑进去，而male,female之间是没有这样的关系的。所以我们需要使用另外一种编码方式，OneHot编码。

在sklearn中通过OneHotEncoder来实现，使用方法如下：

import numpy as np
from sklearn.preprocessing import OneHotEncoder
label = np.array([1,0])
label = np.array(label).reshape(len(label),1)#先将X组织成（sample，feature）的格式
onehot_label = OneHotEncoder()
label = onehot_label.fit_transform(label).toarray()
print(label)
'''[[0. 1.]
 [1. 0.]]'''

五、生成多项式特征

多项式特征的作用

在数据挖掘中，获取数据的代价经常是非常高昂的。所以有时就需要人为的制造一些特征，并且有的特征之间是有关联的。生成多项式特征可以轻松的为我们获取更多的数据，并获得特征的更高维度和互相间关系的项且引入了特征之间的非线性关系，可以有效的增加模型的复杂度。

PolynomialFeatures

在sklearn中通过PolynomialFeatures方法来生成多项式特征，使用方法如下：

import numpy as np
from sklearn.preprocessing import PolynomialFeatures
data = np.arange(6).reshape(3, 2)
poly = PolynomialFeatures(2)#生成二项式特征
data = poly.fit_transform(data)
print(data)
'''
[[ 1.  0.  1.  0.  0.  1.]
 [ 1.  2.  3.  4.  6.  9.]
 [ 1.  4.  5. 16. 20. 25.]]'''

特征转换情况如下：

在一些情况下，只需要特征间的交互项，这可以通过设置 interaction_only=True来得到:

import numpy as np
from sklearn.preprocessing import PolynomialFeatures
data = np.arange(6).reshape(3, 2)
poly = PolynomialFeatures(degree=2, interaction_only=True)#degree=n表示生成n项式特征，只需要特征之间交互
data = poly.fit_transform(data)
print(data)
'''
[[ 1.  0.  1.  0.]
 [ 1.  2.  3.  6.]
 [ 1.  4.  5. 20.]]'''

特征转换情况如下：

六、估算缺失值

估算缺失值的作用

由于各种原因，真实世界中的许多数据集都包含缺失数据，这类数据经常被编码成空格、NaNs，或者是其他的占位符。但是这样的数据集并不能被sklearn学习算法兼容，因为大多的学习算法都默认假设数组中的元素都是数值，因而所有的元素都有自己的意义。 使用不完整的数据集的一个基本策略就是舍弃掉整行或整列包含缺失值的数据。但是这样就付出了舍弃可能有价值数据（即使是不完整的 ）的代价。 处理缺失数值的一个更好的策略就是从已有的数据推断出缺失的数值。

Imputer

sklearn中使用Imputer方法估算缺失值，使用方法如下：

from sklearn.preprocessing import Imputer
data = [[np.nan, 2], [6, np.nan], [7, 4],[np.nan,4]]  
imp = Imputer(missing_values='NaN', strategy='mean', axis=0)#缺失值为nan，沿着每一列，使用平均值来代替缺失值  
data = imp.fit_transform(data)
print(data)
'''
	   [[6.5       , 2.        ],  
       [6.        , 3.33333333],  
       [7.        , 4.        ],  
       [6.5       , 4.        ]]'''

其中strategy参数用来选择代替缺失值方法：

1.mean表示使用平均值代替缺失值

2.median表示使用中位数代替缺失值

3.most_frequent表示使用出现频率最多的值代替缺失值

missing_values参数表示何为缺失值：

1.NaN表示np.nan为缺失值

2.0表示0为缺失值