【卷积神经网络】卷积与卷积层

什么是卷积

首先我们先来回顾一下卷积公式“

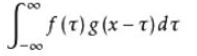
它的物理意义大概可以理解为：系统某一时刻的输出是由多个输入共同作用（叠加）的结果。

放在图像分析里，f(x) 可以理解为原始像素点(source pixel)，所有的原始像素点叠加起来，就是原始图了。

g(x)可以称为作用点，所有作用点合起来我们称为卷积核（Convolution kernel）

卷积核上所有作用点依次作用于原始像素点后（即乘起来），线性叠加的输出结果，即是最终卷积的输出，也是我们想要的结果，我们称为destination pixel.

具体原理可以见下图：

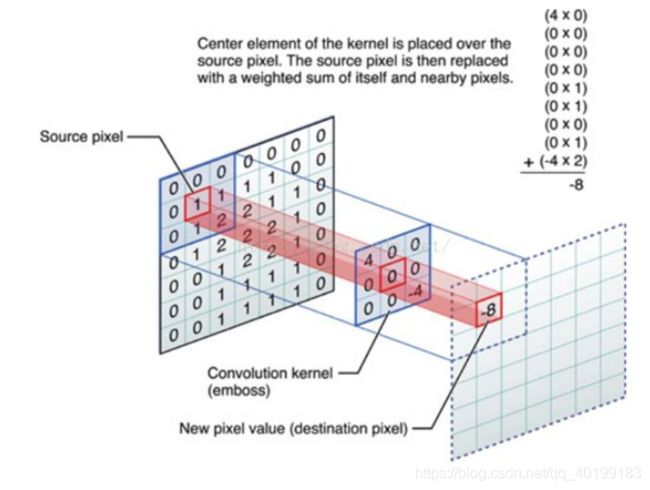
最左边呢就是我们原始输入图像了，中间呢是卷积层，-8就是卷积的结果。

卷积层在神经网络中的作用

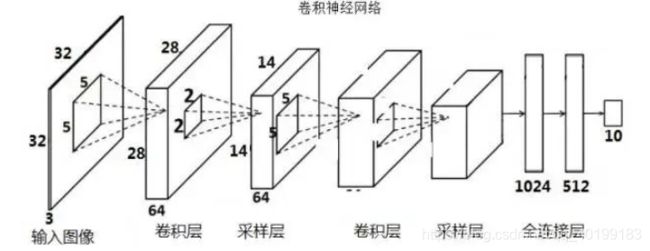
上图是一个较为常见的卷积神经网络的示意图。
卷积神经网络说到底，终究是起到一个分类器的作用，卷积层负责提取特征，采样层负责特征选择，全连接层负责分类。

下面举个例子来介绍卷积层是如何进行特征提取的

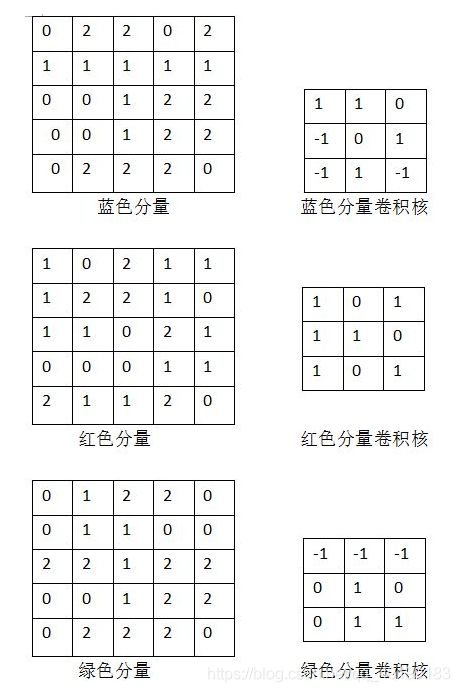
正常情况下，我们输入图片是RGB格式，也就对红®、绿(G)、蓝(B)三个颜色，这三个通道的颜色叠加之后，就是我们看到的RGB图片了

如下图

我们假设，这三个通道的像素值分别如下所示：

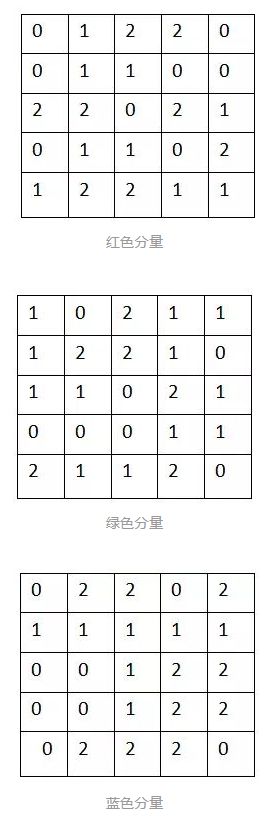
在得到这三个通道的RGB分量之后，我们就可以使用卷积核（滤波器 / convolution kernel）来提取特征

图像和卷积核进行卷积，就可以得到特征值，就是destination value

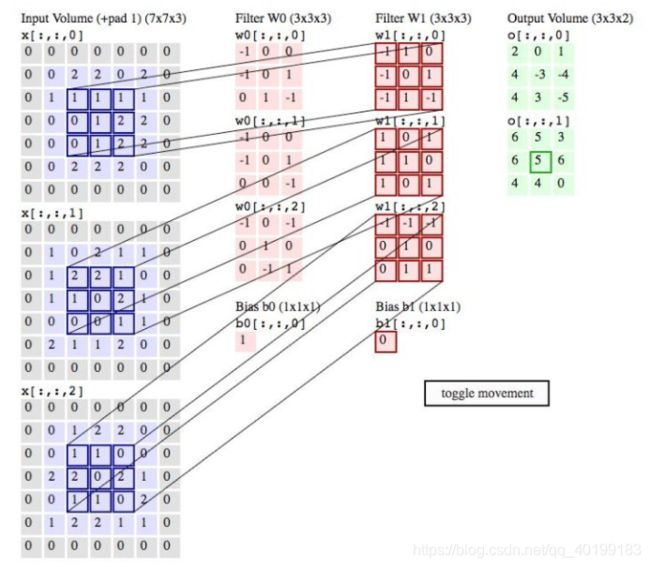
具体原理如下图所示：

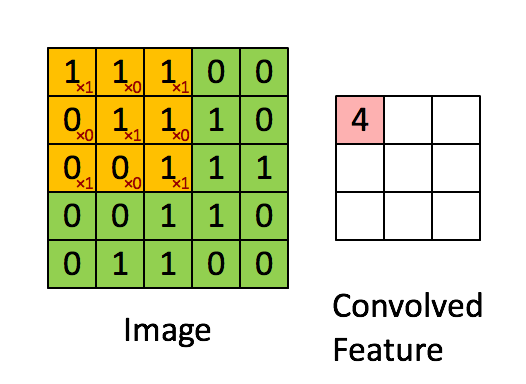
其中，卷积核在神经网络中，就代表权重（weight）

卷积核和图像进行点乘（dot product），就代表卷积核里的权重单独对相应位置的像素值进行作用

值得注意的是，这里我们虽然称其为卷积，实际上是位置一一对应的点乘，不是真正意义上的卷积

至于为什么要把点乘完所有结果加起来，实际上就是把所有作用效果叠加起来

就好比前面提到的RGB图片，红绿蓝分量叠加起来产生了一张真正意义的美女图

在卷积神经网络中，卷积核内部的权值传统上是由反向传播算法得来的，在这里不作拓展

假设我们已经知道对应分量以及卷积核

由于卷积核是3x3的

所以我们分别对三个分量的其中一个3x3的九宫格进行卷积

比如我们在分量的中间找一个3x3九宫格

所以，结果为：

W1output = 1*(-1) +11+10+0*(-1)+10+21+0*(-1)+11+2(-1) =1

W2output = 21+20+11+11+01+02+01+00+1*1=5

W3output = 1*(-1)+1*(-1)+0*(-1)+02+0(1)+02+10+11+01 = -1

Bias = 0 # 偏置我们暂且设为0

Final_output =W1output + W2output+W3output+bias= 1+5-1+0 = 5

我们将三个卷积核的输出叠加在一起可以看作是三个颜色的特征分量叠加成RGB特征分量

在此我们就完成了利用卷积层对图像提取特征

在严格意义上，我们卷积层输出的特征图（feature map），除了特征值本身外，还包含了相对位置信息

比如人脸检测，眼睛，鼻子，嘴巴都是从上到下排列的

那么提取出的相应的特征值也是按照这个顺序排列的

再举个例子

我们按顺序去看这三个方块

我们可以非常容易的看出这个是数字“2”

这样，就看不出是‘2’了

所以，我们卷积的方式也希望按照正确的顺序

因此，我们实现卷积运算最后的方式

就是从左到右，每隔x列像素（步长为x），向右移动一次卷积核进行卷积(x可以自己定义)

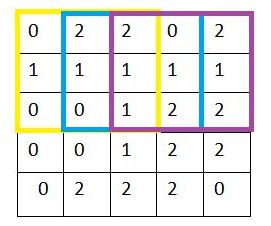
黄—蓝---紫，就是卷积核移动的顺序，这里x =1

当第一行结束遍历之后，再向下跳转到间隔y行的像素开始继续从左至右遍历，此处y也需自行设定

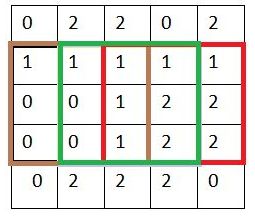
就这样，我们先从左到右，再从上到下，直到所有像素被卷积核过了一遍，完成输入图片的第一层卷积层的特征提取

这里的x我们叫作stride,就是步长的意思，如果我们x = 2, 就是相当每隔两行或者两列进行卷积

在结束遍历之后，我们会在得到的特征图最外圈补0（zero padding）

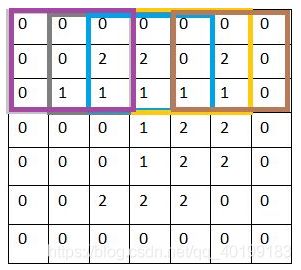
添加了一圈零，其实实际上我们什么信息也没有添加，但是同样在步长为1的情况下，补0比原来没有补0的情况下进行卷积，这样其这一层卷积层输出的特征图（feature map）仍然为55，保证了输入输出图像大小的一致。而如果没有补0，则输出图像大小就会变成33

这样做有以下好处：

（1）我们获得的更多更细致的特征信息，上面那个例子我们就可以获得更多的图像边缘信息

（2）我们可以控制卷积层输出的特征图的size，从而可以达到控制网络结构的作用，还是以上面的例子，如果没有做zero-padding以及第二层卷积层的卷积核仍然是3x3, 那么第二层卷积层输出的特征图就是1x1，CNN的特征提取就这么结束了。

同样的情况下加了zero-padding的第二层卷积层输出特征图仍然为5x5,这样我们可以再增加一层卷积层提取更深层次的特征

额外补充

同样提取某个特征**，经过不同卷积核卷积后效果也不一样（这是个重点，为什么说重点，因为CNN里面卷积核的大小就是有讲究的）**。

比如说：

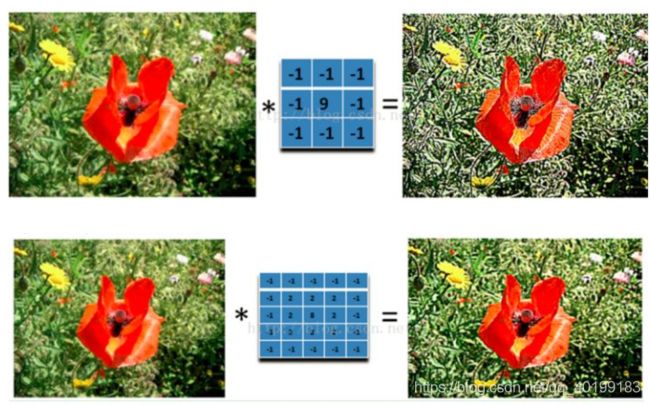
可以发现同样是锐化，下图5x5的卷积核要比上图3x3的卷积核效果细腻不少。

再补充一点卷积核的知识点：

（1）原始图像通过与卷积核的数学运算，可以提取出图像的某些指定特征（features)。

（2）不同卷积核，提取的特征也是不一样的。

（3）提取的特征一样，不同的卷积核，效果也不一样。