感知机python代码实现

目录

1、数据集准备

1.1 导入包

1.2 加载数据

1.3 原始数据可视化

 1.4划分数据集和标签

2、感知机实现

2.1 初始化w、b、以及步长

2.2 设计激活函数

2.3 随机梯度下降

2.4 实现

 3、检验

---

1、数据集准备

        本文使用sklearn的鸢尾花数据。

       sklearn.datasets.load_iris(*, return_X_y=False, as_frame=False)
       Iris数据集是常用的分类实验数据集，由Fisher, 1936收集整理。Iris也称鸢尾花卉数据集，是一类多重变量分析的数据集。数据集包含150个数据样本，分为3类，每类50个数据，每个数据包含4个属性（分别是：花萼长度，花萼宽度，花瓣长度，花瓣宽度）。可通过这4个属性预测鸢尾花卉属于（Setosa，Versicolour，Virginica）三个种类的鸢尾花中的哪一类。
Iris里有两个属性iris.data，iris.target。data是一个矩阵，每一列代表了萼片或花瓣的长宽，一共4列，每一列代表某个被测量的鸢尾植物，一共有150条记录。

1.1 导入包

import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

1.2 加载数据

iris = load_iris()用来加载数据
df['label'] = iris.target划分数据的标签
这里我们只取花萼长度，花萼宽度，花瓣长度，花瓣宽度为属性
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']

iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
df.label.value_counts()

1.3 原始数据可视化

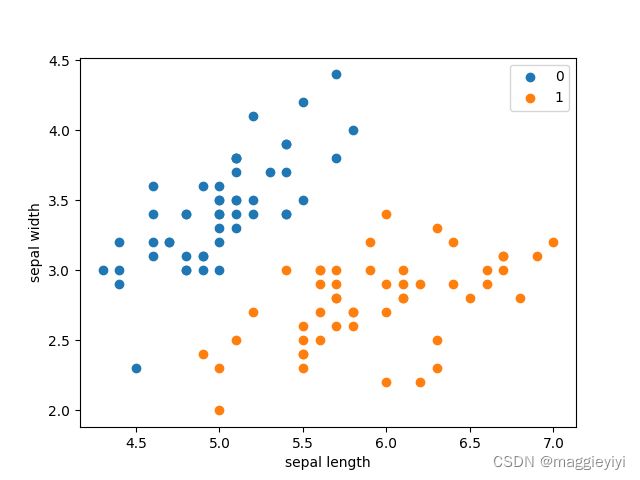
按照花萼长度，花萼宽度进行可视化数据划分，0-49为0类，50-99为1类。

plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')

 1.4划分数据集和标签

        由于感知机是二分类的划分，因此本次选取鸢尾花的前两个类型进行训练预测。也就是前100个数据（0-99）。并且输入维度控制为2维，所以选取第0、1列特征。最后一列是target。并且按照感知机原理将y值设为-1、1的二分类。

data = np.array(df.iloc[:100, [0, 1,-1]])
X, y = data[:, :-1], data[:, -1]
y = np.array([1 if i == 1 else -1 for i in y])

2、感知机实现

2.1 初始化w、b、以及步长

    def __init__(self):
        self.w = np.ones(len(data[0]) - 1, dtype=np.float32)
        self.b = 0
        self.l_rate = 0.1

2.2 设计激活函数

    def sign(self, x, w, b):
        y = np.dot(x, w) + b
        return y

2.3 随机梯度下降

    def fit(self, X_train, y_train):
        is_wrong = False
        while not is_wrong:
            wrong_count = 0
            for d in range(len(X_train)):
                X = X_train[d]
                y = y_train[d]
                if y * self.sign(X, self.w, self.b) <= 0:
                    self.w = self.w + self.l_rate * np.dot(y, X)
                    self.b = self.b + self.l_rate * y
                    wrong_count += 1
            if wrong_count == 0:
                is_wrong = True
        return 'Perceptron Model!'

2.4 实现

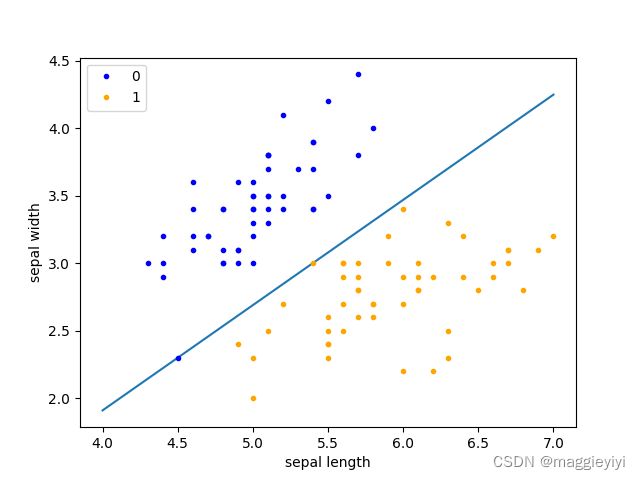
将上述类实现，并可视化展示

二分类线性函数用

x_points = np.linspace(4, 7, 10) y_ = -(perceptron.w[0] * x_points + perceptron.b) / perceptron.w[1] plt.plot(x_points, y_)
其中：y_ = -(perceptron.w[0] * x_points + perceptron.b) / perceptron.w[1]

可以理解为已知法向量和x以及截距b求y的值。

perceptron = Model()
perceptron.fit(X, y)
x_points = np.linspace(4, 7, 10)
y_ = -(perceptron.w[0] * x_points + perceptron.b) / perceptron.w[1]
plt.plot(x_points, y_)
#
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
plt.show()

 3、检验

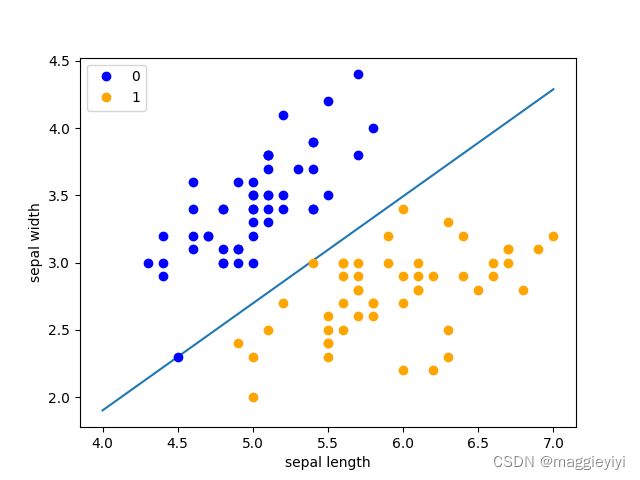
利用sklearn自带的感知机函数进行检验

from sklearn.linear_model import Perceptron

# In[13]:


clf =  Perceptron(fit_intercept=True, max_iter=1000, shuffle=True, eta0=0.1, tol=None)
clf.fit(X, y)

# In[14]:


# Weights assigned to the features.
print(clf.coef_)

# In[15]:


# 截距 Constants in decision function.
print(clf.intercept_)

# In[16]:


x_ponits = np.arange(4, 8)
y_ = -(clf.coef_[0][0] * x_ponits + clf.intercept_) / clf.coef_[0][1]
plt.plot(x_ponits, y_)

plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
plt.show()