机器学习——感知机(笔记+代码)
机器学习——感知机
感知机模型定义:
1、输入空间![]() ,目的是根据数据求出一个f(x),使得输入空间映射的输出空间;
,目的是根据数据求出一个f(x),使得输入空间映射的输出空间;
![]()
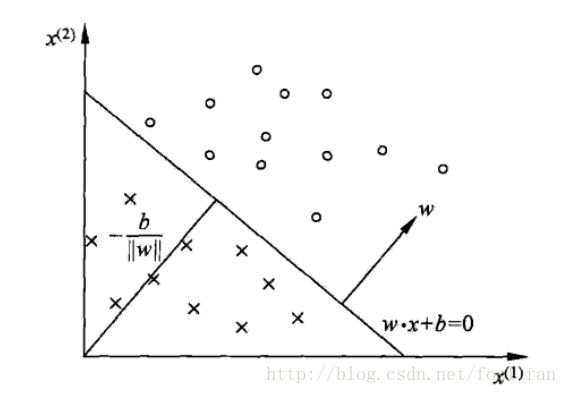
当![]() = 0时是一个超平面,该平面讲空间中的数据分成两类,这就是感知机的二分模型。我们的目的是找到一个当使得具有最好(在训练集上最好,)的分类效果。其中,
= 0时是一个超平面,该平面讲空间中的数据分成两类,这就是感知机的二分模型。我们的目的是找到一个当使得具有最好(在训练集上最好,)的分类效果。其中,![]() 叫做权重向量(或者是法向量),
叫做权重向量(或者是法向量),![]() 叫做偏移值(或者是截距)。
叫做偏移值(或者是截距)。
图例:
参数的学习策略:
数据集:![]() ,要求数据集线性可分。
,要求数据集线性可分。
目标:

我们的任何优化问题,都是基于损失函数最小化进行求解的,因此现在需要找到损失函数;
1、错误分类的点的个数,(不是w,b的连续可导函数,不易于优化,这个概念很重要)
2、错误分类的点到超平面的距离,(与上面相对,可以进行求导优化(梯度))
例如x0到超平面s的距离:
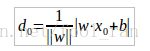
从上面目标可知,错误分类的点满足:![]() ,因此误分类的点到超平面s的距离是:
,因此误分类的点到超平面s的距离是:![]() ,==> 总的误分类距离的和是
,==> 总的误分类距离的和是![]() 。M:是误分类的集合。
。M:是误分类的集合。
运算的时候,可以忽略确定的系数,因此![]() 的损失函数可以定义为:
的损失函数可以定义为:
![]()
目标是最小化损失函数,求导得到极小值(专业点叫做随机梯度下降);
![]()
求解:

注意:算法有可能会陷入局部最优。
Code:
# coding: utf-8
# In[4]:
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
# In[71]:
class Perceptron:
trainSet = np.nan
labels = np.nan
w = 0
b = 0
def __init__(self):
pass
def plot(self):
'''
显示每一次的直线的位置
'''
for i in range(self.trainSet.shape[0]):
if self.labels[i] == 1:
plt.scatter(self.trainSet[i][0],self.trainSet[i][1],marker = 'o', s=200, c='red')
else:
plt.scatter(self.trainSet[i][0],self.trainSet[i][1],marker = 'x', s=200, c='black')
x = np.arange(0, 5)
y = -(x * self.w[0] + self.b) / self.w[1]
plt.plot(x,y,c = 'blue')
plt.show() # 显示训练的过程
def plotAll(self):
w = np.zeros(self.trainSet.shape[1])
b = 0
learnRate = 1
flag = True
length = self.trainSet.shape[0]
i = 0
while flag:
flag = False
for i in range(length):
t = self.labels[i] * (np.sum(self.trainSet[i] * w) + b)
# print(t)
if t <= 0: #错误分类的点,修改权重
w = w + learnRate * self.labels[i] * self.trainSet[i]
b = b + learnRate * self.labels[i]
flag = True
print(w,b)
i += 1
# 修改类的值
self.w = w
self.b = b
# plot
for i in range(self.trainSet.shape[0]):
if self.labels[i] == 1:
plt.scatter(self.trainSet[i][0],self.trainSet[i][1],marker = 'o', s=200, c='red')
else:
plt.scatter(self.trainSet[i][0],self.trainSet[i][1],marker = 'x', s=200, c='black')
x = np.arange(0, 5)
y = -(x * self.w[0] + self.b) / self.w[1]
plt.plot(x,y,c = 'blue')
plt.show()
def loadDataSet(self,trainData,labels):
'''
格式化训练数据
'''
return np.array(trainData), np.array(labels)
def fit(self,trainData,label,learnRate=1):
'''
原始训练数据和labels,以及学习率(0 < learnRate <= 1)
'''
self.trainSet = np.array(trainData)
self.labels = np.array(label)
w = np.zeros(self.trainSet.shape[1])
b = 0
flag = True
length = self.trainSet.shape[0]
while flag:
flag = False
for i in range(length):
t = self.labels[i] * (np.sum(self.trainSet[i] * w) + b)
# print(t)
if t <= 0: #错误分类的点,修改权重
w = w + learnRate * self.labels[i] * self.trainSet[i]
b = b + learnRate * self.labels[i]
flag = True
# print(w,b)
# 修改类的值
self.w = w
self.b = b
# self.plot()
return w, b
def predict(self,testSet):
'''
测试数据
'''
data = []
if type(testSet[0]) is not list:
data.append(testSet)
testSet = np.array(data)
else:
testSet = np.array(testSet)
# print(testSet, testSet.shape[0])
result = []
for i in range(testSet.shape[0]):
a = np.sign(np.sum(self.w * testSet[i]) + self.b)
# print(a,np.sum(self.w * testSet[i]) + self.b)
result.append(a)
return result
# In[72]:
perceptron = Perceptron()
# [[1,1],[1,2],[2,1],[4,4],[4,5],[5,6]],[+1, +1, +1, -1, -1, -1]
# In[73]:
perceptron.fit([[1,1],[1,2],[2,1],[4,4],[4,5],[5,6]],[+1, +1, +1, -1, -1, -1])
# In[74]:
# perceptron.plotAll()
# In[76]:
perceptron.predict([[2,2],[1,2],[4,3]])