《机器学习实战》5.Logistic回归

目录

1 基于logistic回归和sigmoid函数的分类

2 基于最优化方法的最佳回归系数确定

2.1 梯度上升法

 2.2 训练算法：使用梯度上升找到最佳参数

2.3 分析数据：画出决策边界

 2.4 训练算法：随机梯度上升

 3 示例：从疝气病症预测病马的死亡率

3.1 准备数据：处理数据中的缺失值

3.2 测试算法：用logistic回归进行分类

 4 本章小结

---

本章设计到的相关代码和数据

本章内容

①sigmoid函数和logistic回归分类器  

②最优化理论初步  

③梯度下降最优化算法  

④数据中的缺失项处理  

假设我们现在有一些数据点，我们用一条直线对这些点进行拟合（该线称为最佳拟合直线），这个拟合的过程就叫做回归  

 logistic回归进行分类的主要思想就是：根据现有数据对分类边界线建立回归公式，一次进行分类，“回归”一词源于最佳拟合，标识要找到最佳拟合参数集。

一般过程 

①收集数据：采用任意方法收集  

②准备数据：由于需要进行距离计算，因此要求数据类型为数值型。另外，结构化数据格式则最佳 

③分析数据：采用任意方法对数据进行分析  

④训练算法：大部分时间将用于训练，训练的目的是为了找到最佳的分类回归系数  

⑤测试算法：一旦训练完成，分类将会很快  

⑥使用算法：首先，我们需要输入一些数据，并将其转换成对应的结构化数值，接着，基于训练好的回归系数就可以对这些数值进行简单的回归计算，判定他们属于哪个类别；在这之后，我们就可以在输出的类别上做一些其他的分析工作

1 基于logistic回归和sigmoid函数的分类

Logistic回归

优点：计算代价不高，易于理解和实现

缺点：容易欠拟合，分类精度可能不高

适用数据类型：数值型和标称型数据

我们想要的函数应该是，能接受所有的输入然后预测出类别。例如，在两个类的情况下，函数输出0或1。这种函数称为单位阶跃函数。其中一个函数就具有这样类似的性质，且在数学上更易处理，这就是sigmoid函数。但是如何确定最佳的回归系数和回归系数的大小，就是一个问题

2 基于最优化方法的最佳回归系数确定

sigmoid函数的输入记为z，由下面公式可以得出，z=w0x0+w1x1+w1x1+...+wnxn  

其中的向量z是分类器的输入数据，向量w也就是我们要找到的最佳参数  

关于如何找到最佳参数，我们首先认识梯度上升的最优化方法

2.1 梯度上升法

基本思想：要找到某个函数的最大值，最好的方法就是沿着该函数的梯度方向寻找，直至找到某个临界值，或者是达到某个可以允许的误差范围

 2.2 训练算法：使用梯度上升找到最佳参数

我们一共有100个样本点，每个样本点包含两个数值型特征：x1和x2.在此数据集上，我们将通过使用梯度上升法找到最佳回归系数，也就是拟合出logistic回归模型的最佳参数。

 梯度上升法的伪代码如下：

每个回归系数初始化为1

重复n次：  

    计算整个数据集的梯度  

    使用alpha*gradient更新回归系数的向量  

    返回回归系数  

 代码如下：

import numpy as np
# 加载数据函数
def loadDataSet():
    dataMat=[]
    labelMat=[]
    # 打开文本文件
    fr=open('testSet.txt')
    # 按行读取文件
    for line in fr.readlines():
        # strip()默认删除字符串中的空格，换行等，如果是strip（s）就是删除字符串中的s
        # split()函数用于分割字符串
        lineArr=line.strip().split()
        # 将xy坐标对放到数据组里
        dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])
        # 放到标签组里
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat

# sigmoid函数   inX是一个向量
def sigmoid(inX):
    return 1/(1+np.exp(-inX))

# 梯度上升法
def gradAscent(dataMatIn,classLabels):
    # np.mat矩阵将输入解释为矩阵，np.matrix函数用于从类数组对象或数据字符串返回矩阵，np.array（）函数用于创建一个数组
    dataMatrix=np.mat(dataMatIn)
    # transpose函数求转置矩阵
    labelMat=np.mat(classLabels).transpose()
    # 获得矩阵的维数
    m,n=np.shape(dataMatrix)
    # 目标移动的步长
    alpha=0.001
    # 迭代次数
    maxCycles=500
    # 得到一个n行1列全是1 的矩阵
    weights=np.ones((n,1))
    print(weights)
    # 循环进行迭代   矩阵相乘
    for k in range(maxCycles):
        # 计算sigmoid函数的值    h是一个列向量
        h=sigmoid(dataMatrix*weights)
        # 得到误差值，在这里计算真实类别和预测类别之间的差值，就是按照该差值的方向调整回归系数
        error=(labelMat-h)
        # weight是最优参数
        weights=weights+alpha*dataMatrix.transpose()*error
    return weights

调用上面代码：

dataArr,labelMat=loadDataSet()
print(dataArr)
# 得到最优的权重信息
weight=gradAscent(dataArr,labelMat)
weight

得到的输出结果如下：

2.3 分析数据：画出决策边界

代码如下：

# 画出数据集和logistic回归最佳拟合直线的函数
import numpy as np
def plotBestFit(weights):
    import matplotlib.pyplot as plt
    # getA（）函数将矩阵转化为数组
    # weights=wei.getA()
    # 加载数据
    dataMat,labelMat=loadDataSet()
    dataArr=np.array(dataMat)
    # print(dataArr)
    n=np.shape(dataArr)[0]
    xcord1=[]
    ycord1=[]
    xcord2=[]
    ycord2=[]
    # print(labelMat)
    for i in range(n):
        if int(labelMat[i])==1:
            xcord1.append(dataArr[i][1])
            ycord1.append(dataArr[i][2])
        else:
            xcord2.append(dataArr[i][1])
            ycord2.append(dataArr[i][2])
    fig=plt.figure()
    ax=fig.add_subplot(111)
    # print(xcord1)
    # print(ycord1)
    ax.scatter(xcord1,ycord1,s=30,c='red',marker='s')
    ax.scatter(xcord2,ycord2,s=30,c='green')
    # arange()函数用于创造等差数组
            # 起始点 终止点 步长
    x=np.arange(-3.0,3.0,0.1)
    y=(-weights[0]-weights[1]*x)/weights[2]
    ax.plot(x,y)
    # 添加xy轴标签
    plt.xlabel('X1')
    plt.ylabel('X2')
    # 显示图像
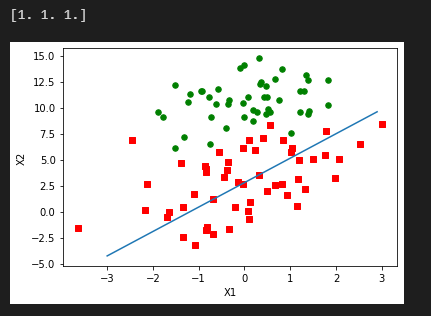
    plt.show()

调用上述函数：

print(type(weight))
weight=weight.getA()
plotBestFit(weight)

得到的输出结果为：

这个分类的结果还是不错的，从图上可以看到只有两三个点分错了。但是，尽管例子简单且数据集很小，这个方法却需要大量的计算（300次乘法）。因此下一节将对该算法稍作改进，从而使他可以应用于真正的数据集上  

 2.4 训练算法：随机梯度上升

梯度上升算法在每次更新回归系数时都需要遍历整个儿数据集，该方法在处理100个左右的数据集时尚可，但如果有数十亿样本和成千上万个特征，改方法的计算复杂度就太高了。一种改进方法是一次仅用一个样本点来更新回归系数，该方法称为随机梯度上升法。由于可以在新样本到来时进行增量式更新，因而随机梯度上升算法算是一个在线学习。与在线学习相对应，一次处理所有数据可以被称为“批处理”

伪代码如下：  

所有回归系数初始化为1  

对数据集中每个样本  

    计算该样本的梯度  

    使用alpha*gradient更新回归值系数值  

返回回归系数值  

 相关代码如下：

# 随机梯度上升法
def stocGradAscent0(dataMatrix,classLabels):
    dataMatrix=np.array(dataMatrix)
    # 不需要进行矩阵的转换
    m,n=np.shape(dataMatrix)
    # 移动步长加大
    alpha=0.01
    weights=np.ones(n)
    print(weights)
    for i in range(m):
        # 不是数值的计算，而是向量的计算
        h=sigmoid(sum(dataMatrix[i]*weights))
        error=classLabels[i]-h
        weights=weights+alpha*error*dataMatrix[i]
    return weights

调用上述代码：

dataArr,labelMat=loadDataSet()
weights=stocGradAscent0(dataArr,labelMat)
plotBestFit(weights)

得到的输出结果如下：

可以看出来，拟合出来的直线效果还不错，但并不如梯度上升法的直线效果那样完美，因为这里的分类器错分了大概有三分之一的样本

但是该算法由于有部分不能正确分类的样本点，在每次迭代的时候会引发系数的剧烈改变。我们期望算法能够避免来回波动，从而收敛到某个值，此外收敛速度也需要加快。

改进的随机梯度上升法如下：

# 改进的随机梯度上升法 使收敛速度更快
                                        #  迭代次数
def stocGradAscent1(dataMatrix,classLabels,numIter=150):
    import random
    dataMatrix=np.array(dataMatrix)
    m,n=np.shape(dataMatrix)
    weights=np.ones(n)
    for j in range(numIter):
        dataIndex=list(range(m))
        for i in range(m):
            # alpha每次迭代时需要调整 缓解数据波动或高频波动
            alpha=4/(1.0+j+i)+0.01
            # 随机选取样本更新回归系数，减少周期性波动
            randIndex=int(random.uniform(0,len(dataIndex)))
            # print(randIndex)
            h=sigmoid(sum(dataMatrix[randIndex]*weights))
            error=classLabels[randIndex]-h
            weights=weights+alpha*error*dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights

 调用上述代码：

weights=stocGradAscent1(dataArr,labelMat)
plotBestFit(weights)

得到的输出结果如下：

 3 示例：从疝气病症预测病马的死亡率

本节将使用logistic回归来预测有疝气病的马的存活问题。这里的数据包含了368个样本和28个特征。  

①收集数据：给定数据文件  

②准备数据：用python解析文本文件并填充缺失值  

③分析数据：可视化并观察数据  

④训练算法：使用优化算法，找到最佳系数  

⑤测试算法：为了量化回归的效果，需要观察错误率。根据错误率决定是否回退到训练阶段，通过改变迭代的次数和步长等参数来得到更好的回归系数  

⑥使用算法：实现一个简单的命令行程序来收集马的症状并输出预测结果并非难事  

3.1 准备数据：处理数据中的缺失值

数据中存在缺失值可处理的方法：  

①使用可用特征的均值来填补缺失值  

②使用特殊值来填补缺失值，如-1  

③忽略有缺失值的样本  

④使用相似样本的均值来填补缺失值  

⑤使用另外的机器学习算法来预测缺失值  

对数据集进行预处理，首先，所有的缺失值必须用一个实数值来替换。其次，如果在测试数据集中发现了一条数据的类别标签已经缺失，简单做法就是丢弃该数据

3.2 测试算法：用logistic回归进行分类

# 如果预测的sigmoid值大于0.5就属于第一个类别，否则就属于第二个类别
            #    回归系数 特征向量
def classifyVector(inX,weights):
    prob=sigmoid(sum(inX*weights))
    # print(prob)
    if prob>0.5:
        return 1.0
    else:
        return 0.0

# 打开测试集和训练集
def colicTest():
    # 读取文件
    frTrain=open('horseColicTraining.txt')
    frTest=open('horseColicTest.txt')
    trainingSet=[]
    trainingLabels=[]
    # 按行读取训练集文件
    for line in frTrain.readlines():
        currLine=line.strip().split('\t')
        lineArr=[]
        # 读取每行的22个数据
        for i in range(21):
            lineArr.append(float(currLine[i]))
        # 特征
        trainingSet.append(lineArr)
        # 标签为最后一个数据
        trainingLabels.append(float(currLine[21]))
    # 计算回归系数向量   可自由设置迭代次数
    trainWeights=stocGradAscent1(np.array(trainingSet),trainingLabels,500)
    # print(trainWeights)
    errorCount=0
    numTestVec=0.0
    # 读取测试集文件
    for line in frTest.readlines():
        # print(line)
        numTestVec+=1.0
        currLine=line.strip().split('\t')
        lineArr=[]
        for i in range(21):
            lineArr.append(float(currLine[i]))
        # print(lineArr)
        if int(classifyVector(np.array(lineArr),trainWeights))!=int(float(currLine[21])):
            # print(int(float(currLine[21])))
            errorCount+=1
    # 计算错误率
    errorRate=(float(errorCount)/numTestVec)
    # print(errorCount,numTestVec,errorRate)
    print('the error rate of this test is :%f' % errorRate)
    # 返回错误率
    return errorRate

def multTest():
    numTests=10
    errorSum=0.0
    # 调用十次colivTest函数，并且求得平均值，得到最终结果
    for k in range(numTests):
        errorSum+=colicTest()
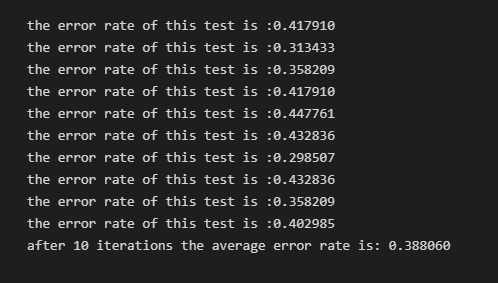
    print('after %d iterations the average error rate is: %f' % (numTests,errorSum/float(numTests)))

调用上述代码：

multTest()

得到的输出结果：

 4 本章小结

logistic的目的是寻找一个非线性sigmoid的最佳拟合函数，求解过程可以用最优化算法来完成