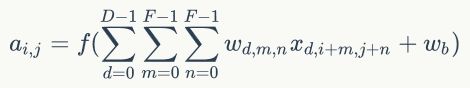卷积神经网络(Convolutional Neural Network, CNN)
https://www.zhihu.com/question/52237725/answer/545340892
神经元 neurons
1. 生物神经网络,通过刺激形成新的连接,信号通过新的连接传递而形成反馈。
人工神经网络,所有神经元之间的连接都是固定不可更换的,不可凭空产生新连接。
2. 依靠正向和反向传播,形成更好的神经系统。
3. 把神经元设计成三个维度: width, height, depth(描述神经元)。
eg. 输入图片大小32*32*3(rgb) =》 输入神经元:维度 32*32*3
CNN: a set of pixels -> a set of votes
1. 前馈神经网络。
2. 由具有可学习的 weights & biases 的神经元组成。(每个神经元都接收一些输入,并做点积计算,输出是每个分类的分数)。
3. 卷积:不对输入的每个pixel处理,而是对每一小块像素区域的处理。加强了图片信息的连续性。通过批量过滤器,不断滚动,收集图片信息(每次一小块区域),
4. 黑白图片,高维1;彩色图片具有RGB三原色,每一个pixel都有三层面RGB参数(作为厚度)。不断压缩长和宽,增加厚度。通过厚度里的信息,Full connection =》 分类器classifier
5. 卷积层不压缩长宽,避免图像重要信息丢失;通过pooling层,处理卷积后的信息并压缩。接上两层的FULLY CONNECTED 和classifier层作分类预测。
patch/kernel: 从图片中抽离的一个小部分
stride:每次跨多少步抽离图片中的一小部分像素点。eg. stride=1,每跨一个pixel抽离一次
抽取方式: walid padding(抽出来的比原先的长和宽被裁剪,在原图片内部); same padding(与原图长宽一致,某部分在图片外面,以零填充)
pooling: 跨度过长,导致图片重要信息丢失,故而加1层(stride=1),再用pooling的方法(max pooling\average pooling)压缩。
CNN vs 普通神经网络full connected
普通神经网络把input layer和hidden layer进行 full Connected 设计,从整幅图像中计算特征。
但对于较大的图像,将变得非常耗时。
eg. 对96*96的图像,需设计10^4个输入单元,假设要学习100个特征,则有10^6个参数需要学习。与28*28小块图像相比,96*96的图像使用 前向输送 或 后向传导 计算方式,计算过程慢10^2倍。
=》 卷积层:每个隐含单元仅仅连接输入图像的一小片相邻区域(神经元的感受野 receptive field)。
值的计算方法没有变,weights 和 input的点积,加上biases。
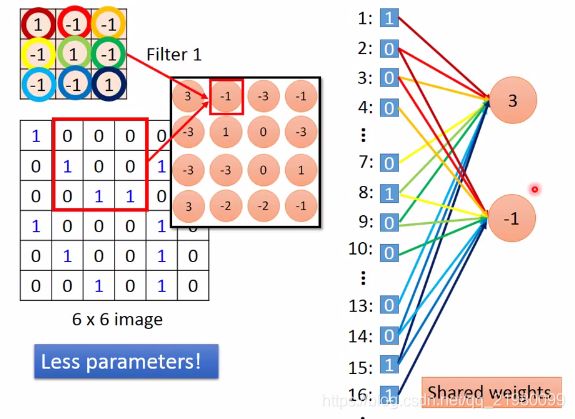
convolution:拿掉了full connection 中的一些weight. (less parameter)
eg: 如上图,output的3 只与1,2,3,7,8,9,13,14,15位置相关 => 9个不同的weight
CNN特点
1. 局部感知:感受野
每次卷积核所覆盖的像素只是一小部分(局部特征)
局部 =》整体(full connected)
2. 权重共享
整个图片共享一组filter参数
3. 多卷积核
一种卷积核代表一种特征。
组成
1. 卷积层 Convolutional layer
每层卷积层由若干卷积单元(参数:反向传播算法优化得到)组成。
目的:提取输入的不同特征。(第一层:可能只能提取一些低级特征,如边缘、线条、角等;更多层的网络能从低级特征中迭代提取更复杂的特征)。
卷积层的参数包含一系列过滤器(filter,特征提取器),每个过滤器训练一个depth,有几个过滤器输出单元就具有多少depth。
2. 线性整流层 Rectified Linear Units layer
activation function (ReLU)
3. 池化层 Pooling layer
降维(将特征切成几个区域,取其最大值或平均值,得到新的、维度较小的特征)。
4. 全连接层 Fully-Connected layer
把所有局部特征结合变成全局特征,用来计算最后每一类的得分。
process
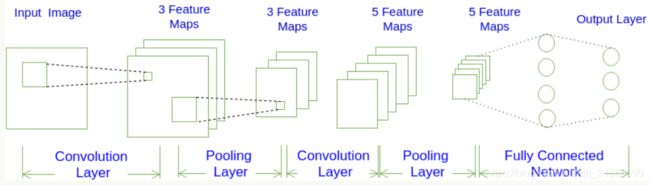
1. 输入层的宽度和高度对应于输入图像的宽度和高度,深度为1;
2. 第一个卷积层对这幅图像进行了卷积操作,得到了三个Feature Map(超参数:filter=3)。
Feature Map(通道(channel)):通过卷积变换提取到的图像特征,三个Filter就对原始图像提取出三组不同的特征。
3. Pooling层对三个Feature Map做下采样,得到了三个更小的Feature Map。
4. 第二个卷积层,有5个Filter。每个Filter都把前面下采样之后的3个Feature Map卷积在一起,得到一个新的Feature Map。接着,是第二个Pooling,继续对5个Feature Map进行下采样,得到了5个更小的Feature Map。
5. 最后两层是全连接层。
第一个全连接层的每个神经元,和上一层5个Feature Map中的每个神经元相连。
第二个全连接层(也就是输出层)的每个神经元,则和第一个全连接层的每个神经元相连,这样得到了整个网络的输出。
前面的卷积层和池化层是为了提取输入的高级特征,送到全连通层的输入,然后训练出最后的结果。
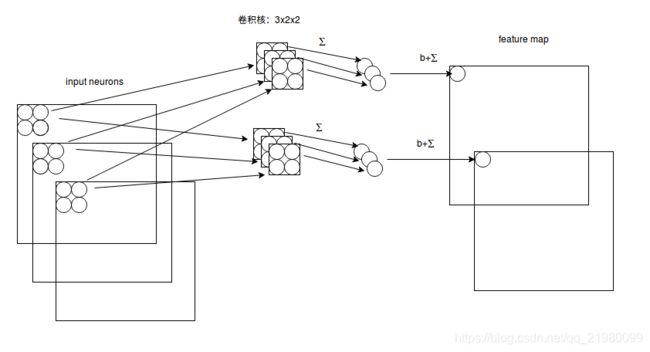
多通道多卷积核
输入有3个通道,同时有2个卷积核。对于每个卷积核,先在输入3个通道分别作卷积,再将3个通道结果加起来得到卷积输出。所以对于某个卷积层,无论输入图像有多少个通道,输出图像通道数总是等于卷积核数量!
对多通道图像做1x1卷积,其实就是将输入图像于每个通道乘以卷积系数后加在一起,即相当于把原图像中本来各个独立的通道“联通”在了一起。因此1x1卷积核可用来做降维处理。
空间排列 Spatial arrangement
深度 depth:控制输出单元的深度(filter个数),连接同一块区域的神经元个数。
步幅 stride:控制在同一depth的相邻两个隐含单元,与他们相连接的输入区域的距离。如果stride(=1)很小,相邻隐含单元的输入区域的重叠部分会很多;stride很大,则重叠区域少。
补零 zero-padding:通过在输入单元周围补零,改变输入单元大小,从而控制输出单元的空间大小。
1. 计算一个维度内一个输出单元里可以有几个隐藏单元(卷积后的Feature map宽度): ![]()
W:输入单元大小(卷积前宽度);F: 感受野(receptive field),Filter的宽度;S: stride;P: zero-padding 圈数的数量;K: depth
计算结果若不是一个整数 =》 stride不合适/ 需要zero-padding
参数共享 parameter sharing
假设:如果图像中的一点(x1, y1)包含的特征很重要,那么它应该和图像中的另一点(x2, y2)一样重要。
深度切片 depth slice: 同一深度的平面。同一个切片共享同一组weight & bias。
每个神经元连接数据窗的权重是固定的,每个神经元只关注一个特性(卷积层的每个滤波器都会有自己所关注一个图像特征,比如垂直边缘,水平边缘,颜色,纹理等等)。
卷积:一组固定的权重和不同窗口内数据做内积。
共享权值的梯度是所有共享参数的梯度的总和。
图片相似性:所有学习过程都是特征提取学习。
a neuron does not have to see the whole image to discover the pattern.
have the same parameter: the same patterns appear in different regions, but have the same mean and the same shape.
subsampling the pixels will not change the object
parameters:
filter matrix
超参数:
filter number
1. 经过变换后依然有某些特征是一致的, 故我们可以 将一个图片,分割成一个个小部分或特征,再匹配(filtering)。
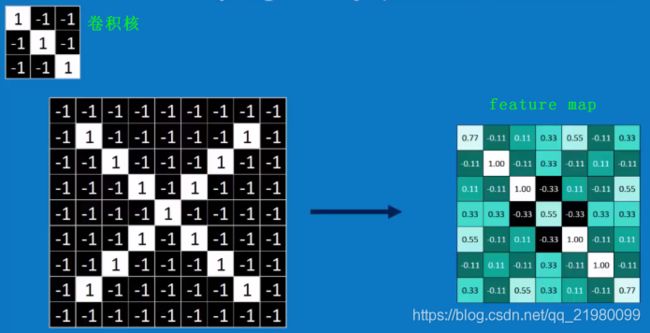
2.卷积核计算:移动filter到所有可能的位置,convolution(每个像素点内积,再除以总像素点数。 结果即为匹配程度,放在中心点)。提取出原图中(包含与卷积核一样的)特征提出出来。 image:9*9 =》7*7(几个filter,就有几个7*7image)
filter是检测斜对角,feature map中数值较高的都在对角线上,说明对角线上的与filter更匹配。
第二个conv layer : use 1st layer as module to build classifiers.
Normalization
激活函数ReLUs:negative->zero,收敛快。
a stack of images becomes a stack of images with no negative values.
经验:
1.不要用sigmoid
2. RELU
3. Leaky ReLU\Maxout
4. tanh
pooling(池化、下采样): shrinking the image stack
将误差项传递到上一层,而没有梯度的计算。
max pooling\average pooling: 降维的同时,依旧保留特征。 image:9*9=>7*7=>4*4
1. pick a window size(2\3).
2. pick a stride(2).
3. walk your window across your filtered images. 图像周围padding-zero:提取图像边缘特征。
4. from each window, take the maximum value.
对每个滑动窗口,选取最大值。将窗口向右移动一个stride,依次记录最大值。
=》降维,图片缩小一半(长宽均为原来一半)
Deep stacking
layers can be repeated several times(conv -> ReLU -> ……->pooling)
架构模式: INPUT -> [[CONV]*N -> POOL?]*M -> [FC]*K
N个卷积层叠加,然后(可选)叠加一个Pooling层,重复这个结构M次,最后叠加K个全连接层。
Fully connected layer:a list of feature values becomes a list of votes
将二维矩阵排成一列(flatten),丢到Fully Connected Feedforward network:每一个神经元乘以一定的权重,再加和。
every value gets a vote(depends on how strongly a value predicts X or O)
通过backpropagation与真实图片相比较,计算损失函数loss(反馈到第一个卷积核上,对卷积核参数修改)
目标:将损失函数降到最低 =》求导,得最小值 =》修改卷积核、神经元权重进行微调
Training
与全连接神经网络训练原理一致:利用链式求导计算损失函数对每个权重的偏导数(梯度),然后根据梯度下降公式更新权重。训练算法依然是反向传播算法(误差项=损失函数对神经元加权输入的偏导数)。
数据输入层
对原始图像数据预处理
1. 去均值
把输入数据各个维度都中心化为0(拉回到坐标系原点)。
2. 归一化
幅度归一化到同样的范围,减少各维度数据取值范围的差异而带来的干扰。
eg.有两个维度的特征A和B,A范围是0到10,而B范围是0到10000,如果直接使用这两个特征是有问题的,好的做法就是归一化,即A和B的数据都变为0到1的范围。
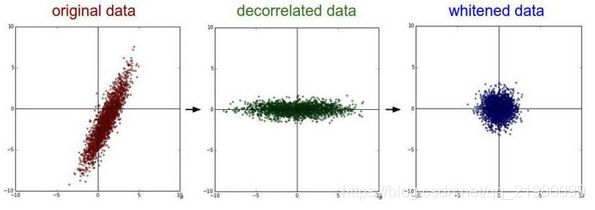
3. PCA/白化
用PCA降维;白化:对数据各个特征轴上的幅度归一化。
dropout:解决过拟合问题
神经网络的神经元过多,参数过多,导致训练集拟合得太好了。=》dropout一些神经元
在每个隐藏层的输入进行一个概率判决,eg.设置概率为0.5(keep_prob),生成一个跟隐藏层神经元个数相同大小的向量,true:false的比例是1:1(因为keep_prob=0.5),与隐藏层的输入进行相乘,那么会有一半隐藏层的神经元被丢掉,不起作用。
参考:https://www.zybuluo.com/hanbingtao/note/485480 (重要)
https://blog.csdn.net/qq_25762497/article/details/51052861
https://zhuanlan.zhihu.com/p/49184702?utm_source=wechat_session&utm_medium=social
https://www.bilibili.com/video/av35087157/?spm_id_from=333.788.b_7265636f5f6c697374.10
https://www.cnblogs.com/fydeblog/p/7450413.html
https://zhuanlan.zhihu.com/p/31426458