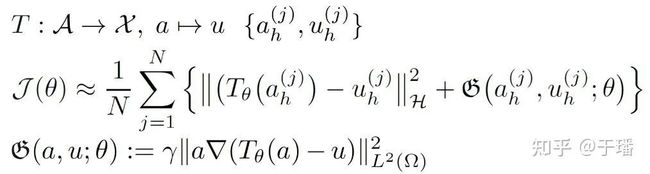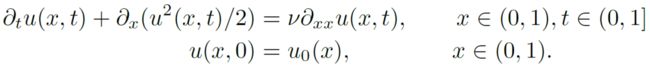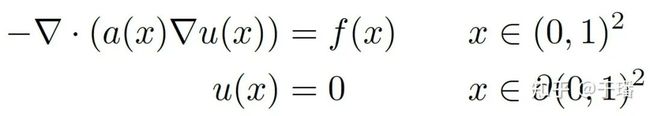当Transformer遇见偏微分方程求解

本篇与大家分享最近阅读的Transformer求解偏微分方程论文Choose a Transformer: Fourier or Galerkin，该论文已被NeurIPS2021接收。

背景介绍

在我们的世界中，从宇宙星体的运动，到温度风速的气象预报，再到分子原子间的相互作用，很多工程学、自然科学、经济和商业过程都可以通过偏微分方程（PDE）描述。传统的方法，如有限元、有限差分、谱方法等，利用离散结构将无限维算子映射简化为有限维近似问题。近年来物理信息神经网络（PINN）等模型[1]，通过在求解空间采样，训练神经网络来近似PDE解。但是对于传统方法或物理信息神经网络等，边界条件或者方程参数轻微的变化，通常需要重新计算和训练。

相比之下，算子学习的目标是学习无限维函数空间之间的映射，这样能够实现在不需要重新训练的情况下求解偏微分方程族，从而大幅度节省计算资源。PDE求解中算子学习（operator learner）是当前蓬勃发展的新研究方向，其中典型代表是傅里叶神经算子（FNO）[2]。

随着NeurIPS2021的放榜，基于Transformer的算子学习文章《Choose a Transformer: Fourier or Galerkin》[4]对于参数化PDE的求解给出了一种新颖的解释，最终在基准中取得了state-of-the-art的结果。

主要工作

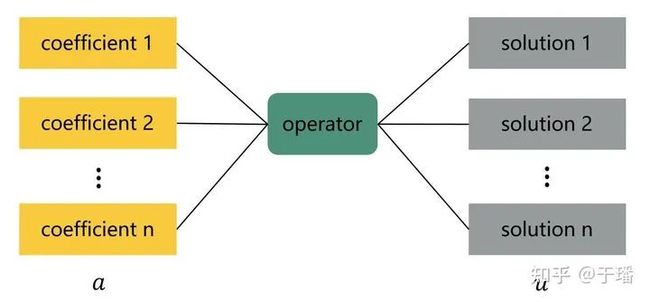
在本文中，operator learner采用监督学习训练，训练样本是输入函数和输出函数在同样的离散网格点上采样得到的，如下图所示，可以将方程求解转化seq2seq问题并通过Transformer[3]进行建模。

图1 operator learner示意

基于Transformer的工作，本文的主要贡献如下：

1. 无softmax的注意力机制。提出scale-preserving自注意机制和无softmax的attention，并给出两种方案的数学解释。

2. 参数化PDE的operator learner。将新提出的注意力算子与FNO结合起来，显著提高在参数化PDE求解基准问题中的精度。

3. State-of-the-art实验结果。在三个benchmark中，求解的精度和性能均有大幅度的收益。

Pipeline

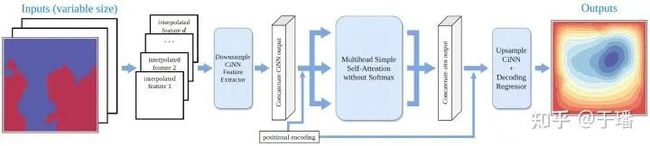
图2 二维operator learner网络结构

operator learner的网络结构如上图所示，其中主要包含如下几个模块：

1. 特征提取器（Feature extractor）：一维问题使用前馈神经网络、二维问题使用CNN网络等；

2. 基于插值的CNN（Interpolation-based CNN）：上采样/下采样层和CNN的堆叠得到；

3. 位置编码（Positional encoding）：每个网格点的笛卡尔坐标作为附加特征维连接到输入数据。

4. 解码器（Decoder）：编码器学习到的表示特征映射回原始维度。

其中网络训练的loss函数如下：

损失函数的主体为网络输出和label之间的MSEloss，另外loss中额外添加了输出和label之间差分正则项。

其中Fourier和Galerkin类型的Transformer计算方式如下图：

图3 Fourier Attention

图4 Galerkin Attention

实验结果

1. Burger’s equation

方程定义如下：

 

本文中的任务是从初始时刻（t=0）得到t=1时刻的解u，模型与FNO的对比如下表，在本问题上结果精度均优于所对比的FNO。

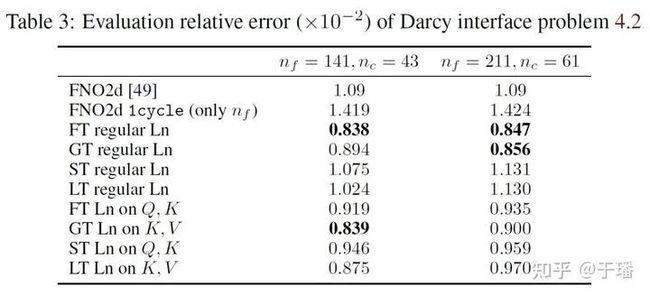
2. Darcy flow problem

方程定义如下：

该问题的定义是从二维的随机几何形状系数a，到二维的解u的映射。模型与FNO的对比如下表，在本问题上结果精度均优于所对比的FNO。

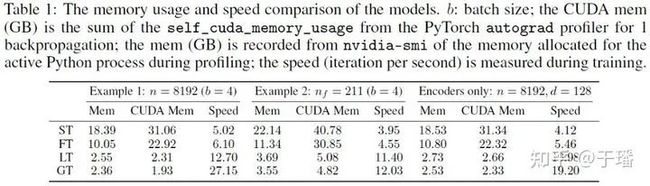
在对比模型精度的同时，论文也比较了模型的性能，对比结果如下表，其中Galerkin Attention方式的Transformer在显存占用和性能方面优势十分明显。

思考与总结

Galerkin Transformer从数学的角度解释了Attention机制，并新颖地将其与算子学习相结合引入到参数化PDE的求解问题中，精度和性能均优于算子学习的“老大哥”FNO。后续可以在更高维更复杂场景上，验证模型的有效性。

Reference

[1] Raissi M, Perdikaris P, Karniadakis G E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378: 686-707.

[2] Li Z, Kovachki N, Azizzadenesheli K, et al. Fourier neural operator for parametric partial differential equations[J]. arXiv preprint arXiv:2010.08895, 2020.

[3] Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[C]//Advances in neural information processing systems. 2017: 5998-6008.

[4] Cao S. Choose a Transformer: Fourier or Galerkin[J]. arXiv preprint arXiv:2105.14995, 2021.

MindSpore官方资料

GitHub : https://github.com/mindspore-ai/mindspore

Gitee : https : //gitee.com/mindspore/mindspore

官方QQ群 : 486831414