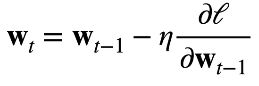1.1 pytorch深度学习--线性回归

前几章不管是安装软件还是关于线性代数和求导的数学教学，沐神都已经讲的很详细了。不详细的地方，我也说不出来个所以然，所以只能望诸君多多努力了。数据预处理部分很重要，但我还没彻底学明白，学明白后会补上。

此部分对于深度学习来说非常简单，但我个人认为对于初学者，尤其是对python不熟练的人来说至关重要。其不仅是机器学习最开始的地方，对初学者个人也是一个检验前几章是否学会弄懂，是否真正理解的地方。

在此之前的微积分部分，线性代数部分，理论可以点到为止，不求甚解，但通过代码的实现一定要清楚。本章也能对之前内容起到巩固作用，本人用泪换来的教训，如果有和我一样的初学者，一定要尝试纯手撸一遍这部分代码，并尽量保证把最关键部分的代码全部看懂。

生成数据集

线性回归的数学公式非常简单，

以买房子为例，假设只有房子的位置、房间数、房子面积这三个因素会影响房屋价格，并和房子价格线性相关。他们各自的权重为，对应的自变量可以是房子位置所在的繁华程度（例如从低到高分为10级，对应0-9）,房间数，房子面积。b可以最初认为假设为0。这就是公式在实际应用中的例子。

在这个模型中，我们能得到一组自变量X和对应的价格y，并希望通过这些数据确定权重w。

为了能验证之后学习的准确率，我们首先生成一组数据集，在此之前先确定为了完成这些工作需要导入哪些库。

import random
import torch
from matplotlib import plot as plt
from d2l import torch as d2l

d2l是沐神为了方便初学者，把一些简单但与课程主旨不太相关的东西（或者是讲过的内容）打包，方便调用。不过为了更好理解，之后我会尽量把调用的东西展开并尝试讲解。

假设总共1000组数据，数据集符合w = [2, -3.4]，b = 4.2，为了增加难度，加入噪声。如果还拿买房举例子，我认为这些噪音表示的可以是众多对房价影响很小的因素，例如房子颜色。和不可测因素，例如因为某人对某个房子（样本）单纯无理由的钟爱而出高价购买等。

def synthetic_data(w, b, num_examples):  #@save
    """生成y=Xw+b+噪声"""
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

 对用到的两个torch的函数做个解释

X = torch.normal(0, 1, (num_examples, len(w))) 
#正态分布，其中平均值是0，标准差是1，总共有num_examples*len(w)个数。
#shape=[num_examples, len(w)]"""
y = torch.matmul(X, w) + b
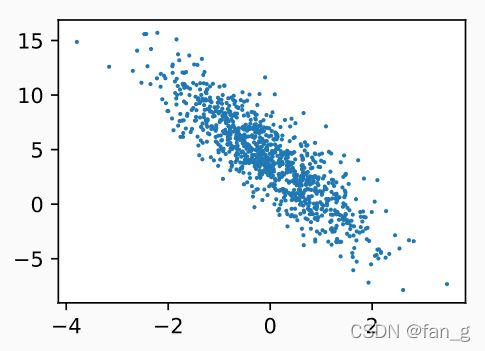
#matmul是叉乘，和数学公式一样，要注意X和w的shape，确定是[A,B]和[B,C]。

 通过散点图看两者关系

d2l.set_figsize()
"""
-----------------set_figsize()定义--------------------
def set_figsize(figsize=(3.5, 2.5)):
    use_svg_display()
    d2l.plt.rcParams['figure.figsize'] = figsize
------------------------------------------------------

---------------use_svg_display()定义------------------
def use_svg_display():
    display.set_matplotlib_formats('svg')
------------------------------------------------------
display在Ipython与matplotlib一起使用，这里确定了格式svg
第二句可以改成plt.subplots(1, 1, figsize=(3.5, 2.5))
表示总共一行一列一个图，如果只是一个图也可省略1，1。figsize
确定了图表的大小。
"""
plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1)
"""
scatter是点图，这里横坐标是特征值集的第二列，纵坐标是标签值
其中detach().numpy()将tensor类转成numpy的类。
"""

读取数据集

在确定数据集后，我们希望电脑能通过数据集得到w。因此，第一步是读取已创建好的数据集。尽管数据集越大，得到的w和b就更准确，但一次读取全部特征值集会占用大量的内存。除此以外还会导致大量不必要的计算，在损失函数和优化部分会展开说明。因此可以采取设置批量大小，分批次读取的方法。

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    """这些样本是随机读取的，没有特定的顺序
    shuffle可以打乱indices顺序，保证随机读取"""
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(indices[i: min(i + 
                        batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]
    
    """
    为了方便理解，我们首先假设num_examples非常大，因此
    batch_indices = torch.tensor(indices[i: i + batch_size])
    需要注意此时indices是乱序排列，即随机的一组数据而非连续的数据。
    yield在此处可先理解为return，即当得到features和labels后返回数
    据。
    """

当下次该函数再次被调用时，将会从yield后继续运行，即将读取i到i+batch_size的数据。当i+batch_size大于num_examples时，将只读取到最大值。这时批量值不等于设置的size值，但并不会影响结果。

关于field的用法网络上有很多，一些大神讲解的非常详细且精炼，在此放一篇，方便大家更详细的理解。

python中yield的用法详解——最简单，最清晰的解释

同时为了更深入的了解，还建议趁此机会对迭代等进行学习。

初始化模型参数

在确定读数据的方法之后，需要首先对参数进行初始化，即人为设置一个值。

w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

此处一定要注意w的size为(2,1)，如果写反则在叉乘过程中将出错。另外，因为之后要对此求导，进而通过随机梯度下降法，确定最终的w值和b值，所以要设置成requires_grad=True。

定义模型

def linreg(X, w, b):  #@save
    """线性回归模型"""
    return torch.matmul(X, w) + b

确定线性回归模型

定义损失函数

 

 该公式还可以进一步简化，假设X = [X, 1]，w = [w, b]。其中，X和y是定值，也就是说损失函数值只与w和b有关。当损失函数值对所有X和y都等于0时，我们可以说w和b就是该模型的解析解。但由于还存在噪声，该函数可能无法到0，因此需要确定优化算法，使得损失函数值最小。

需要注意的是，如果对所有数据求损失值将导致大量的计算，并在优化算法阶段对全部数据求导，这将产生非常大的计算量。因此我们可以选择一个批量求该批量的损失函数值，在合适大小下，这个值将近似于全部数据的损失函数。

def squared_loss(y_hat, y):  #@save
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

需要注意的是，与公式不同，此处并没有对均方损失除以批量大小，即损失所得结果不仅与w和b有关，还和批量大小有关。因此，在之后优化算法时，需要对此结果除以批量大小。

定义优化算法

尽管大多数人应该都已经了解在优化时一般选择小批量随机梯度下降，但为了更好的帮助理解，不得不再次提到梯度下降的一般公式。

如上所说，我们可以选择一个小批量数据并对其优化以近似对全部数据优化。

新的权重等于上一个权重减学习率乘损失函数的偏微分，注意，此处的w已包含b。在存在解析解的情况下，损失函数将最终等于0，我们可以说此时的w即为函数解析解。

通过小批量随机梯度下降公式，我们可以通过对随机选择的批量数据优化近似对全局优化。

def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

params = [w, b]，lr是learning rate，batch_size是批量大小。

此处torch.no_grade()是指对下面内容不再进行梯度计算。根据上面公式可以看出，对梯度计算的目的是计算损失函数对w（此处w = [w,b]）的偏微分，并将结果与w相减迭代出新w。此过程不需要梯度计算。

训练

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # X和y的小批量损失
        # 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起，
        # 并以此计算关于[w,b]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

 这部分是主要代码，可能看不懂的地方主要由两个。

第一个是将函数名赋给另一个名，例如net = linreg。这部分可以直接理解为是给函数起别名，本质上是把函数的地址赋给net。

第二个是sgd没有返回函数是怎么更新w的。首先说答案。赋给sgd函数的是w和b的地址，而不是他们的值。

验证：

def sgd(w, b, lr, batch_size):
    with torch.no_grad():
        # id即指针，在此处读w指针，并与主函数w对比。
        print(id(w))
        params = [w, b]
        # 在此处读params[0]的指针，与上一个w相比。
        print(id(params[0]))
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()


for epoch in range(num_epchs):
    for X, y in data_iter(batch_size, features, labels):
        y_hat = net(X, w, b)
        l = loss(y_hat, y)
        l.sum().backward()
        # 在此处读w的指针。
        print(id(w))
        sgd(w, b, lr, batch_size)
        # 在此处读w的指针,说明前后未变。
        print(id(w))
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')