神经网络学习（二）：解常微分方程

前言

        在完成了函数拟合之后，现在考虑常微分方程：给定一个常微分方程，让你求得这个微分方程的近似解（在给定的初值条件下）。以前都是用数学的知识来解决（这让我想起了大一在立人楼上常微分的夜晚），现在有了神经网络，我们用深度学习的方法来解决它试一试。

        本次选择的微分方程是，当然学过常微分的同学都知道这个函数的解是

训练流程

 1.定义网络

        本来是想使用之前定义的网络，但是觉得以后反正要用就规范化一下这个网络，增加一下可操作性（其实是因为当时我人在办公室笔记本上没有代码就直接重写了），在初始化中增加了2个参数NL和NN，可以控制你的网络是几层，每层多少个神经元，其他的都不变（总的来说也是借鉴了知乎大佬的文章：深度学习求解偏微分方程系列一：Deep Galerkin Method - 知乎）

class Net(nn.Module):
    def __init__(self, NL, NN):
        # NL是有多少层隐藏层
        # NN是每层的神经元数量
        super(Net, self).__init__()
        self.input_layer = nn.Linear(1, NN)
        self.hidden_layer = nn.ModuleList([nn.Linear(NN, NN) for i in range(NL)])
        self.output_layer = nn.Linear(NN, 1)

    def forward(self, x):
        o = self.act(self.input_layer(x))
        for i, li in enumerate(self.hidden_layer):
            o = self.act(li(o))
        out = self.output_layer(o)
        return out

2.定义损失

        这个就是跟上文不同的地方，之前是有数据的，而现在你只有一个方程，那么如何定义损失并进行优化呢？这里就要提到一篇文章提到的网络PINN，将微分方程放到一边作为近似函数，将函数不为0的部分纳入损失。其次，将初值条件纳入损失中。损失可以用下面的等式表示

        其中MSE是整个过程中产生的损失（也可以叫误差），是初值条件带来的损失，而是近似函数带来的损失，使MSE作为目标损失Loss，对其反向传播从而进行训练网络

        Mse1 = loss_fn(y_train,dx)
        Mse2 = loss_fn(y_0,torch.ones(1))
        loss = Mse1 + Mse2

       可以看到这里面出现了dx，其实这个dx就是，具体的求导结果是来自于torch包里的autograd，具体为

dx = torch.autograd.grad(net(x), x, grad_outputs=torch.ones_like(net(x)), create_graph=True)[0]

        右边求导的结果是取了第一维的，原因是右边的类型是tuple类型，不能直接用于后续计算（采坑点一）

3.选择优化器

        这里我选择了Adam来优化（因为它是我测试下来效果最好的）

optimizer = optim.Adam(net.parameters(),lr)

4.训练&可视化

        具体的方法是和第一篇文章差不多的，不过在这里选择了新的方法来做数据集（刚学会了函数unsqueeze()）

x = torch.linspace(0, 2, 2000,requires_grad=True).unsqueeze(-1)

        这样就不用像以前那样写的比较冗余，是不是很贴切，顺带一说，因为整个过程需要求导，所以对于自变量x我们需要加入参数requires_grad=True,这样才能使得后面能够正常求导

5.训练结果

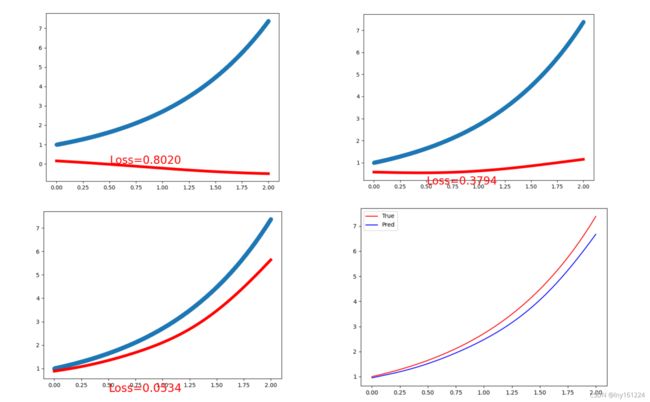
        本文我们设置了4层隐藏层，每层20个神经元，在该情况下得到的结果，为了对比，我也测试了（一）中的网络达到的效果。

 图1-用（一）中的网络结构得到的效果

 图2-用本文中的网络结构得到的效果

        可以看出来第二种的效果就比第一种要好一些，能够在更短的步数得到更好的效果，且带参数的网络可以使得我们随时调节隐藏层结构来满足不同要求

总结与展望

        利用深度学习来求常微分方程数值解，只要确定了近似函数和损失，就可以让网络慢慢去学习更新优化参数，最后获得比较满意的结果。这样一来，就降低了数学难度（但是数学基础确实很重要！）

        然后讲讲本次实验的采坑点吧，为了方便描述我就按点来列：

        a)求得dx并带入

                为了能够把导数带入公式我去学了一下autograd，然后用的时候吧，我就一直报错，就是因为那个Tuple类型，我debug的时候看他也就一维啊，寻思为啥，最后看了别人的解法我就直接取第一维就解决了

        b)损失的计算

                因为有了初值条件，损失比起上一篇多了一个求和的过程，别小看这一个求和，这俩可是两个不同维度的向量，所以要么你把零向量那个size选的和你x一样，这样直接相加；或者就是你把Loss_fn的参数设置为'mean’，这样就返回的标量，就没那么多问题了

        c)样本点以及样本范围

                本来我是以为我的模型或者计算出了什么问题，刚开始得到的模型结果一直都不好，直到偶然间我把样本范围从[0,5]改成了[0,2]效果立竿见影！原来就是我样本范围太大，指数函数变化太快学不过来导致后面效果不好的，所以发现模型不行，可能是你样本选的不好。

        d)激活函数

                不得不说，在我测试了这几个激活函数之后，还是tanh()效果最佳(tanh()永远滴神）

        接下来准备对偏微分方程进行模拟，给定了偏微分方程、初值条件、边界条件后，求方程的精确解。与本文的不同点是涉及到了偏导数，以及维度增加了，需要考虑到边界条件的处理，当然损失的计算也会更新，在下一篇会详细讲。

源代码

"""
用神经网络模拟微分方程,f(x)'=f(x),初始条件f(0) = 1
"""
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
import torch.optim as optim
from torch.autograd import Variable
class Net(nn.Module):
    def __init__(self, NL, NN):
        # NL是有多少层隐藏层
        # NN是每层的神经元数量
        super(Net, self).__init__()
        self.input_layer = nn.Linear(1, NN)
        self.hidden_layer = nn.ModuleList([nn.Linear(NN, NN) for i in range(NL)])
        self.output_layer = nn.Linear(NN, 1)

    def forward(self, x):
        o = self.act(self.input_layer(x))
        for i, li in enumerate(self.hidden_layer):
            o = self.act(li(o))
        out = self.output_layer(o)
        return out

    def act(self, x):
        return torch.tanh(x)
if __name__ == "__main__":
    x = torch.linspace(0, 2, 2000,requires_grad=True).unsqueeze(-1)
    y = torch.exp(x)
    net = Net(4, 20)
    lr = 1e-4
    loss_fn = nn.MSELoss(reduction='mean')
    optimizer = optim.Adam(net.parameters(),lr)
    plt.ion()
    for i in range(10 ** 4):

        y_0 = net(torch.zeros(1))
        dx = torch.autograd.grad(net(x), x, grad_outputs=torch.ones_like(net(x)), create_graph=True)[0]
        optimizer.zero_grad()
        y_train = net(x)
        Mse1 = loss_fn(y_train,dx)
        Mse2 = loss_fn(y_0,torch.ones(1))
        loss = Mse1 + Mse2
        if i % 2000 == 0:
            plt.cla()
            plt.scatter(x.detach().numpy(),y.detach().numpy())
            plt.plot(x.detach().numpy(), y_train.detach().numpy(), c='red',lw=5)
            plt.text(0.5, 0, 'Loss=%.4f' % loss.item(), fontdict={'size': 20, 'color': 'red'})
            plt.pause(0.1)
            print(f'times {i} - lr {lr} -  loss: {loss.item()} - y_0: {y_0}')
        loss.backward()
        optimizer.step()
    plt.ioff()
    plt.show()
    y_1 = net(torch.ones(1))
    print(f'y_1:{y_1}')
    y2 = net(x)
    plt.plot(x.detach().numpy(), y.detach().numpy(), c='red', label='True')
    plt.plot(x.detach().numpy(), y2.detach().numpy(), c='blue', label='Pred')
    plt.legend(loc='best')

    plt.show()

相关阅读

PINNs:https://github.com/maziarraissi/PINNs

当神经网络遇上物理: PINNs原理解析 - 知乎1. 简介大多数物理规律都可以表述为偏微分方程(PDE)的形式。偏微分方程，尤其是高阶偏微分方程难以求解析解，通常是采用各种方式逼近从而获得近似解。而神经网络的强大之处就在于其是万能近似器(universal approxi…https://zhuanlan.zhihu.com/p/363043437