0-1规划模型 Python
我们直接从题目入手学习0-1规划模型。
问题一:

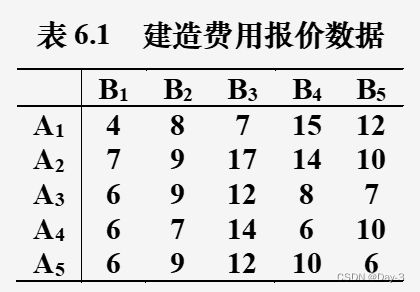
可以看出,这是一个标准的指派问题。引进0-1变量。

建立数学模型得:

import cvxpy as cp
import numpy as np
c = np.array([[4,8,7,15,12],
[7,9,17,14,10],
[6,9,12,8,7],
[6,7,14,6,10],
[6,9,12,10,6]])
x = cp.Variable((5,5),integer = True)
obj = cp.Minimize(cp.sum(cp.multiply(c,x)))
con = [0 <= x, x <= 1, cp.sum(x, axis = 0, keepdims = True) == 1,
cp.sum(x, axis = 1, keepdims = True) == 1]
prob = cp.Problem(obj, con)
prob.solve(solver = 'GLPK_MI')
print("最优值为", prob.value)
print("最优解为:", x.value)
问题二:选修课策略问题
某学校规定,运筹学专业的学生毕业时必须至少学习过两门数学课、三门运筹学课和两门计算机课。这些课程的编号、名称、学分、所属类别和先修课要求如表1所示。
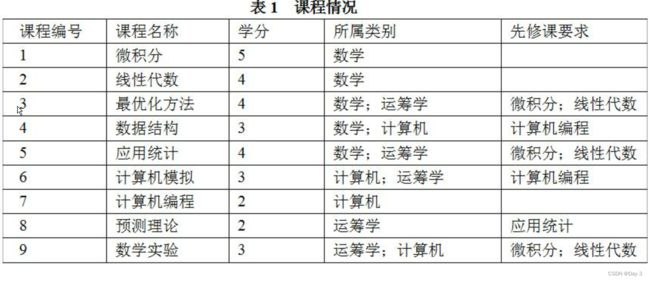
问题:毕业时学生最少可以学习这些课程中哪些课程。
如果某个学生既希望选修课程的数量少,又希望所获得的学分多,他可以选修哪些课程。
模型的建立:
1.不考虑学分情形
记 i = 1 , 2 , ⋯ , 9 i=1,2,\cdots,9 i=1,2,⋯,9表示九门课程的编号。设 x i = 1 x_{i} = 1 xi=1表示第 i i i门课程选修, x i = 0 x_{i} = 0 xi=0表示第i门课程不选。问题的目标为选修的课程总数最少,即:
min Z = ∑ i = 1 9 x i \min Z=\sum_{i=1}^{9}x_{i} minZ=∑i=19xi
约束条件包括两个方面:
第一个方面是课程数量的约束:
每个人至少要学习两门数学课,则 x 1 + x 2 + x 3 + x 4 + x 5 ≥ 2 x_{1}+x_{2}+x_{3}+x_{4}+x_{5} \ge 2 x1+x2+x3+x4+x5≥2
每个人至少要学习三运筹学课,则 x 3 + x 5 + x 6 + x 8 + x 9 ≥ 3 x_{3}+x_{5}+x_{6}+x_{8}+x_{9} \ge 3 x3+x5+x6+x8+x9≥3
每个人至少要学习两门计算机课,则 x 4 + x 6 + x 7 + x 9 ≥ 2 x_{4}+x_{6}+x_{7}+x_{9} \ge 2 x4+x6+x7+x9≥2
第二方面是先修课程的关系约束:
“最优化方法”的先修课是“微积分”和“线性代数”,有: x 3 ≤ x 1 , x 3 ≤ x 2 x_{3} \le x_{1},x_{3}\le x_{2} x3≤x1,x3≤x2
“数据结构”的先修课程是“计算机编程”,有: x 4 ≤ x 7 x_{4}\le x_{7} x4≤x7
“应用统计”的先修课是“微积分”和“线性代数”,有: x 5 ≤ x 1 , x 5 ≤ x 2 x_{5}\le x_{1},x_{5}\le x_{2} x5≤x1,x5≤x2
“计算机模拟”的先修课程是“计算机编程”,有: x 6 ≤ x 7 x_{6}\le x_{7} x6≤x7
“预测理论”的先修课程是“应用统计”,有: x 8 ≤ x 5 x_{8} \le x_{5} x8≤x5
“数学实验”是“微积分”和“线性代数”,有: x 9 ≤ x 1 , x 9 ≤ x 2 x_{9}\le x_{1},x_{9}\le x_{2} x9≤x1,x9≤x2
总的0-1规划模型为:
min Z = ∑ i = 1 9 x i s.t. { x 1 + x 2 + x 3 + x 4 + x 5 ≥ 2 x 3 + x 5 + x 6 + x 8 + x 9 ≥ 3 x 4 + x 6 + x 7 + x 9 ≥ 2 x 3 ≤ x 1 , x 3 ≤ x 2 x 4 ≤ x 7 x 5 ≤ x 1 , x 5 ≤ x 2 x 6 ≤ x 7 x 8 ≤ x 5 x 9 ≤ x 1 , x 9 ≤ x 2 x 1 , x 2 , ⋯ , x 9 = 0 或 1 \begin{array}{l} \min Z=\sum_{i=1}^{9} x_{i} \\ \text { s.t. }\left\{\begin{array}{l} x_{1}+x_{2}+x_{3}+x_{4}+x_{5} \geq 2 \\ x_{3}+x_{5}+x_{6}+x_{8}+x_{9} \geq 3 \\ x_{4}+x_{6}+x_{7}+x_{9} \geq 2 \\ x_{3} \leq x_{1}, x_{3} \leq x_{2} \\ x_{4} \leq x_{7} \\ x_{5} \leq x_{1}, x_{5} \leq x_{2} \\ x_{6} \leq x_{7} \\ x_{8} \leq x_{5} \\ x_{9} \leq x_{1}, x_{9} \leq x_{2} \\ x_{1}, x_{2}, \cdots, x_{9}=0 \text { 或 } 1 \end{array}\right. \end{array} minZ=∑i=19xi s.t. ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧x1+x2+x3+x4+x5≥2x3+x5+x6+x8+x9≥3x4+x6+x7+x9≥2x3≤x1,x3≤x2x4≤x7x5≤x1,x5≤x2x6≤x7x8≤x5x9≤x1,x9≤x2x1,x2,⋯,x9=0 或 1
import cvxpy as cp
import numpy as np
c = np.array([1,1,1,1,1,1,1,1,1])
x = cp.Variable(9,integer = True)
A = array([[-1,-1,-1,-1,-1,0,0,0,0],
[0,0,-1,0,-1,-1,0,-1,-1],
[0,0,0,-1,0,-1,-1,0,-1],
[-1,0,1,0,0,0,0,0,0],
[0,-1,1,0,0,0,0,0,0],
[0,0,0,1,0,0,-1,0,0],
[-1,0,0,0,1,0,0,0,0],
[0,-1,0,0,1,0,0,0,0],
[0,0,0,0,0,1,-1,0,0],
[0,0,0,0,-1,0,0,1,0],
[-1,0,0,0,0,0,0,0,1],
[0,-1,0,0,0,0,0,0,1]])
b = array([-2,-3,-2,0,0,0,0,0,0,0,0,0])
obj = cp.Minimize(cp.sum(cp.multiply(c,x)))
con = [A * x <= b, 0 <= x, x <= 1]
prob = cp.Problem(obj, con)
prob.solve(solver = 'GLPK_MI')
print("最优值为", prob.value)
print("最优解为:", x.value)
2.考虑学分情形
此时总的双目标0-1规划模型为:
min Z 1 = ∑ i = 1 9 x i max Z 2 = ∑ i = 1 9 c i x i \begin{array}{l} \min Z_{1}=\sum_{i=1}^{9} x_{i} \\ \max Z_{2}=\sum_{i=1}^{9} c_{i} x_{i} \end{array} minZ1=∑i=19ximaxZ2=∑i=19cixi
我们这里采取先计算上选修课数量最少,再去求解学分最高。
import cvxpy as cp
import numpy as np
from numpy import array
c = np.array([-5,-4,-4,-3,-4,-3,-2,-2,-3])
A = array([[-1,-1,-1,-1,-1,0,0,0,0],
[0,0,-1,0,-1,-1,0,-1,-1],
[0,0,0,-1,0,-1,-1,0,-1],
[-1,0,1,0,0,0,0,0,0],
[0,-1,1,0,0,0,0,0,0],
[0,0,0,1,0,0,-1,0,0],
[-1,0,0,0,1,0,0,0,0],
[0,-1,0,0,1,0,0,0,0],
[0,0,0,0,0,1,-1,0,0],
[0,0,0,0,-1,0,0,1,0],
[-1,0,0,0,0,0,0,0,1],
[0,-1,0,0,0,0,0,0,1],
[1,1,1,1,1,1,1,1,1]])
b = array([-2,-3,-2,0,0,0,0,0,0,0,0,0,6])
x = cp.Variable(9,integer = True)
obj = cp.Minimize(c*x)
con = [A * x <= b, 0 <= x, x <= 1]
prob = cp.Problem(obj, con)
prob.solve(solver = 'GLPK_MI')
print("最优值为", -prob.value)
print("最优解为:", x.value)
鉴于笔者水平有限,疏漏难所在免,欢迎指正错误!