第十三届蓝桥杯JavaB组国赛H题——修路 (AC)
目录
- 1.修路
-
- 1.问题描述
- 2.输入格式
- 3.输出格式
- 4.样例输入
- 5.样例输出
- 6.数据范围
- 7.原题链接
- 2.解题思路
- 3.Ac_code
1.修路
1.问题描述
这天, 小明在修路。
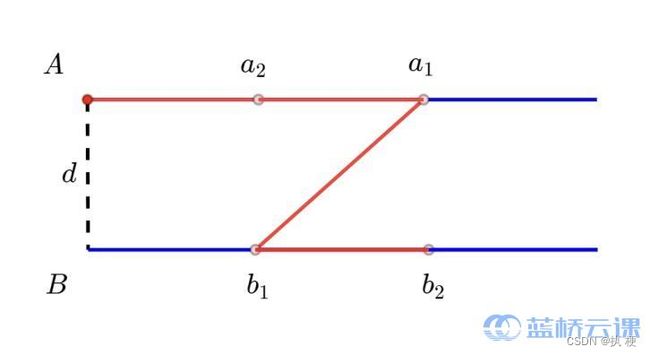
他需要修理两条平行的道路 A , B A, B A,B, 两条路上面分别有 n n n 个和 m m m 个点需要 维脩, 它们相对于道路起点的距离分别为 a 1 , a 2 , … , a n a_{1}, a_{2}, \ldots, a_{n} a1,a2,…,an 和 b 1 , b 2 , b , … , b m = b_{1}, b_{2}, b, \ldots, b_{m}= b1,b2,b,…,bm= 如图, 两条路之间的距离为 d d d 且它们起点 (最左端) 的连线和两条路都垂直。小明的起 点为道路 A A A 的起点, 他需要尽可能快地逆历这些需要维修的 n + m n+m n+m 个点, 他既 可以沿着道路 向右行走, 也可以在两条道路之间的空地上随意行走。
小明想知道遍历这些点的最短路程是多少。
2.输入格式
输入共三行,第一行为三个正整数 n , m , d n, m, d n,m,d 。
第二行为 n n n 个由空格㤱开的正整数 a 1 , a 2 , … , a n a_{1}, a_{2}, \ldots, a_{n} a1,a2,…,an。
第三行为 m m m 个由空格隔开的正整数 b 1 , b 2 , … , b m b_{1}, b_{2}, \ldots, b_{m} b1,b2,…,bm。
3.输出格式
一行, 一个浮点数, 表示答案, 保留两位小数。
4.样例输入
2 2 2
2 1
1 2
5.样例输出
5.24
图中红线指出了样例的最短路线, 1 + 1 + 5 + 1 = 5.24 1+1+\sqrt{5}+1=5.24 1+1+5+1=5.24 。
6.数据范围
保证 n , m ≤ 2000 , d ≤ 4 × 1 0 6 , a i , b i ≤ 1 0 6 。 n, m \leq 2000, d \leq 4 \times 10^{6}, a_{i}, b_{i} \leq 10^{6}。 n,m≤2000,d≤4×106,ai,bi≤106。
7.原题链接
修路
2.解题思路
考虑使用 d p dp dp 解决问题,设 f [ i ] [ j ] [ k ] f[i][j][k] f[i][j][k] 为道路 A A A 走过前 i i i 个点,道路 B B B 走过前 j j j 个点,当 k k k 为0时最终停在道路 A A A , k k k 为1时最终停在道路 B B B 的 最短距离。
考虑 d p dp dp 的初始化,因为起点是 A A A 道路的端点,所以对于所有的 f [ i ] [ 0 ] [ 0 ] f[i][0][0] f[i][0][0]的值就为 A [ i ] A[i] A[i] , f [ i ] [ 0 ] [ 1 ] f[i][0][1] f[i][0][1] 是一类非法状态,因为走过 B B B 道路的点数为 0 0 0 时 k k k 的状态不可能为1,所以我们需要初始化为无穷大。对于 f [ 0 ] [ i ] [ 0 ] f[0][i][0] f[0][i][0] 和 f [ 0 ] [ i ] [ 1 ] f[0][i][1] f[0][i][1] 的初始化同理, f [ 0 ] [ i ] [ 0 ] f[0][i][0] f[0][i][0]为非法状态,初始化为正无穷, f [ 0 ] [ i ] [ 1 ] f[0][i][1] f[0][i][1] 和上面有点不同,它的值应该是 B [ i ] − B [ 1 ] B[i]-B[1] B[i]−B[1]再加上起点到 B [ 1 ] B[1] B[1] 的距离,所以我们先预处理得到起点到 B [ 1 ] B[1] B[1] 的距离,我们称之为sb。
这里需要注意的, B [ 1 ] B[1] B[1]指的是道路 B B B最左边的点,题目给定的点并不是有序的,所以我们需要先对 A A A 和 B B B 道路的点进行排序。
然后考虑状态转移:
对于 f [ i ] [ j ] [ 0 ] f[i][j][0] f[i][j][0] ,说明此时我们停留在点 A [ i ] A[i] A[i] 上,它可以从道路 A A A 的上一个点转移过来,也可能是从对面的点 B [ j ] B[j] B[j] 走过来,对于两种状态我们应该去一个min作为答案,转移方程为:
f [ i ] [ j ] [ 0 ] = m i n ( f [ i − 1 ] [ j ] [ 0 ] + A [ i ] − A [ i − 1 ] , f [ i − 1 ] [ j ] [ 1 ] + d i s ( A [ i ] , B [ j ] , d ) ) f[i][j][0]=min(f[i-1][j][0]+A[i]-A[i-1],f[i-1][j][1]+dis(A[i],B[j],d)) f[i][j][0]=min(f[i−1][j][0]+A[i]−A[i−1],f[i−1][j][1]+dis(A[i],B[j],d))
f [ i ] [ j ] [ 1 ] f[i][j][1] f[i][j][1],说明我们此时停留在 B [ j ] B[j] B[j] 上,同样分析它可以从对面 A [ i ] A[i] A[i] 走过来,也可能从道路 B B B 的上一个点走过来,两种状态取一个min作为答案,转移方程:
f [ i ] [ j ] [ 1 ] = m i n ( f [ i ] [ j − 1 ] [ 1 ] + B [ j ] − B [ j − 1 ] , f [ i ] [ j − 1 ] [ 0 ] + d i s ( A [ i ] , B [ j ] , d ) ) ; f[i][j][1]=min(f[i][j-1][1]+B[j]-B[j-1],f[i][j-1][0]+dis(A[i],B[j],d)); f[i][j][1]=min(f[i][j−1][1]+B[j]−B[j−1],f[i][j−1][0]+dis(A[i],B[j],d));
最终的答案应该为 f [ n ] [ m ] f[n][m] f[n][m],代表我们走完所有的点,但是并不确定结束时我们是站在道路 A A A还是道路 B B B上,所以答案在 f [ i ] [ j ] [ 0 ] f[i][j][0] f[i][j][0]和 f [ i ] [ j ] [ 1 ] f[i][j][1] f[i][j][1]取更小值。
dis函数用于求斜线距离,基于三角形的勾股定理。
时间复杂度: O ( n m ) O(nm) O(nm)。
3.Ac_code
import java.io.*;
import java.util.Arrays;
public class Main {
static int N = 2010;
static int n, m;
static int d;
static int[] A = new int[N], B = new int[N];
static double[][][] f = new double[N][N][2];
static int inf = 0x3f3f3f3f;
static BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static void main(String[] args) throws IOException {
String[] s=br.readLine().split(" ");
n = Integer.parseInt(s[0]);
m = Integer.parseInt(s[1]);
d = Integer.parseInt(s[2]);
s=br.readLine().split(" ");
for (int i = 1; i <= n; ++i) A[i] = Integer.parseInt(s[i-1]);
s=br.readLine().split(" ");
for (int i = 1; i <= m; ++i) B[i] = Integer.parseInt(s[i-1]);
Arrays.sort(A, 1, n + 1);
Arrays.sort(B, 1, m + 1);
double sb = dis(B[1], 0, d);
for (int i = 1; i <= n; ++i) {
f[i][0][0] = A[i];
f[i][0][1] = inf;
}
//遍历下面
for (int i = 1; i <= m; ++i) {
f[0][i][1] = sb + B[i] - B[1];
f[0][i][0] = inf;
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
f[i][j][0] = Math.min(f[i - 1][j][0] + A[i] - A[i - 1], f[i - 1][j][1] + dis(A[i], B[j], d));
f[i][j][1] = Math.min(f[i][j - 1][1] + B[j] - B[j - 1], f[i][j - 1][0] + dis(A[i], B[j], d));
}
}
double ans = Math.min(f[n][m][0], f[n][m][1]);
out.printf("%.2f", ans);
out.flush();
}
static double dis(long x, long y, double w) {
return Math.sqrt((x - y) * (x - y) + w * w);
}
}