参考线平滑-FemPosDeviation-Ipopt

参考线平滑-FemPosDeviation-Ipopt

FemPosDeviation参考线平滑方法是离散点平滑方法，Fem是Finite element estimate的意思。
Apollo中使用Ipopt求解是因为增加了曲率约束，而曲率约束是非线性的，优化目标的设置同OSQP一致，只是增加了松弛因子。

1. 优化目标

1.1 平滑性

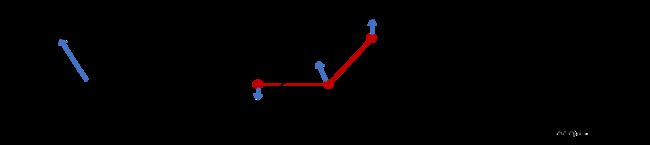
参考线平滑的首要目标当然是平滑性，使用向量的模$|P_2{P}_2^{\prime }|$来表示，显然$|P_2{P}_2^{\prime }|$越小，三个点$P_1,P_2,P_3$越接近一条直线，越平滑。
$$J_{smooth}=\sum _{i=2}^{N-1}|P_i{P}_i^{\prime }{|}^2=\sum _{i=2}^{N-1}|P_i{P}_{i-1}+P_i{P}_{i+1}{|}^2=\sum _{i=2}^{N-1}((x_{i-1}+x_{i+1}-2x_i{)}^2+(y_{i-1}+y_{i+1}-2y_i{)}^2)\text{\hspace{1em}(1-1)}$$

1.2 几何性

平滑后的参考线，希望能够保留原始道路的几何信息，不会把弯道的处的参考线平滑成一条直线。使用平滑后点与原始点的距离来表示。
$$J_{deviation}=\sum _{i=1}^N|P_{r,1}{P}_1{|}^2=\sum _{i=1}^N((x_1-x_{1,r}{)}^2+(y_1-y_{1,r}{)}^2)\text{\hspace{1em}(1-2)}$$

1.3 均匀性

平滑后的参考线的每两个相邻点之间的长度尽量均匀一直。
$$J_{length}=\sum _{i=1}^{N-1}|P_i{P}_{i+1}{|}^2=\sum _{i=1}^{N-1}((x_{i+1}-x_i{)}^2+(y_{i+1}-y_i{)}^2)\text{\hspace{1em}(1-3)}$$

因此，参考线平滑的优化目标可以定义为：
$$J=w_{smooth}\ast J_{smooth}+w_{deviation}\ast J_{deviation}+w_{length}\ast J_{length}\text{\hspace{1em}(1-4)}$$

2. 约束条件

2.1 边界约束

只考虑边界约束，即：
$$\begin{gathered} x_{i,lower}\le x_i\le x_{i,upper} \\ {y}_{i,lower}\le y_i\le y_{i,upper}\text{\hspace{1em}(2-1)} \end{gathered}$$
可以转化为：
$$\begin{gathered} x_{i,r}-bound\le x_i\le x_{i,r}+bound \\ {y}_{i,r}-bound\le y_i\le y_{i,r}+bound\text{\hspace{1em}(2-2)} \end{gathered}$$
对参考线的起点和终点进行约束，令其等于原始参考线上的点：
$$\begin{gathered} x_{1,r}\le x_1\le x_{1,r} \\ {y}_{1,r}\le y_1\le y_{1,r}\text{\hspace{1em}(2-3)} \end{gathered}$$

2.2 曲率约束

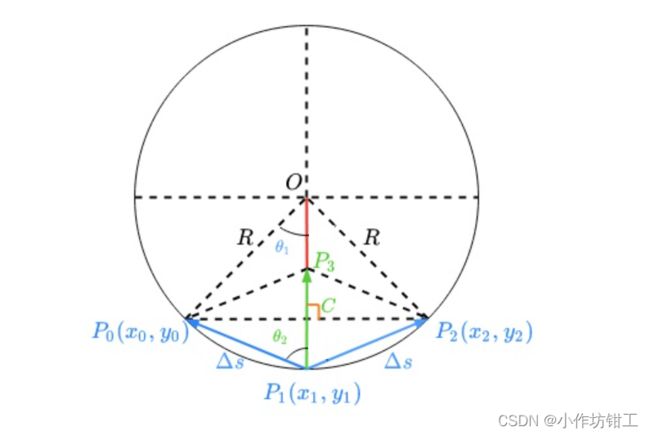
文章Apollo ReferenceLine Smooth–离散点平滑原理中详细叙述了曲率的计算过程。

$$\begin{gathered} |P_1{P}_3|=\Delta s^2\times \kappa \\ |P_1{P}_3|\le \Delta s^2\times {\kappa }_{max}\text{\hspace{1em}(2-4)} \end{gathered}$$
因此中间的$N-2$个点上的曲率应该满足约束：
$$(x_{i-1}+x_{i+1}-2x_i{)}^2+(y_{i-1}+y_{i+1}-2y_i{)}^2\le (\Delta s^2\times {\kappa }_{max}{)}^2,i=1,2,\cdots ,N-1\text{\hspace{1em}(2-5)}$$
为了保证有解，增加了松弛因子${\epsilon }_{\kappa }$：
$$\begin{gathered} (x_{i-1}+x_{i+1}-2x_i{)}^2+(y_{i-1}+y_{i+1}-2y_i{)}^2-{\epsilon }_{\kappa ,i}\le (\Delta s^2\times {\kappa }_{max}{)}^2,i=1,2,\cdots ,N-1 \\ {\epsilon }_{\kappa ,i}\ge 0,i=1,2,\cdots ,N-1\text{\hspace{1em}(2-6)} \end{gathered}$$

3. Ipopt

由于曲率约束是非线性的，因此可以使用Ipopt进行求解。在进行曲率约束时，需要使用$\Delta s$，Apollo使用了原始参考线两点之间的平均距离。

  // b. curvature constraints
  double ref_total_length = 0.0;
  auto pre_point = ref_points_.front();
  for (size_t i = 1; i < num_of_points_; ++i) {
    auto cur_point = ref_points_[i];
    double x_diff = cur_point.first - pre_point.first;
    double y_diff = cur_point.second - pre_point.second;
    ref_total_length += std::sqrt(x_diff * x_diff + y_diff * y_diff);
    pre_point = cur_point;
  }
  double average_delta_s =
      ref_total_length / static_cast(num_of_points_ - 1);
  double curvature_constr_upper =
      average_delta_s * average_delta_s * curvature_constraint_;

  for (size_t i = curvature_constr_start_index_;
       i < curvature_constr_end_index_; ++i) {
    g_l[i] = -1e20;
    g_u[i] = curvature_constr_upper * curvature_constr_upper;
  }

在Apollo中使用的ADOL-C自动求解优化目标的梯度向量函数、约束函数的雅可比矩阵和拉格朗日函数的黑森矩阵。可以参考文章Planning基础库——散点曲线平滑。