LeetCode - 743 网络延迟时间

目录

题目来源

题目描述

示例

提示

题目解析

算法源码

---

题目来源

743. 网络延迟时间 - 力扣（LeetCode）

题目描述

有 n 个网络节点，标记为 1 到 n。

给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。

现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

示例

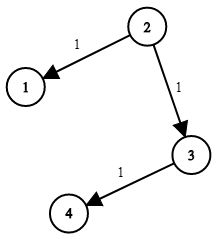
输入	times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出	2
说明	如上图

输入	times = [[1,2,1]], n = 2, k = 1
输出	1

输入	times = [[1,2,1]], n = 2, k = 2
输出	-1

提示

1 <= k <= n <= 100
1 <= times.length <= 6000
times[i].length == 3
1 <= ui, vi <= n
ui != vi
0 <= wi <= 100
所有 (ui, vi) 对都 互不相同（即，不含重复边）

题目解析

本题是典型的单源最短路径问题。

所谓“单源最短路径”，即图结构中，已某个点为源点，计算源点到另一个点之间的最短路径（即最小权重）。

要理解上面“单源最短路径”问题，我们需要有一些图结构的基础认识。

图结构由：顶点和边组成。比如下图中圆圈就是顶点，圆圈和圆圈之间的线就是边。

如果边是有方向的（即单向），则图称为有向图，

如果边是没有方向的（即双向），则图称为无向图。

边除了有方向性外，还有权重，所谓权重，可以简单理解为构成边的两个顶点之间的距离。如上图中顶点1和顶点2构成的边的权重就是1。

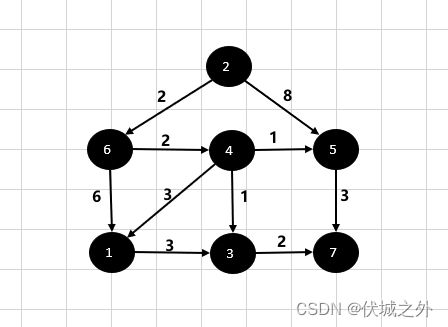
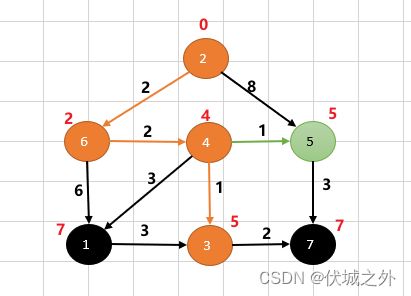
图中某个点想要到达另一个点可能存在多条路径，如下图从顶点2到达顶点7的路径有：

• 2 → 5 → 7 （权重11）
• 2 → 6 → 4 → 5 → 7（权重8）
• 2 → 6 → 4 → 3 → 7（权重7）
• 2 → 6 → 4 → 1 → 3 → 7（权重12）
• 2 → 6 → 1 → 3 → 7（权重13）

而其中路径权重最小的，即路径最短的只有一个，那就是2 → 6 → 4 → 3 → 7（权重7）

2 → 6 → 4 → 3 → 7就是要求的顶点2到顶点7的单源最短路径。

而本题是 “从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号”，即本题要求从K节点到剩余其他各店的单源最短路径，并返回这里最短路径中最大的那个。

在理解本题题意后，接下来我们考虑如何求解本题，而在求解本题前，我们必须要先将图结构通过代码模拟出来。

图结构的实现，有两种方式：

• 邻接矩阵
• 邻接表

比如上图用邻接矩阵模拟即为：

const x = Infinity;
const graph = [
    [0, x, x, x],
    [1, 0, 1, x],
    [x, x, 0, 1],
    [x, x, x, 0]
]

矩阵含义，若 graph[i][j] != Infinity，即表示 i+1顶点和j+1顶点相邻，且是i+1指向j+1，权重为graph[i][j]值。

上图如果用邻接表模拟即为：

const graph = {
    2: [[1,1], [3,1]]
    3: [[4,1]]
}

对象含义是graph对象的属性是起点，graph对象的属性值是一个数组，这是因为图中一个顶点可以和多个其他点相连，graph对象的属性值数组的元素还是数组，这是因为元素数组的第一个值是起点的邻接点，第二个值是起点到该邻接点的权重。

比如graph[2][1] = [3,1]，表示从顶点2出发，到邻接点3的权重是1。

对比来看，邻接表模拟图结构在内存消耗上代价更小，因此我们一般选择邻接表来模拟图结构。

接下来就是实现单源最短路径的求解算法了，这里其实可以使用图结构的两种遍历方法：

• 深度优先搜索，即dfs
• 广度优先搜索，即bfs

但是最短路径问题，一般不用dfs，因为深度优先搜索，需要将图结构中从源点出发的所有路径可能都找到，然后才能比较出最短路径，这种其实相当于暴力破解，性能非常低。

可能有人会有疑问，广度优先搜索不也相当于暴力吗？

的确，bfs和dfs其实都相当于暴力，但是bfs可以结合贪心算法思维，让最短路径的查找变为类似于二叉树的二分查找。

接下来我们通过图示来看看bfs结合贪心算法思维是如何实现图中单源最短路径的查找的：

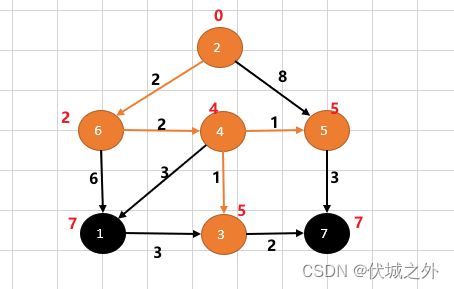
下面我们需要求解下图中，从源点2到其他各点的最短路径

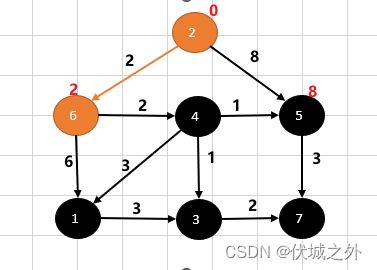
广度优先搜索，肯定是先搜索源点的直接临界点6和5。

我们假设源点2到自身的权重为0，则源点2到顶点6的权重为0+2，我们将其更小为顶点6的权重。

同理，我们将顶点5的权重更新为8。

这里顶点权重的含义是：从源点到达该顶点所需要花费的代价（即所经过边的权重累加之和）。

也就是说，从源点2触发，有两个选择，2→6和2→5，根据贪心算法思维，每个局部达到最优，则最终结果也会最优。

因此，我们选择权重更小的2→6。即我们认定从2出发，必然要选择6，可以理解为从2出发的第一条路径。

 接下来，我们将6当成出发点，则有两个选择，6→1和6→4 ，

此时顶点6的权重是2，而

• 6→1边权重为6，
• 6→4边权重为2，

因此从顶点6出发，到顶点4的代价更小，顶点4的权重为2+2。

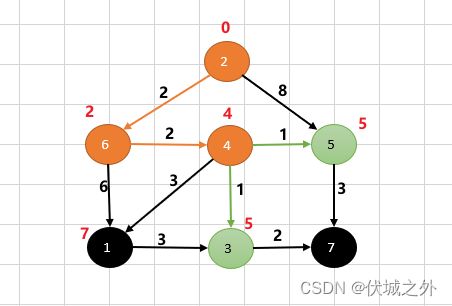
接下来，从顶点4出发，有三个选择：

• 4 → 1 
• 4 → 3
• 4 → 5 

其中4 → 1 ，即 2 → 6 → 4 → 1 会让顶点1的权重变为7，这要比 2 → 6 → 1赋给顶点1的权重8要小，因此我们将顶点1的权重更新为7。

4 → 3，即 2 → 6 → 4 → 3会让顶点3的权重变为5。

4 → 5 ，即2 → 6 → 4 → 5会让顶点5的权重变为5，这要比 2 → 5赋给顶点5的权重8要小，因此我们将顶点5的权重更新为5.

因此，上面3条路径，我们有两个等价选择，即4 → 3或4 → 5 ，它们的总权重相同，因此我们都要试一下。

 我们可以先选择4 → 3

此时从顶点3出发，只有一条路径，即3→7，因此顶点7的权重设为5+2=7

接下来选择4→5

此时从顶点5出发，只有一条路径，即5→7，而此时顶点7的权重为5+3=8，大于之前3→7的赋予的权重7，因此不更新

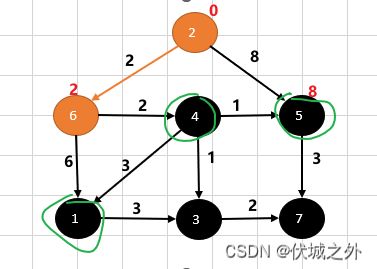
此时，从源点2到到其他所有点的权重（最短路径）已经被全部求解出来了，

• 2 → 1（权重7）
• 2 → 3（权重5）
• 2 → 4（权重4）
• 2 → 5（权重5）
• 2 → 6（权重2）
• 2 → 7（权重7）

而以上，结合了广度优先搜索和贪心思维的算法就是Dijkstra算法，即迪杰斯特拉算法。

Dijkstra算法是专门用于求解图结构中单源最短路径问题，但是Dijkstra算法要求图结构中的边的权重值不能有负数。

Dijkstra算法的实现有一定的技巧，除了模拟图结构（使用邻接表）外，还需要定义一个长度为n（n为图结构中顶点的个数）的数组dist

dist数组的

• 索引值被当成对应顶点
• 元素值被当成源点到对应顶点的权重累计和

我们最终会将源点到各个顶点的最小权重值统计出来并保存在dist中，然后从dist中取出最大的即可最小权重即为题解。

dist数组初始时，会将源点到各个顶点的权重值设为Infinity，这样可以方便初次更新dist[i]顶点权重时必然成功，因为一般情况下顶点权重值都小于Infinity。

另外，我们实现Dijkstra算法，我们还需要一个优先队列，那么什么是优先队列，它的作用是什么呢？

优先队列(priority queue)：普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。

在Dijkstra算法中，优先队列用于存放

 比如上图中，我们确定了 2 → 6 要比 2 → 5 的权重累计和更小，因此我们根据贪心思维局部最优原则，选择了 2 → 6，但是接下来我们不能只在下面两种路径种选择

• 2 → 6  → 1
• 2 → 6  → 3

因为无法确认上面两条路径的权重累计和一定比  2 → 5 的小，因此接下来的局部最优竞争中，有三个路径：

• 2 → 6  → 1
• 2 → 6  → 3
• 2 → 5

即比较1,3,5顶点此时的权重值，取最小的当成下一步

而优先队列的作用就是用于缓存有了这些有了权重值，但是不确定是否为最小权重的顶点。而这些顶点的权重越小，在优先队列中的优先级越高，也就越优先被出队。

而一旦顶点被从优先队列中出队，则可以认为已经确定该顶点的权重为最小权重。

当优先队列中没有顶点时，表示所有顶点的到源点的最小权重已经找到。

JavaScript中没有优先队列数据结构，但是我们可以使用数组来模拟，当我们向数组中加入一个新顶点时，就执行数组排序，排序规则是权重小的顶点在队头，权重达的顶点在队尾。

算法源码

var networkDelayTime = function (times, n, k) {
  // 邻接表
  const graph = {};

  // 初始化邻接表
  times.forEach((time) => {
    let [u, v, w] = time;
    graph[u] ? graph[u].push([v, w]) : (graph[u] = [[v, w]]);
  });

  // 源点k到其他点i的距离
  const dist = new Array(n + 1).fill(Infinity);

  // 源点到自己的距离为0，且是最短距离
  dist[k] = 0;

  let needCheck = []; // 优先队列
  while (true) {
    let flag = false // 是否执行优先队列的优先级排序
    graph[k]?.forEach((next) => {
      let [v, w] = next;
      let newDist = dist[k] + w;

      if (dist[v] > newDist) {
        dist[v] = newDist;
        if (needCheck.indexOf(v) === -1) { // 如果优先队列已有某顶点，则不再重复加入
            needCheck.push(v);
            flag = true
        }
      }
    });

    if (!needCheck.length) break;
    if (flag) needCheck.sort((a, b) => dist[a] - dist[b]); // 优先队列的优先级排序
    k = needCheck.shift();
  }

  dist.shift();
  let ans = Math.max(...dist);
  return ans === Infinity ? -1 : ans;
};