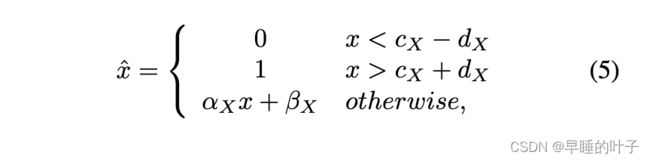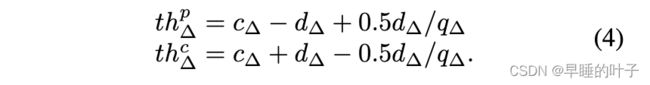Learning to Quantize Deep Networks by Optimizing Quantization Intervals with Task Loss 论文总结

论文精读

《Learning to Quantize Deep Networks by Optimizing Quantization Intervals With Task Loss》

• 参考：
  • 油管视频
  • 三星论文揭秘Exynos 9820 NPU核心技术，未来将应用于存储器和传感器
  • 论文地址
    

论文总览

三星的嵌入式AI轻量级算法，在CVPR （19年） 上引入了一篇题为 《Learning to Quantize Deep Networks by Optimizing Quantization Intervals With Task Loss》（可翻译为《通过优化量化间隔，借助任务损失学习量化深度神经网络》）的论文。嵌入式设备的AI能力可以直接计算和处理数据，最新的算法解决方案比现有算法轻4倍、速度快8倍，主要目是解决终端AI的低功耗和高性能问题。

三星高级技术研究院（SAIT）宣布他们已经成功开发了嵌入式（On-Device）AI轻量级技术,三星新的嵌入式AI处理技术通过“学习”确定影响深度学习整体成绩的重要数据的时间间隔。这种“量化间隔学习（QIL）1”通过重新组织，以小于其现有大小的比特位呈现的数据来保持数据准确性。SAIT进行的实验成功地证明了在计算到小于4位的水平时，32位间隔内的服务器深度学习算法的量化如何提供比现有其它解决方案更高的精度。

当深度学习计算的数据以低于4位的位组表示时，除了加法和乘法的算术计算之外，还允许进行’和’和’或’逻辑运算。这意味着使用QIL的计算可以获得与现有过程相同的结果，但只需要1/40至1/120甚至更少的晶体管。

由于该系统只需要较少的硬件和供电，可以将其直接安装在获得图像数据或指纹传感器中。

雷锋网当时报道，在NPU的支持下，Exynos9820相比Exynos99810人工智能性能提升7倍，并可以增强从照片到AR的性能。

• 量化的目的

  1. 减少功耗
  2. 加少内存占用
  3. 安全性

• 有哪些问题
  问题： 量化导致精度下降
  挑战： 降低量化导致的精度下降
  

• 相关工作

  通过一个可训练的量化器来学习量化激活和权重，从而转换和离散它们。具体地说，我们参数化量化区间，并通过直接最小化网络的任务损失得到其最优值。
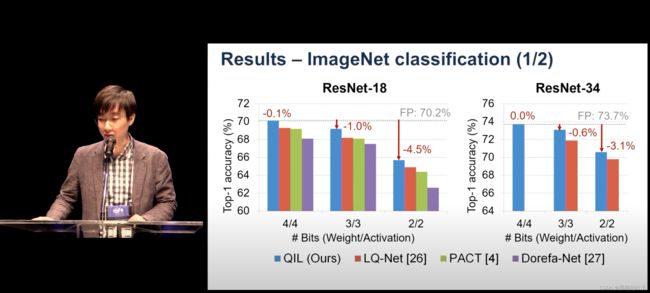
  在4bit能达到32bit的精度，在更低比特也能减小精度下降。
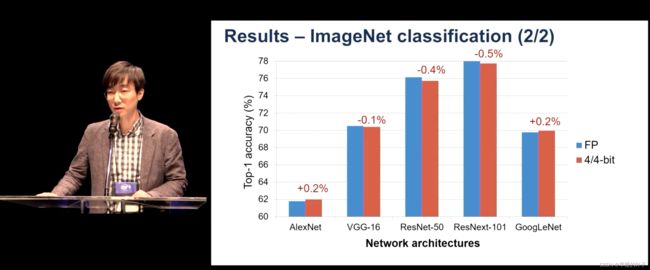
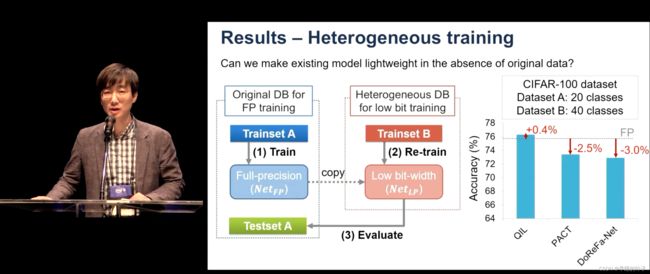
  此外，量化器可以在异构数据集上进行训练，因此可以用于量化预先训练过的网络，而无需访问它们的训练数据。用ResNet-18，-34和AlexNet，在iagenet上训练，达到了当时最先进的精度。

• 预处理‘
  
  量化器可以看作是Transformer和discretizer的组合。Transformer是一个（非线性）函数，从无界实值到标准化实值(即R（−∞，∞）→R[−1,1])，discretizer将归一化值映射到整数(即R[−1,1]→I)。在这里，我们建议将Transformer的量化间隔参数化，这允许我们的量化器通过剪枝（不那么重要）小值和剪切（很少出现）大值来集中于适当的量化间隔。

• 结果
  
  

  

• 总结
  

• QA
  

摘要

通过降低： 激活位宽 和 网络的权重， 来进行量化，但是这个步骤降低了精度。

本文通过一个可训练的量化器来量化激活和离散这个降低步骤。

量化器的职责是： 参数化量化区间（quantization intervals），通过最小化网络的任务损失来获得最优数值。 支持位宽到4位到 2-3位的精度退化，并且量化器可以在异构数据集上进行训练，所以可以用于量化预先训练过的网络，无需访问她们的数据集。

缩写QIL： 量化区间学习（quantization-interval-learning）

减少激活的位宽和深度网络的权重可以有效地计算并将它们存储在内存中，这对于将它们部署到资源有限的设备（例如手机）至关重要。然而，随着量化减少位宽通常会大大降低精度。为了解决这个问题，我们建议通过一个可训练的量化器来学习量化激活和权重，该量化器可以转换和离散化它们。具体来说，我们通过直接最小化网络的任务损失来参数化量化间隔并获得它们的最佳值。这种量化间隔学习（QIL）允许量化网络保持位宽低至 4 位的全精度（32 位）网络的准确性，并通过进一步降低位宽来最小化精度退化（即 3 位和 2 位）。此外，我们的量化器可以在异构数据集上进行训练，因此可用于量化预训练网络，而无需访问其训练数据。我们展示了我们的可训练量化器在具有各种网络架构（如 ResNet-18、-34 和 AlexNet）的 ImageNet 数据集上的有效性，在这些网络架构上，它优于现有方法以实现最先进的精度

1. 引言

目标： 旨在减少深度网络的权重和激活位宽，同时保持全精度网络的准确性
方法： 我们的可训练量化器既不逼近权重/激活值，也不逼近逐层卷积输出。相反，我们通过直接最小化网络的任务损失来量化每一层的权重和激活，这有助于它保持全精度对应物的准确性
**组成：**我们的量化器可以看作是一个 变压器（Transformer） 和一个 离散器（discretizer） 的组合。
Transformer是从无界实数值到归一化实数值的（非线性）函数（即 R(−∞,∞) → R[−1,1]），
离散化器将归一化值映射为整数（即，R[-1,1] → I)。

在这里，我们建议对转换器的量化间隔进行参数化，这允许我们的量化器通过修剪（不太重要）小值和修剪（很少出现）大值来专注于量化的适当间隔

请注意，我们的量化器适用于每一层的权重和激活。因此，**如果权重和激活的位宽变得足够低，则可以通过利用由逻辑运算（即“AND”或“XNOR”）和位计数[27]组成的按位运算来有效地计算卷积运算。**权重和激活量化器使用全精度权重联合训练。请注意，权重量化器和全精度权重仅在训练阶段保持和更新；在推理时，我们丢弃它们并仅使用量化权重

总而言之，我们的贡献有三个方面：

• 具有参数化区间的可训练量化器，它同时执行剪枝和剪切。
• 可训练量化器应用于深度网络的权值和激活，并以端到端方式对其进行优化和目标网络权值，以实现任务特定的损失。
• 实验表明，量化器在极低的位宽（2、3和4位）网络的ImageNet上达到了最先进的分类精度，并且即使在使用异构数据集进行训练和应用于预训练的网络时也能达到高性能。

2. 相关工作

低精度网络有两个好处：模型压缩和运算加速。一些工作通过减少模型权重的位宽来压缩网络

• BC（BinaryConnect）使用确定性或随机方法对 {−1, +1} 的权重进行二值化。
• BWN（Binary-Weight-Network） 将全精度权重近似为缩放双极 ({−1, +1}) 权重，并在封闭形式的解中找到尺度。
• TWN（Ternary-Weight-Network） 利用在训练阶段训练的具有缩放因子的三元（{−1, 0, +1}）权重。
• TTQ（Trained-Ternary-Quantizatio） 使用相同的量化方法，但在正反两面学习不同的缩放因子。
  这些方法仅考虑网络权重的量化，主要仅针对二元或三元情况，不考虑激活的量化

为了最大限度地利用逐位运算进行卷积， 我们应该对权重和激活进行量化。

• 二值化神经网络(BNN)以与BC相同的方式将权重和激活二值化为{−1，+1}，并使用这些二值化的值来计算梯度。
• XNOR-Net还使用标度因子进行激活二值化，其中标度因子是在闭合形式解中获得的。
• DoReFa-Net[27]通过使用多位量化权重和激活而不是执行双极量化来形成用于卷积的逐位运算。它们采用不同的激活函数来约束激活值。权值通过双曲正切函数进行变换，然后在量化前相对于最大值进行归一化。
• 半波-高斯-量化(HWGQ)[3]利用了激活的统计特性，提出了约束无界值的REU激活变量。
• DoReFa-Net和HWGQ都使用激活上限，但它们在训练过程中是固定的，并且它们的量化没有像我们的模型中那样被学习

一些工作[26，25，30，4]同时考虑了权重和激活量化，提出了高精度的低位宽模型。LQ网[26]允许浮点值表示K位量化值的基数而不是标准基数[1，2，…，2K−1]，并通过最小化量化误差来学习每一层或通道的权重和激活的基数。另一方面，我们的可训练量化器估计最优量化间隔，该间隔是根据最小化输出任务损失而不是最小化量化误差来学习的。此外，由于基于浮点运算，LQ-Net在计算卷积时必须使用少量的浮点乘法，但是我们的卷积可以使用移位运算而不是乘法，因为我们所有的量化值都是整数

Wang等人。[25]提出了一种分解激活和加权量化步骤的两步量化(TSQ)算法，在AlexNet和VG-GNET体系结构上取得了良好的性能。然而，TSQ采用LayerWise优化的加权量化步骤，因此不适用于包含跳跃连接的ResNet结构。相反，我们的量化器适用于任何类型的网络体系结构，而不受SKIP的限制/
庄某等人。[30]提出了一种两阶段渐进优化方法，以获得良好的初始化，避免网络陷入局部极小。我们采用了他们的渐进式策略，这实际上提高了精度，特别是对于极低位宽的网络，即2位。Pact[4]提出了一种参数化的剪裁激活函数，其中剪裁参数是在训练过程中获得的。然而，它没有考虑剪枝，并且像DoReFa-Net一样，权重量化是固定的。最近的一系列量化方法使用贝叶斯方法；Louizos等人。[18]提出了贝叶斯压缩，它通过估计的后验方差来确定每层的最佳比特精度数，但不计算权重。Achterhold等人。[1]提出了一种变分推理框架来学习量化良好的网络，该框架使用在量化目标值具有峰值的多模式量化先验。然而，这两种方法都不是修剪激活或学习量化器本身，就像我们在工作中所做的那样

论文中的量化器示意图：

3. 方法

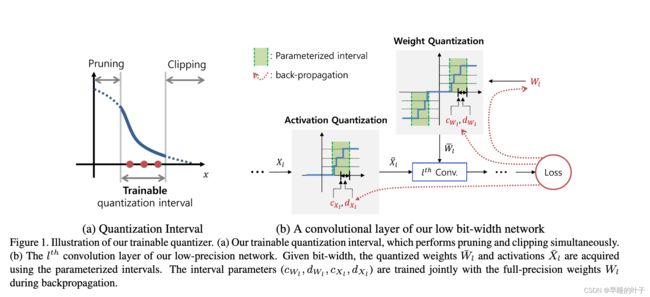
该可训练量化区间在该区间内具有量化范围，而修剪和剪辑范围在该区间之外。我们将可训练的量化间隔应用于激活和权重量化，并根据任务损失对它们进行优化。在这一部分中，我们首先回顾和解释了低位宽网络的量化过程，然后提出了具有量化间隔的可训练量化器。

分两步进行量化，每一步里都同时对权重和激活值进行处理。

权重：
激活：
We denote the elements of Wl and Xl by wl and xl,

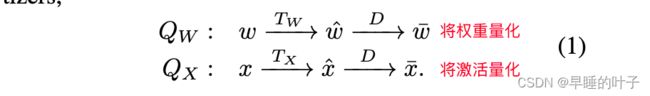
量化器Q∆(∆∈{W，X})由转换器（Transformer）T∆和离散器（discretizer）D组成。

• 转换器将权重和激活值映射到 [−1 ，1] 或 [0，1]。
  转换器最简单的例子是将这些值除以其最大绝对值的归一化。另一个例子是用于权重的tanh(·)和用于激活的夹击的函数[27]。
• 离散器将范围[−1，1] (或[0，1])中的实值ˆv映射到某个离散值̄v，如下所示
  

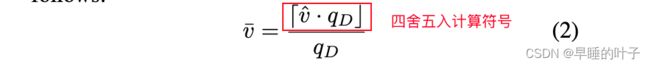
Transformer，思路与DoReFa-Net类似，将权重变换到[-1,1]，将激活值变换到[0,1]。

在本文中，我们对Transformer(变形器)进行参数化，使其可训练而不是固定。因此，量化器可以与神经网络模型权重一起进行联合优化。我们可以得到直接最小化整个网络的任务损失(即分类损失)的最优̄W和̄X(图1(B))，而不是简单地近似全精度权重/激活

最后的目标是：

可训练量化区间

为了设计量化器，我们考虑了两种操作：clipping和pruning(图1(A))。clipping的基本思想是限制量化的上限[27，4]。减小上界增加了上界内的量化分辨率，从而提高了低位宽网络的精度。另一方面，如果上限设置得太低，精度可能会降低，因为会裁剪太多的值。因此，设置适当的剪裁门限对于维持网络的性能至关重要。修剪删除了低值的权重参数[7]。增加剪枝阈值有助于提高量化分辨率和降低模型复杂度，而剪枝阈值设置过高会导致性能下降，原因与裁剪方案相同

我们定义了量化间隔来同时考虑剪枝和剪裁。为了自动估计区间，每一层的区间用c∆和d∆(∆∈{W，X})表示，其中c∆和d∆分别表示区间的中心和距中心的距离。请注意，这只是一种设计选择，其他类型的参数化也是可能的，例如具有下限和上限的参数化。

权重量化

让我们首先考虑权重量化。由于权重既包含正值也包含负值，因此量化器在正负两侧都具有对称性。给定区间参数CW和DW，我们将transformer（TW）定义如下

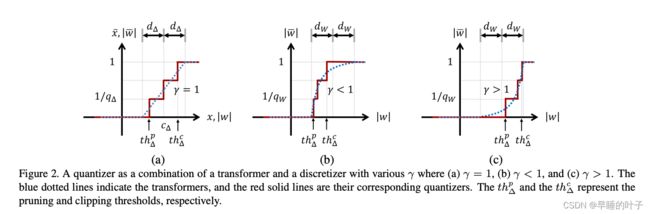
量化器由可训练的区间参数CW、DW和γ来设计。γ的非线性函数考虑区间内的分布。图2中的图表显示了具有不同γ的变压器(蓝色虚线)及其对应的量化器(红色实线)。如果γ=1，则变压器是分段线性函数，其中区间的内值被一致量化(图2(A))。通过调整γ(图2(b，c))，可以非均匀地量化内部值。γ可以被设置为固定值，也可以被训练。我们在实验中演示了γ的效果。如果γ6=1，则函数计算复杂。然而，在训练之后，权重量化器被重新移动，并且我们只使用量化的权重来进行推理。因此，这种复杂的非线性函数丝毫不降低推理速度。实际修剪阈值Thp∆和修剪阈值Thc∆根据参数Cw、Dw和∆而变化，如图2所示。例如，在∆=1的情况下，Thpγ和Thcγ被导出如下

一种量化器，由变压器和离散器组合而成，具有各种γ，其中(A)γ=1，(B)γ<1，©γ>1。蓝色虚线表示变压器，红色实线表示它们对应的量化器。ThP∆和THc∆分别表示修剪阈值和修剪阈值

激活量化

由于RELU操作，馈入卷积层的激活是非负的。对于激活量化，大于CX+DX的值被修剪并映射到1，而我们将小于CX的值−DX修剪为0。其间的值被线性映射到[0，1]，这意味着这些值在量化间隔内被均匀量化。与权值量化不同的是，在推理过程中需要在线进行激活量化，因此我们将γ固定为1以便于快速计算。然后，用于激活的变压器Tx定义如下(图2(A))