机器学习吴恩达课程学习笔记 Part1——从机器学习概念到线性回归
机器学习——吴恩达课程学习笔记 Part1
文章目录
- 机器学习——吴恩达课程学习笔记 Part1
-
- 一、**Introduction**
-
- **Welcome**
- 什么是机器学习
- 学习算法的类型:监督学习与无监督学习
-
- 监督学习 Supervised learning
- 无监督学习Unsupervised learning
- 二、线性回归
-
- 模型的表示
- 代价函数
-
- 代价函数的定义
- 代价函数的作用
- 梯度下降法
-
- 梯度下降的定义
- 线性回归的梯度下降
- 凸函数
- 批处理梯度下降法
- 三、多元线性回归
-
- 多元回归函数
- 多元梯度下降
-
- 多元梯度下降定义
- 梯度下降中的实用方法
-
- 特征缩放 feature scaling
- Debugging
- 四、特征和多项式回归
-
- 特征的选择
- 多项式回归
- 五、正规方程与向量化
-
- 正规方程的使用
- 使用选择
- 不可逆性
一、Introduction
Welcome
Machine Learning
- AI发展的一个工作
- 计算机的新能力
机器学习的例子:
- 数据挖掘:Web页面点击数据,医疗记录,生物,工程
- 机器编程(人无法手动编程):自然语言处理(NLP),计算机视觉
- 自我定制程序:推荐系统
- 理解人类
什么是机器学习
Arthur Samuel(1959):机器学习是一个给与机器学习的能力但不用显式编程的研究。
Tom Mitchell(1998):Well-posed Learning Problem: A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.
在跳棋游戏中类比E, P, T各是什么
学习算法的类型:监督学习与无监督学习
机器学习算法类型:
- 监督学习 Supervised learning
- 无监督学习 Unsupervised learning
其他名词:强化学习(Reinforcement learning),推荐系统(Recommender systems)……这是其他类型的机器学习算法,在之后视频中讲解。
学习工具->使用工具——学习机器学习算法->使用机器学习算法
监督学习 Supervised learning
监督学习:给算法数据集,并且给定正确答案。
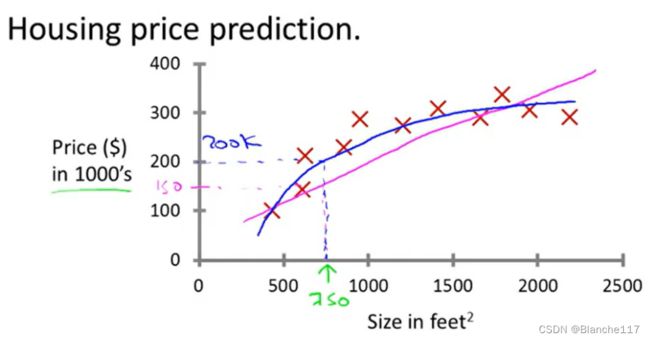
Example 1:房价预测例子
用更专业的术语来定义,称为回归问题。
之所以称为回归问题,是因为预测连续的输出值,也就是价格。
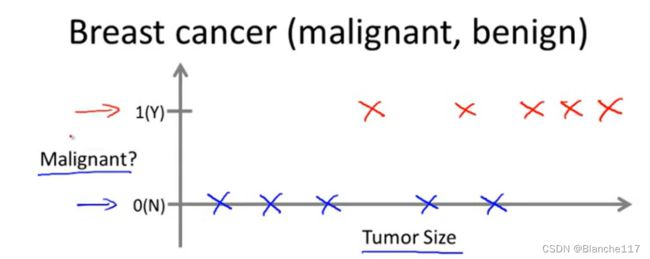
Example 2:癌症预测例子
专业术语来定义,属于分类问题。
分类指的是我们设法预测一个离散的输出值,比如这里的0或者1。在分类问题中,也可以有多余两个值。而特征的数量也可以不止这里的Tumor Size一个,可以有多个特征,如下:
一个更有趣的学习算法可以处理具有不仅1个特征,3个特征,5个特征,而是无穷个特征。
无穷个特征如何存储?不会溢出吗?
- 提出一个算法去解决它
无监督学习Unsupervised learning
对于无监督学习,我们不再知道数据的标签。
无监督学习会把这些数据分成两个不同的聚类,这被称为聚类算法。
注意与分类区别:聚类是无监督的学习,分类是有监督的学习

聚类算法的应用:
- 同类新闻聚类
- 组织大型计算机集群
- 社交网络分析
- 市场分割
- 天文数据分析
以上的这些例子都是聚类算法,实际上,聚类算法只是无监督学习的一种。
引例》
鸡尾酒聚会问题:实现人声的分离。

二、线性回归
模型的表示
符号:
| 符号 | 含义 |
|---|---|
| m | Number of training examples |
| x’s | “input” variable/features |
| y’s | “output” variable/“target” variable |
| (x,y) | one training example |
| ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i)) | i t h i^{th} ith training example |
训练集的定义:
-
学习算法的任务
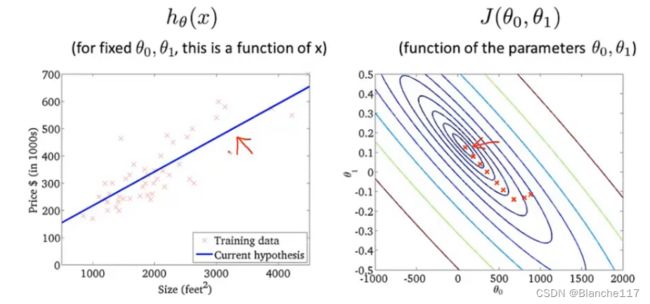
h h h为假设函数 ( h y p o t h e s i s ) (hypothesis) (hypothesis)是一个从 x x x到 y y y的函数
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IS7xEB25-1667739630954)(https://cdn.jsdelivr.net/gh/Holmes233666/blogImage@main/img/image-20221105144916815.png)]](http://img.e-com-net.com/image/info8/a154ae4b8d454b6d96bb0d14a8401ca6.jpg)
假设hypothesis为:
h θ ( x ) = θ 0 + θ 1 x h_{\theta}(x)=\theta_0+\theta_1 x hθ(x)=θ0+θ1x
代价函数
代价函数的定义
如何选择 h θ ( x ) h_\theta(x) hθ(x)中的 θ 0 \theta_0 θ0和 θ 1 \theta_1 θ1?我们的目标是:
min θ 0 , θ 1 1 2 m ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) 2 \min_{\theta_0,\theta_1}\frac{1}{2m}\sum_{i=1}^m(h(x^{(i)})-y^{(i)})^2 θ0,θ1min2m1i=1∑m(h(x(i))−y(i))2
其中 m m m是训练样本的个数。
定义代价函数:
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) 2 J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^m(h(x^{(i)})-y^{(i)})^2 J(θ0,θ1)=2m1i=1∑m(h(x(i))−y(i))2
目标:
m i n i m i z e θ 0 , θ 1 J ( θ 0 , θ 1 ) minimize_{\theta_0,\theta_1}J(\theta_0,\theta_1) minimizeθ0,θ1J(θ0,θ1)
代价函数有时也被称为平方误差函数,平方代价误差函数。平方代价误差函数对于大部分回归问题都是代价函数的一个合理选择。也有其他的代价函数,但是平方误差代价函数是解决回归问题最常见的代价函数。
代价函数的作用
在上述的假设函数上做进一步的简化: θ 0 = 0 \theta_0=0 θ0=0。
-
假设函数与代价函数的图像对比:
每个不同的 θ 1 \theta_1 θ1对应一个不同的假设函数,对应一个不同的代价函数的值 J ( θ 1 ) J(\theta_1) J(θ1)。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GatBUZIU-1667739630955)(https://cdn.jsdelivr.net/gh/Holmes233666/blogImage@main/img/image-20221105155929143.png)]](http://img.e-com-net.com/image/info8/d115820d4db7480798582ac63bef211e.jpg)
回到初始的 θ 0 ≠ 0 \theta_0\neq 0 θ0=0时的情况:
此时我们的代价函数也是碗状,但是是一个曲面:
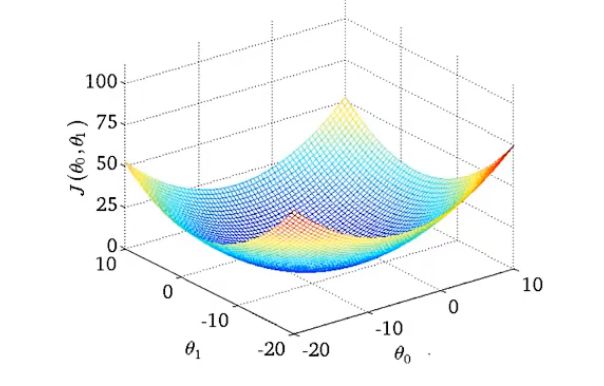
下面使用等高线图绘制:
梯度下降法
将代价函数 J ( θ ) J(\theta) J(θ)最小化的常用方法是梯度下降法。梯度下降法不仅用于线性回归,还用于机器学习的其他领域,最小化其他的函数,而不仅是回归函数。
使用梯度下降最小化任意函数 − > 应用在线性回归中 使用梯度下降最小化任意函数->应用在线性回归中 使用梯度下降最小化任意函数−>应用在线性回归中
问题描述:

首先初始化两个参数的值,通常来说,初始化为: θ 0 = 0 , θ 1 = 0 \theta_0=0,\theta_1=0 θ0=0,θ1=0。
在梯度下降中要做的就是不断一点点改变 θ 0 \theta_0 θ0和 θ 1 \theta_1 θ1,来使 J ( θ 0 , θ 1 ) J(\theta_0,\theta_1) J(θ0,θ1)最小,直到我们找到了最小值。
以下图为例,进行梯度下降:
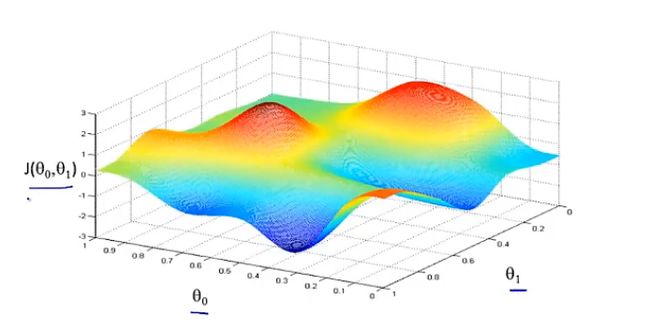
梯度下降的思想:在某个点时,如果希望尽快下降函数的值,那么应该朝哪个方向迈步?
![]()
假设我们从下图所示的另一个点开始梯度下降:
![]()
可以发现,从不同的起始点开始进行梯度下降,我们会得到不同的局部最优解,这也是梯度下降的一个特点。
梯度下降的定义
其中 α \alpha α为学习率,控制下降的步伐的大小。
对于上述梯度下降式子,我们需要同步更新 θ 0 , θ 1 \theta_0,\theta_1 θ0,θ1。同步意义如下:
![]()
-
从一个参数的 J ( θ ) J(\theta) J(θ)理解梯度下降的作用
θ : = θ − d d θ J ( θ ) \theta :=\theta-\frac{d}{d\theta}J(\theta) θ:=θ−dθdJ(θ)
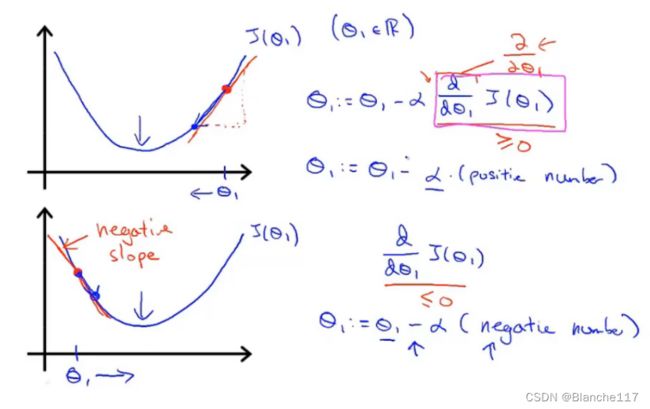
-
体会学习率的作用

- 学习率过小:收敛慢,逐步逼近最低点
- 学习率过大:收敛块,可能造成震荡,无法收敛甚至发散
-
已经处于最低点,那么下一步梯度下降会怎么样?
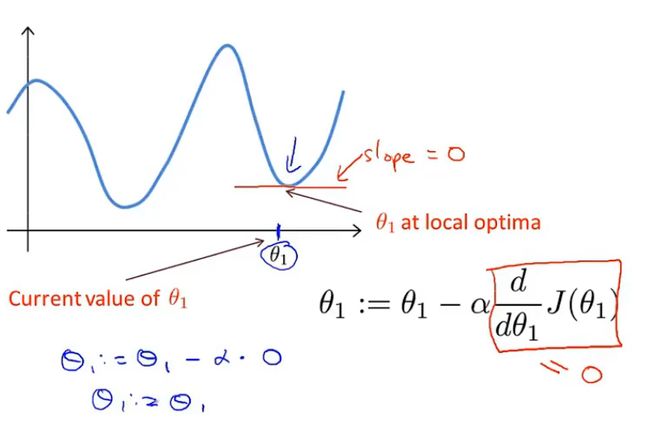
如果已经在最低点,那么导数会为0,梯度下降其实什么也没做。这也是我们想要的:使其保持在局部最优点。
-
即是 α \alpha α不变,梯度下降也会收敛到一个局部最小值
越接近最低点,导数的值越趋近于0,所以实际上没有必要去减少 α \alpha α的值

线性回归的梯度下降
将梯度下降与代价函数结合,得到线性回归的算法。
目的:将梯度下降应用在平方代价函数中,最小化代价。
将微分的结果代入线性回归模型,得到线性回归中梯度下降如下:
凸函数
线性回归的代价函数总是和这样的一个弓形函数相似,术语叫做“凸函数”(convex function),这样的函数没有局部最优解,只有全局最优解。
![]()
对这种函数使用梯度下降时,总能收敛到全局最优。
批处理梯度下降法
Batch Gradient Descent:意味着每一步梯度下降都遍历了整个训练集的样本。即在每一步梯度下降中,我们计算所有样本的误差总和。还有一些其他的梯度下降方法,他们没有遍历整个训练集的样本,每次只关注小的子集。
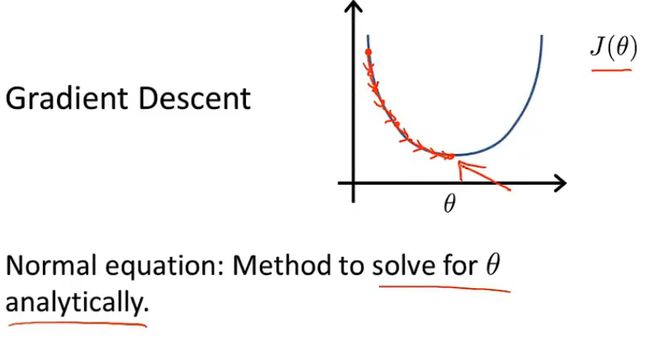
另外一种可以求出最优解的值,但是不用使用梯度下降的方法:正规方程组法。事实上梯度下降相比于正规方程组法,适用于更大的数据集。
三、多元线性回归
多元回归函数
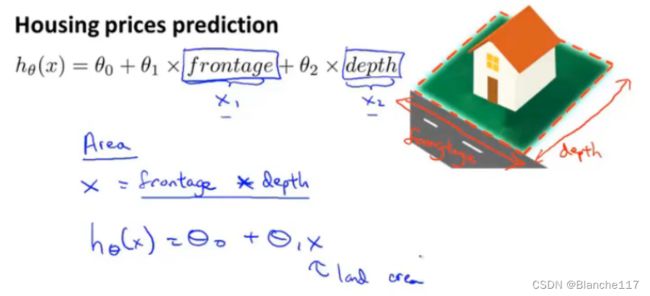
在上述房价的例子中,假如特征不止房子的面积,还有其他的属性(如下表),这样的回归为多元回归:
image-20221105215837697
符号:
| 符号 | 含义 |
|---|---|
| n | Number of features |
| x ( i ) x^{(i)} x(i) | input feature of i t h i^{th} ith training example |
| x ( i ) j x^{(i)_j} x(i)j | value of feature j in i t h i^{th} ith training example |
特征的增加,假设函数也会发生变化:
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n h_\theta(x)={\theta_0}+{\theta_1} x_1+{\theta_2 x_2}+\cdots+{\theta_n} x_n hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn
For convenience of notation, define x 0 = 1. ( x 0 ( i ) = 1 ) x_0=1 . \quad\left(x_0^{(i)}=1\right) x0=1.(x0(i)=1)
x = [ x 0 x 1 x 2 ⋮ x n ] ∈ R n + 1 θ = [ θ 0 θ 1 θ 2 ⋮ θ n ] ∈ R n + 1 h θ ( x ) = θ 0 x 0 + θ 1 x 1 + ⋯ + θ n x n = θ T x \begin{aligned} &x=\left[\begin{array}{l} x_0 \\ x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right] \in \mathbb{R}^{n+1} \quad \theta=\left[\begin{array}{c} \theta_0 \\ \theta_1 \\ \theta_2 \\ \vdots \\ \theta_n \end{array}\right] \in \mathbb{R}^{n+1} \\ &h_\theta(x)=\theta_0 x_0+\theta_1 x_1+\cdots+\theta_nx_n =\theta^Tx \end{aligned} x=⎣ ⎡x0x1x2⋮xn⎦ ⎤∈Rn+1θ=⎣ ⎡θ0θ1θ2⋮θn⎦ ⎤∈Rn+1hθ(x)=θ0x0+θ1x1+⋯+θnxn=θTx
称为多元线性回归(multivariate linear regression)。
多元梯度下降
如何使用梯度下降解决多元线性回归。
多元梯度下降定义
假设函数: h θ ( x ) = θ T x = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n h_\theta(x)=\theta^Tx=\theta_0x_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n hθ(x)=θTx=θ0x0+θ1x1+θ2x2+...+θnxn
参数: θ 0 , θ 1 , ⋯ , θ n \theta_0,\theta_1,\cdots,\theta_n θ0,θ1,⋯,θn
代价函数: J ( θ 0 , θ 1 , ⋯ , θ n ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_0,\theta_1,\cdots,\theta_n)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2 J(θ0,θ1,⋯,θn)=2m1∑i=1m(hθ(x(i))−y(i))2或者改写成其向量模式 J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2 J(θ)=2m1∑i=1m(hθ(x(i))−y(i))2
那么多元梯度下降算法为:
梯度下降中的实用方法
特征缩放 feature scaling
有一个机器学习模型,如果这些特征的取值都处在一个相近的范围,那么梯度下降法就能更快的收敛。如下图:
![]()
特征缩放时:
实用特征缩放能使梯度下降变得更快。
Debugging
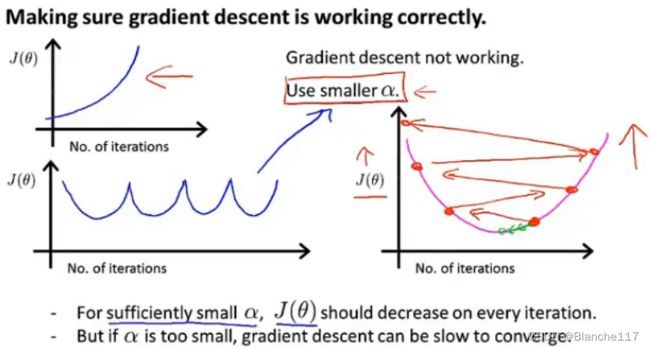
保证梯度下降是正常进行的:在进行梯度下降时,绘制出代价函数 J ( θ ) J(\theta) J(θ)与迭代次数的曲线。如果梯度下降是正常的,那么 J ( θ ) J(\theta) J(θ)应该随着迭代的进行值不断变小。
image-20221106145106094
同时,上图也可以帮助判断梯度下降何时会收敛。
有时也可以通过选择一个较小的阈值 ϵ \epsilon ϵ,当迭代后,减少小于这个阈值,那么认为梯度下降已经收敛。但是实际上,选择这样一个合适的 ϵ \epsilon ϵ是困难的。
-
学习率过大的情况
总结:
- 学习率过小:收敛缓慢
- 学习率过大: J ( θ ) J(\theta) J(θ)可能不会在每次迭代后收敛,甚至不会收敛
选择 α \alpha α:
……,0.001,……,0.01,……,0.1,……,1,……
![]()
四、特征和多项式回归
特征的选择
Example:房价预测的例子
多项式回归
下图所示的回归曲线,可以使用而次多项式,但是可以转而使用三次多项式。使用多项式,进行变量替换,就可以将线性回归的方法应用在多项式回归上。
![]()
需要注意的是,此时特征缩放就显得比较重要了。
另一种选择是使用平方根函数:
![]()
特征的选择是随意的,并且通过不同的特征选择可以使用更加复杂的函数去拟合数据,而不仅是一条直线去拟合,特别是可以使用多项式函数。有时从不同的角度去使用特征,能够得到一个更加符合数据的模型。
五、正规方程与向量化
正规方程的使用
正规方程:提供了一种求解 θ \theta θ的方法
使用正规方程不再需要进行迭代,而是一次性求出 θ \theta θ
Example:m=4
| size( f e e t 2 feet^2 feet2) | Number of bedrooms | Number of floors | Age of home (years) | Price($1000) | |
|---|---|---|---|---|---|
| x 0 x_0 x0 | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 | y y y |
| 1 | 2104 | 5 | 1 | 45 | 460 |
| 1 | 1416 | 3 | 2 | 40 | 232 |
| 1 | 1543 | 3 | 2 | 30 | 315 |
| 1 | 852 | 2 | 1 | 36 | 178 |
X = [ 1 2104 5 1 45 1 1416 3 2 40 1 1534 3 2 30 1 852 2 1 36 ] Y = [ 460 232 315 178 ] X=\left[\begin{array}{ccccc} 1 & 2104 & 5 & 1 & 45 \\ 1 & 1416 & 3 & 2 & 40 \\ 1 & 1534 & 3 & 2 & 30 \\ 1 & 852 & 2 & 1 & 36 \end{array}\right]\qquad Y=\left[\begin{array}{ccccc} 460 \\ 232\\ 315\\ 178 \end{array}\right] X=⎣ ⎡11112104141615348525332122145403036⎦ ⎤Y=⎣ ⎡460232315178⎦ ⎤
![]()
对于正规方程来说,不再需要特征缩放,但是对于梯度下降来说,特征缩放仍然很重要。
使用选择
梯度下降和正规方程各有各自的优缺点:
-
梯度下降
- 缺点
- 需要选择学习率 α \alpha α
- 需要迭代很多的次数
- 优点
- n很大时仍然可以求解得很好(此处n为特征的个数)
- 缺点
-
正规方程
-
缺点
-
当n很大时求解 ( X T X ) − 1 (X^TX)^{-1} (XTX)−1是一项很耗时的操作(矩阵求逆时间复杂度为 O ( n 3 ) O(n^3) O(n3))
什么时候n算大呢?
n=100,或者1000都是可以使用正规方程的,但是如果到了n=10000的量级,那么会开始考虑使用梯度下降。大于10^4量级时,使用梯度下降更优。
-
-
优点
- 不用选择学习率
- 不需要迭代
-
总结:对于线性回归,当特征的数量不大时,使用正规方程是一个计算 θ \theta θ的好的替代方法。
当进行类如logistics等分类时,正规方程的方法将不再适用,那时仍需要采用梯度下降的方法。
不可逆性
Normal Equation:
θ = ( X X T ) − 1 X T y \theta=(XX^T)^{-1}X^Ty θ=(XXT)−1XTy
当 X X T XX^T XXT不可逆时如何处理?
Octave:pinv(x'*x)*x'*y
pinv()函数为伪逆,inv()函数为逆。即前者当矩阵不可逆时也可以求出你想要的 θ \theta θ。(数学上可以证明)
通常情况下矩阵不可逆的原因:
-
训练的矩阵中有多余的特征
-
过多的特征( m ≤ n m\leq n m≤n)
比如10个样本,100个特征;通常面对这种情况,可以删除一些特征或者使用正则化regularization
![]()
向量化的处理保证了更新的同步性。