数据挖掘（三） 决策树

数据挖掘（三） 决策树

1.决策树 概述

决策树（Decision Tree）算法是一种基本的分类与回归方法，是最经常使用的数据挖掘算法之一。我们这章节只讨论用于分类的决策树。

决策树模型呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程。它可以认为是 if-then 规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。

决策树学习通常包括 3 个步骤: 特征选择、决策树的生成和决策树的修剪。

2.决策树 场景

一个叫做 “二十个问题” 的游戏，游戏的规则很简单: 参与游戏的一方在脑海中想某个事物，其他参与者向他提问，只允许提 20 个问题，问题的答案也只能用对或错回答。问问题的人通过推断分解，逐步缩小待猜测事物的范围，最后得到游戏的答案。

一个邮件分类系统，大致工作流程如下:

首先检测发送邮件域名地址。如果地址为 myEmployer.com, 则将其放在分类 "无聊时需要阅读的邮件"中。
如果邮件不是来自这个域名，则检测邮件内容里是否包含单词 "曲棍球" , 如果包含则将邮件归类到 "需要及时处理的朋友邮件", 
如果不包含则将邮件归类到 "无需阅读的垃圾邮件" 。

决策树的定义:

分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点（node）和有向边（directed edge）组成。结点有两种类型: 内部结点（internal node）和叶结点（leaf node）。内部结点表示一个特征或属性(features)，叶结点表示一个类(labels)。

用决策树对需要测试的实例进行分类: 从根节点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到其子结点；这时，每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配，直至达到叶结点。最后将实例分配到叶结点的类中。

3.决策树 原理

3.1 决策树 须知概念

信息熵 & 信息增益

熵（entropy）:
熵指的是体系的混乱的程度，在不同的学科中也有引申出的更为具体的定义，是各领域十分重要的参量。

信息论（information theory）中的熵（香农熵）:
是一种信息的度量方式，表示信息的混乱程度，也就是说: 信息越有序，信息熵越低。例如: 火柴有序放在火柴盒里，熵值很低，相反，熵值很高。

信息增益（information gain）:
在划分数据集前后信息发生的变化称为信息增益。

3.2 决策树 工作原理

如何构造一个决策树?

我们使用 createBranch() 方法，如下所示:

def createBranch():
'''
此处运用了迭代的思想。 感兴趣可以搜索 迭代 recursion， 甚至是 dynamic programing。
'''
    检测数据集中的所有数据的分类标签是否相同:
        If so return 类标签
        Else:
            寻找划分数据集的最好特征（划分之后信息熵最小，也就是信息增益最大的特征）
            划分数据集
            创建分支节点
                for 每个划分的子集
                    调用函数 createBranch （创建分支的函数）并增加返回结果到分支节点中
            return 分支节点

3.3 决策树 开发流程

收集数据: 可以使用任何方法。
准备数据: 树构造算法 (这里使用的是ID3算法，只适用于标称型数据，这就是为什么数值型数据必须离散化。 还有其他的树构造算法，比如CART)
分析数据: 可以使用任何方法，构造树完成之后，我们应该检查图形是否符合预期。
训练算法: 构造树的数据结构。
测试算法: 使用训练好的树计算错误率。
使用算法: 此步骤可以适用于任何监督学习任务，而使用决策树可以更好地理解数据的内在含义。

3.4 决策树 算法特点

优点: 计算复杂度不高，输出结果易于理解，数据有缺失也能跑，可以处理不相关特征。
缺点: 容易过拟合。
适用数据类型: 数值型和标称型。

4.实验

决策树判定是否买电脑

import pandas as pd

data=[['youth','high','no','fair','no'],
['youth','high','no','excellent','no'],
['middle_age','high','no','fair','yes'],
['senior','medium','no','fair','yes'],
['senior','low','yes','fair','yes'],
['senior','low','yes','excellent','no'],
['middle_age','low','yes','excellent','yes'],
['youth','medium','no','fair','no'],
['youth','low','yes','fair','yes'],
['senior','medium','yes','fair','yes'],
['youth','medium','yes','excellent','yes'],
['middle_age','medium','no','excellent','yes'],
['middle_age','high','yes','fair','yes'],
['senior','medium','no','excellent','no'],
]

data=pd.DataFrame(data,columns=['age','income','student','credit_rating','buy_computers'])

from sklearn.feature_extraction import DictVectorizer
from sklearn import preprocessing

# 对于文字型特征如何处理，这时就需要用LabelEncoder（标签编码）和One—Hot（独热编码）将其转换为相应的数字型特征，再进行相应的处理。
# Tree Model不太需要one-hot编码： 对于决策树来说，one-hot的本质是增加树的深度。
# 这里仍然使用ordinalencoder
enc = preprocessing.OrdinalEncoder()
enc.fit(data)
x=enc.transform(data)

X_train=x[:,0:4]
y_train=x[:,4]

from sklearn.tree import DecisionTreeClassifier

# 创建决策时分类器--ID3算法
tree_model=DecisionTreeClassifier(criterion="entropy")
# 可以使用"gini"或者"entropy"，前者代表基尼系数，后者代表信息增益。

# 喂入数据
tree_model.fit(X_train,y_train)

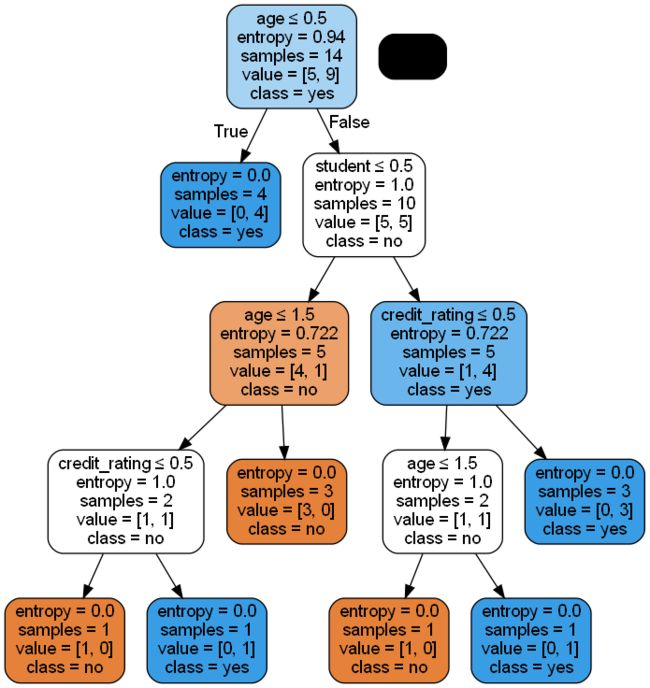
可视化：

# 可视化
from IPython.display import Image  
from sklearn import tree
import pydotplus 
 
 
dot_data = tree.export_graphviz(tree_model, out_file=None, 
                        feature_names=['age','income','student','credit_rating'],
                        class_names=['no','yes'],  
                        filled=True, rounded=True,  
                        special_characters=True)  
graph = pydotplus.graph_from_dot_data(dot_data)  
Image(graph.create_png())