CS224W摘要03.Node Embedding

CS224W: Machine Learning with Graphs
公式输入请参考： 在线Latex公式
上一节讲的是传统的图机器学习如何进行特征工程的（node-level, edge-level, graph-level features）
而这节课的目标是自动学习节点表征。

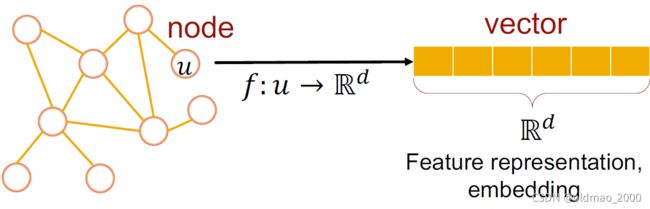
Encoder 和Decoder框架

基本的notation很简单：
V是节点集合，A是邻接矩阵，这里不为节点进行特征工程，或者添加额外信息。

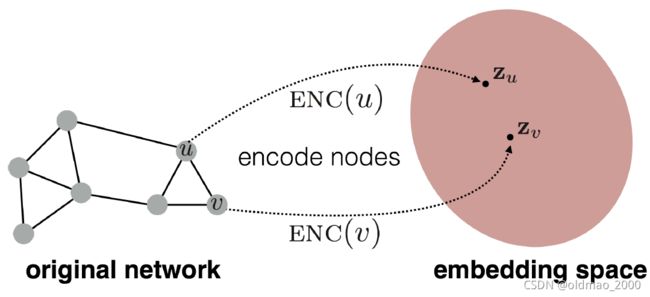
Goal is to encode nodes so that similarity in the embedding space (e.g., dot product) approximates similarity in the graph.
上图显示了Encoder，Decoder就是相似度计算部分：
$$DEC(z_v^T{z}_u)$$

Encoder小例子

这里使用最简单的线性变换作为encoding方法为例子：
$$ENC(v)=z_v=Z\cdot v$$
Z就是参数矩阵维度是$d\times |V|$；
$v$是节点的独热编码。
当然还有别的方法：DeepWalk, node2vec

Note

This is unsupervised/self-supervised way of learning node embeddings.
These embeddings are task independent. They are not trained for a specific task but can be
used for any task.

随机游走

notation

目标是要找到节点$u$对应的表征$z_u$
$P(v|z_u)$从节点$u$游走到节点$v$的概率
$z_u^T{z}_v$表示u和v同时出现在随机游走序列的概率

特点

1.即可获得邻居的local信息，也可以获取多跳邻居信息
Idea: if random walk starting from node visits with high probability, and are similar (high-order multi-hop information)
2.无需考虑节点对的采样，只用考虑随机游走策略$R$，更加高效
Efficiency: Do not need to consider all node pairs when training; only need to consider pairs that co-occur on random walks.

算法描述

给定图$G=(V,E)$
目标是学习到一种映射$f:u\to {\mathbb{R}}^d$，记为$f(u)=z_u$
目标最大化对数似然函数为：
$$\underset{f}{\max }\sum _{u\in V}\log P(N_R(u)|z_u)$$
$N_R(u)$表示用随机游走策略$R$对节点u进行遍历得到的邻居节点
我们希望学习到节点u的特征表达，特征表达可以预测其随机游走的邻居
上面的最大化对数似然函数可以写成：
$$\mathcal{L}=\sum _{u\in V}\sum _{v\in N_R(u)}-\log (P(v|z_u))$$
上面加了负号求最小，其中$P(v|z_u)$可以用softmax来求：
$$P(v|z_u)=\frac{\exp (z_u^T{z}_v)}{{\sum }_{n\in V}\exp (z_u^T{z}_n)}$$

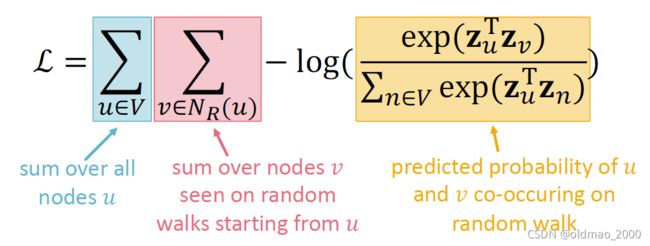
Optimizing random walk embeddings = Finding embeddings $z_u$ that minimize $\mathcal{L}$
直接算计算量很大，${\sum }_{u\in V},{\sum }_{n\in V}$两部分都是对所有节点进行操作，使得复杂度高达$O(|V{|}^2)$

负采样优化

这里主要针对黄色部分的进行优化，使得对所有节点的操作变成对某几个节点操作(k个采样的负样本)：
$$\log \frac{\exp (z_u^T{z}_v)}{{\sum }_{n\in V}\exp (z_u^T{z}_n)}\approx \log \left(\sigma (z_u^T{z}_v)\right)-\sum _{i=1}^k\log \left(\sigma (z_u^T{z}_{ni})\right),n_i\sim P_V$$
负样本的采样不是随机的，而是根据节点的度作为采样概率的依据进行采样。度越大，被采样的概率越大。通常采样的负样本个数为：$k=5\sim 20$

SGD

不解释，太多教程了

小结

1.Run short fixed-length random walks starting from each node on the graph
2. For each node collect $N_R(u)$, the multiset of nodes visited on random walks starting from
3. Optimize embeddings using Stochastic Gradient Descent:

Node2Vec

对随机游走策略进行优化，定义了二阶有偏随机游走的方式来生成$N_R(u)$
就是使用广度优先或胜读优先来进行随机游走，以获得不同的邻居信息。
BFS: Micro-view of neighbourhood

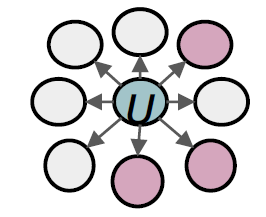
DFS: Macro-view of neighbourhood

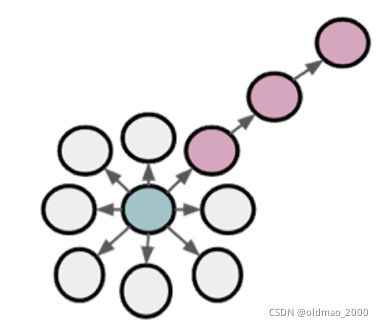
算法用到两个参数：
Return parameter : 用来控制是否Return back to the previous node
In-out parameter : 用来控制采用BFS vs. DFS来移动
具体看论文带读https://blog.csdn.net/oldmao_2001/article/details/108307211
从$s_1$出发后，当前游走到了$w$

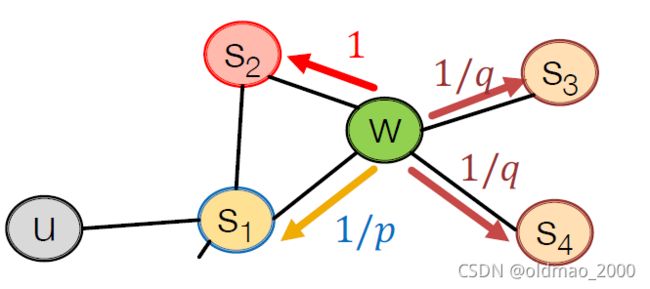
接下来该怎么走？

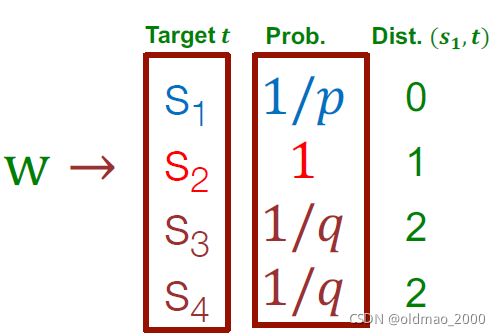
这里注意转移概率是非归一化的。

小结

Different notions of node similarity（Decoder做的事情）:
Naïve: similar if 2 nodes are connected
Neighborhood overlap (上节)
Random walk approaches (本节)

Embedding entire graphs

目标是找到子图或者整个图的表征：$Z_G$
常见任务：

1. 对有毒或无毒分子结构进行分类
2. 检测异常图结构

法1:用所有节点的表征来计算整个图的表征：
$$Z_G=\sum _{v\in G}{Z}_v$$

法2：使用虚拟的全局节点，然后用哪个该节点的表征作为图的表征

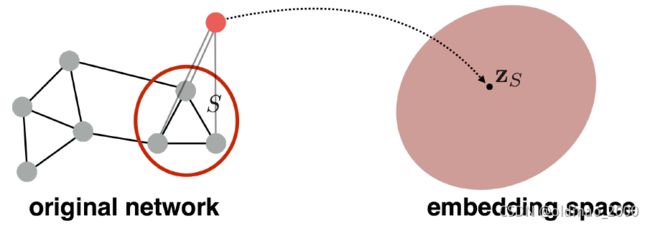
法3：使用anonymous walks表征，用游走序列中访问节点的顺序作为节点的index，然后得到index的序列作为图的表征。例如有图结构为：

下面两种随机游走结果对应的index序列一样：


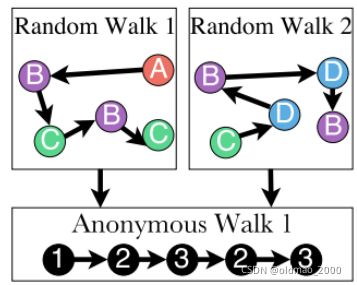
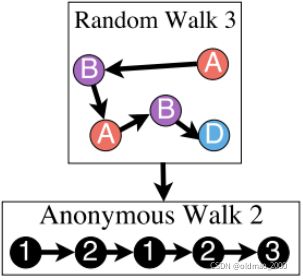
随着index序列的长度，节点组合也指数级增加：

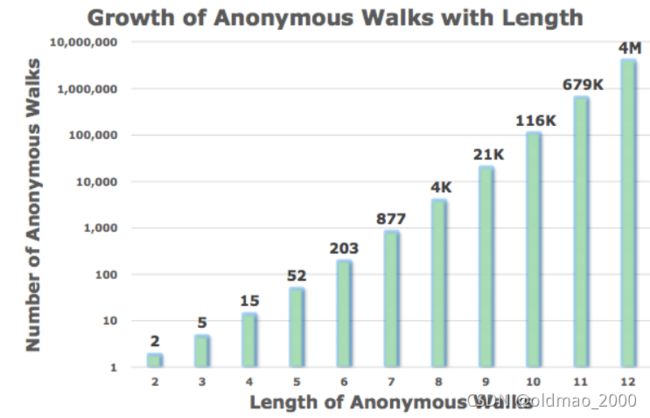
There are 5 anon. walks $w_i$ of length 3:
$w_1=111,w_2=112,w_3=121,w_4=122,w_5=123$
注意不会有133
有了anonymous walks结果后，用anonymous walks的概率分布来表征整个图。

例如：对于index长度为3的anonymous walks，我们知道可以表示一个5维向量
然后计算anonymous walks出现在$w_1=111,w_2=112,w_3=121,w_4=122,w_5=123$的次数即可。
采样anonymous walks的次数和我们想要得到的分布的概率参数有关，不展开，有公式。

新法 Learn Walk Embedding

这里是把anonymous walks的结果进行随机采样，然后得到一组anonymous walks的序列，例如图：

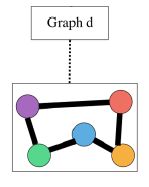
得到序列：

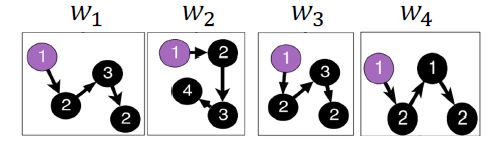
然后利用Node2Vec的思想，根据周围预测中间，然后训练得到图的表征，如果我们取窗口大小$\Delta =1$，那么就是要用$w_1,w_3$预测$w_2$