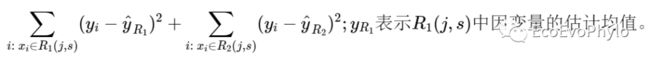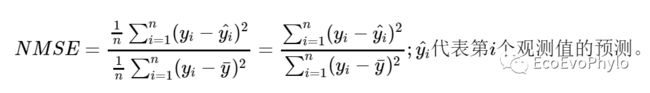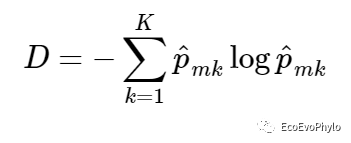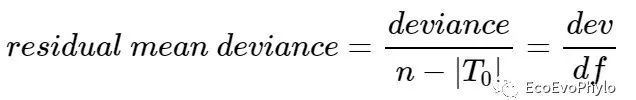机器学习-多元分类/回归决策树模型(tree包)

决策树(Decision Tree)：Tree-Based方法用于多元数据的分类和回归。决策树点是再现了人类做决策的过程，树可以图形化显示，很容易解释。但是树的分类和回归准确度比不上其他分类和绘图模型。决策树是随机森林、boosting等组合方法的基本组件，组合大量的树通常会显著提高模型的预测准确度，但会损失一些解释性。定性与定量变量均可用于Tree-Based方法。tree\rpart\mvpart均可进行多元树分析及绘图。此文介绍如何使用tree包进行多元分类/回归决策树分析。

 一、 准备数据

虚构微生物组和环境因子数据，包含75个样本。

# 1.1 导入数据
## 微生物组数据
spe = read.csv("spe.csv",row.names = 1,header = TRUE,check.names = TRUE,stringsAsFactors = TRUE) 
dim(spe)
head(spe)
​
## 环境因子数据
env = read.csv("env.csv",row.names = 1,header = TRUE,check.names = TRUE,stringsAsFactors = TRUE) 
dim(env)
head(env)

图1|原始otu表，spe.csv。前两列为分类信息。

图2|环境因子数据，env.csv。

二、决策树回归模型

当因变量为定量变量时，决策树进行回归分析。分析时先基于自变量划分预测空间Rj，此时残差平方和(residual sum of squares,RSS)值最小,然后对于落入某一预测空间的样本，做相同的预测。

但是考虑到所有自变量的预测空间构建基本很难实现，因此常使用递归二进制拆分(recursive binary splitting)。每一步的拆分都使RSS减少量最大。

如拆分点(cutpoint)为s，则拆分空间R1和R2为：

j和s的选择基于使RSS最小化：

后面重复此过程，寻找最佳预测空间和拆分点，从而使每个结果区域的RSS值最小，直到达到终止拆分标准，比如每个终端节点包含的样本数都不高于设定的阈值。

2.1 构建回归决策树

使用微生物数据与环境因子数据进行决策树回归分析。为了更好的评估分类树的分类性能，不能只计算训练误差，需要估计测试误差。将数据分为训练集和测试集数据，训练集数据用于构建模型，测试集数据用于模型评估。

# 2.1.1 将数据集分为train和test集，用train结果预测test的因变量值。
library(splitstackshape)
spe = data.frame(ID = rownames(spe),spe)# stratified提取后，样本名会消失,先提取样本名，重新构建数据框。
​
## train data sets，每个分类提取相同数目的样本用作训练集
set.seed(12345)
train.spe = stratified(spe, group=c("grazing"),size=10,replace=FALSE)
table(train.spe$grazing) # 每个分类提取的样本数一致。
​
train.env = env[rownames(env) %in% train.spe$ID,]
table(train.env$grazing) # 每个分类提取的样本数一致。
​
## test data sets
test.spe = spe[!spe$ID %in% train.spe$ID,]
table(test.spe$grazing)
​
test.env = env[!rownames(env) %in% rownames(train.env),]
table(test.env$grazing)

#install.packages("tree")
library(tree)
​
# 2.1.2 构建回归决策树
reg.tre = tree::tree(train.env$env1 ~.,data=train.spe[,-c(1:3)])
reg.tre
​
# 2.1.3 输出结果简介
## 输出表格的行为节点名(整数值表示)，包含9列数据。
reg.tre$frame 
## 列包括var：用于拆分节点的变量及终端节点();
reg.tre$frame$var
## n：每个节点的样本数量；
reg.tre$frame$n
## dev：每个节点的偏差
reg.tre$frame$dev
## yval:拟合结果，回归树为节点包含样本的因变量均值，分类树为该节点样本最多属于的分类水平；
#mean(train.env[reg.tre$where == 4,3]) # 第四个节点包含样本的因变量均值。
reg.tre$frame$yval
​
## split: 节点拆分，2列分别是属于左侧或右侧的标签；
reg.tre$frame$splits
## yprob：回归树，此为NULL；分类树则为因变量各水平的拟合比率，此数据有5个处理，所以有5列。
reg.tre$frame$yprob
​
## output，需要输出行名，则设置row.names=TRUE。
write.table(reg.tre$frame,"reg_tre_res.txt",sep="\t",quote = FALSE,row.names = FALSE)
​
## 每个样本所属节点
reg.tre$where
## formul形式
reg.tre$terms 
## 自变量数据，x=FALSE则不会返回此数据
reg.tre$x
## 因变量，y=FALSE则不会返回此数据
reg.tre$y
## 样本权重，未设置则均为1，权重值可以为分数形式。
reg.tre$weights
​
## 结果描述统计
reg.tre.res = summary(reg.tre)
reg.tre.res
reg.tre.res$used # 用于构建回归决策树的自变量
reg.tre.res$dev # 偏差，决策树的残差平方和。
reg.tre.res$df # 训练样本数减去终端节点数
reg.tre.res$residuals# 每个训练样本因变量的残差
​
##  简单绘图
plot(reg.tre)
text(reg.tre,pretty = 0)
​
# 2.1.4 预测测试集数据
reg.pred = predict(reg.tre,newdata = test.spe[,-c(1:3)])
reg.pred 
## 预测结果与原始结果绘图
plot(reg.pred,test.env$env1)
abline(0,1)
​
## 计算残差平方和(MSE)和标准化均方误差(NMSE)
MSE0 = mean((reg.pred-test.env$env1)^2)
MSE0
NMSE0 = mean((test.env$env1-reg.pred)^2)/mean((test.env$env1-mean(test.env$env1))^2)
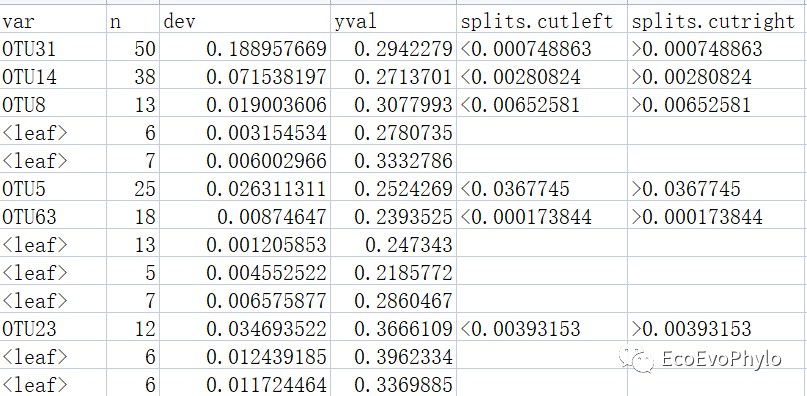
NMSE0

图3|回归树构建结果，reg.tre。每个节点以整数标注，tree()默认树最大生长数值为31。因子变量的分类水平不能超过32。

图4|回归树输出结果，reg_tre_res.txt。var：用于拆分节点的变量及终端节点()；n：每个节点的样本数量；dev：每个节点的偏差；yval:拟合结果，回归树为节点包含样本的因变量均值，分类树为该节点样本最多属于的分类水平；split: 节点拆分，2列分别是属于左侧或右侧的标签。

图5|回归树输出结果描述统计，reg.tre.res。包括终端节点数、拆分使用变量和残差平方和均值等信息。

图6|简单回归树绘图。回归决策树的每个节点上的数值是该节点处因变量的均值。

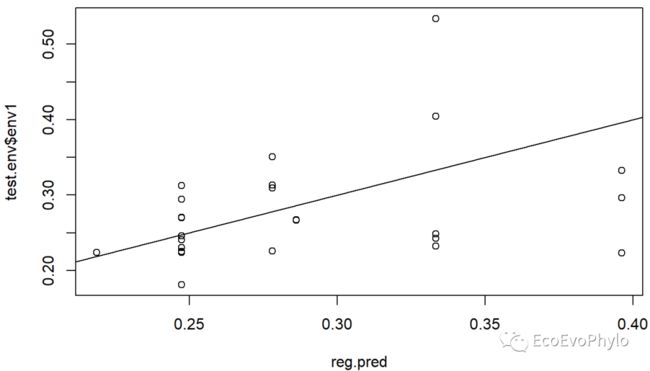
图7|测试数据因变量实际值与模型预测值散点图并添加趋势线。

图8|均方误差与标准化均方误差。评价模型预测好坏的一个准则为标准化均方误差(normalized mean squares error,NMSE)。

分母表示用最简单的算术平均来预测y的残差平方和。分子为该模型拟合后的残差平方和。此模型的NMSE不小于1，说明此回归模型没有任何意义(NMSE≥1)。此处是虚构数据，只讲使用方法，产生的模型没有任何意义，也没有影响。

2.2 优化模型-剪枝(Tree Pruning)

经过上述过程，构建的模型可能会过拟合，导致模型对训练集数据有很好的预测能力，但对测试集数据的预测能力较差。可能的原因是生成的决策树模型过于复杂。

解决的方法之一是仅在拆分能使RSS降低值超过某个阈值的情况下才继续进行拆分。但是低于某个阈值的拆分点的之后的拆分点可能降低RSS的能力很强，所以不能随意剪枝。所以更好的优化模型的方式是先不设定RSS阈值，构建一个较大的决策树T0,然后根据某种方法对其进行剪枝获得子树。

剪枝的标准主要为获得的子树的错误率最低，常用交叉验证选择具有最低错误率的子树。但是子树集一般很大，所以一般限定在一个更小的子树集中进行交叉验证。这里引入一个新的概念复杂性代价剪枝(Cost complexity pruning,或最弱链接剪枝(weakest link pruning))。此时剪枝不考虑每棵子树，而只考虑由非负调整参数α索引的树序列。然后基于交叉验证选择α。α控制着树的复杂性及树与训练数据的适配性之间的权衡，当α=0时，子树T就是T0;当α的值逐渐增大时，表示拥有许多终端节点的树要付出的复杂性代价，因此终端节点越少，α值将会越小。

这里介绍两个定义方差(variance)与偏差(bias):1)方差是训练数据集的预测值或预测分类水平相对于其他数据集的预测值或预测分类水平的离散程度，代表了模型的泛化能力。2)偏差是模型的预测值或预测分类水平与训练数据中的实际值或实际分类水平之间的差别，代表了模型的预测准确性。模型构建要在方差与偏差之间权衡，使总体误差(偏差+方差)最小。

一般模型越复杂，偏差越低，方差越高；简单模型一般偏差较高，方差较低，所以构建总误差较低的模型需要找到合适的模型复杂度。

# 2.2.1 交叉验证寻找最佳终端节点数
set.seed(12345)
reg.cv = cv.tree(reg.tre,K=10)
reg.cv
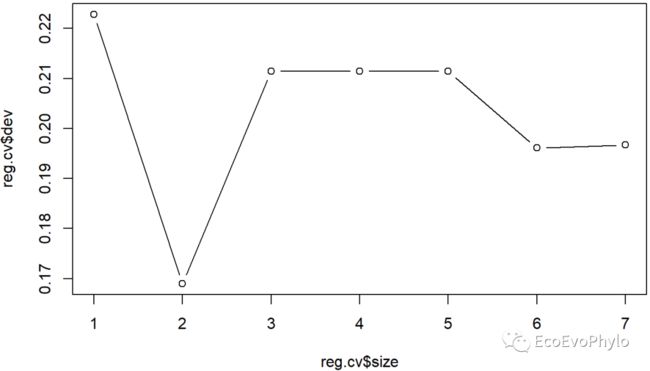
plot(reg.cv$size,reg.cv$dev,type="b") # 终端节点为2是偏差最小
​
# 2.2.2 剪枝优化模型
reg.prune.tre = prune.tree(reg.tre,best=2)
reg.prune.tre
​
# 2.2.3 绘图
plot(reg.prune.tre)
text(reg.prune.tre,pretty=0)
​
# 2.2.4 修剪树预测测试数据
reg.prune.pred = predict(reg.prune.tre,newdata = test.spe[,-c(1:3)])
reg.prune.pred 
## 预测结果与原始结果绘图
plot(reg.prune.pred,test.env$env1)
abline(0,1)
​
## 计算均方误差(MSE)和标准化均方误差(NMSE)
MSE1 = mean((reg.prune.pred-test.env$env1)^2)
MSE1 
NMSE1 = mean((test.env$env1-reg.prune.pred)^2)/mean((test.env$env1-mean(test.env$env1))^2)
NMSE1

图9|交叉验证结果，reg.cv。当终端节点为2时，交叉验证偏差值最小。

图10|交叉验证结果-终端节点数与对应偏差绘图。

图11|剪枝后预测结果的MSE与NMSE值。剪枝后模型的NMSE值仍然大于1，而且值反而增大了，因为原始模型就没有什么意义，剪枝对原本就没有意义的模型，达不到优化效果。

三、决策树分类模型 

分类决策树的因变量是定性变量，构建的模型也是用于对观测值进行分类预测。模型对变量进行递归二进制分裂来使树生长。分类误差(classification error rate)对树生长不够敏感，因此常用Gini index和cross-entropy两个指数对分类决策树模型准确率进行判断。

Gini index是节点纯度(purity)的检测值，其值较小，表示节点包含的样本更多属于单个分类。

3.1 tree包用于构建分类决策树(Classification Trees)

利用微生物组数据，以grazing为因变量，其它变量为自变量，构建决策树。

# 3.1.1 分类决策树
tre = tree::tree(grazing~.,train.spe[,-1],# 用于构建决策树的变量可以是分类变量或者定量变量。
                     na.action = na.omit,
                     split = "gini",# "deviance", "gini"
                     x=TRUE,
                     y=TRUE,
                     #wts = TRUE # 设置了样本weights参数，则返回权重值。
                       ) 
tre
## output
write.table(tre$frame,"class_tre_res.txt",sep="\t",quote = FALSE,row.names = FALSE)
​
# 3.1.2 描述统计
tre.res = summary(tre) # 输出用于中间节点拆分的变量，终端节点数目和error rate。
tre.res
tre.res$call
tre.res$type
tre.res$used # 用于中间节点拆分的变量
tre.res$size # 节点数目
df = tre.res$df # 自由度=样本数-终端节点数目
df
dev = tre.res$dev # 所有节点包含的分类偏差
dev
tre.res$misclass # 错误分类样本与总样本数目
​

图12|分类树输出结果，class_tre_res.txt。var：用于拆分节点的变量及终端节点()；n：每个节点的样本数量；dev：每个节点的偏差；yval:拟合结果，回归树为节点包含样本的因变量均值，分类树为该节点样本最多属于的分类水平；split: 节点拆分，2列分别是属于左侧或右侧的标签。yprob：回归树，此为NULL；分类树则为因变量各水平的拟合比率(即每个节点中属于各分类水平的样本的比例)，此数据有5个处理，所以有5列。

图13|分类树输出结果描述统计，tre.res。包含用于中间节点拆分的变量，终端节点数目和分类错误率等信息。

# 3.1.3  绘图查看决策树
plot(tre)
text(tre,pretty = 0)
​
# 3.1.4 预测测试数据集。
library(caret)
tre.pred0 = predict(tre,test.spe[,-c(1,2)],type = "class")  
## 生成混淆矩阵
caret::confusionMatrix(tre.pred0,test.spe[,2]) # 分类准确率为40%。
​

初次构建的决策树分类错误率较高，40%。为了得到更好的分类结果，通过交叉验证进行剪枝调整决策树复杂度。

3.2 剪枝优化模型

如果后续分析的目的是提高分类预测的准确性，则常使用分类错误率作为剪枝(pruning)的选择标准。

# 3.2.1 cross-validation 优化模型
set.seed(12345)
cv.tre = tree::cv.tree(tre,
                 FUN = prune.misclass, # prune.tree，prune.misclass可选。
                 K=10 # K folds,可根据样本数目调整，50能被10整除。
                 ) # K值设置不同，结果会有很大差异，可以多尝试几个K值。
names(cv.tre) # 输出结果
cv.tre$size # 每个树的终端节点数目
cv.tre$dev # cross-validation error rate
cv.tre$k # cost-complexity 参数值
​
## 绘图选择最佳终端节点数
par(mfrow =c(1,2))
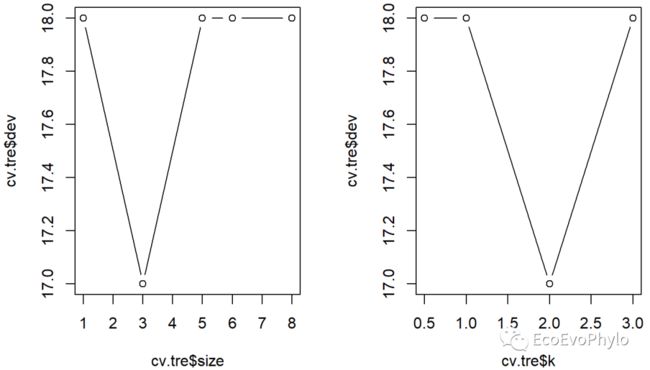
plot(cv.tre$size,cv.tre$dev,type="b")
plot(cv.tre$k,cv.tre$dev,type = "b") # 检测具有最低交叉错误率的终端节点的数量。
​

图14|交叉验证结果，reg.cv。size：每个树的终端节点数目；dev：cross-validation error rate；k：cost-complexity 参数值。

图15|交叉验证结果绘图。结果显示在终端节点数为3的时候误差率最低。当最低错误率，具有几个不同的终端节点数时，可以秉承简单模型的原则，选择最小的终端节点。也可以根据绘图结果，选择合适自己数据的终端节点数。当终端节点为1才有最低误差时，就选次一级的终端节点数。

# 3.2.2 使用prune.misclass()修剪决策树，设置终端节点为4
##通过递归地“剪裁”最不重要的拆分来确定所提供树的子树
##"剪枝"结果必须是决策树的子树，所以有时输出的子树终端节点并不一定等于设置的best值。
prune.tre = prune.tree(tre,
                       best = 3,
                       method = "misclass") # deviance和misclass可选。
summary(prune.tre)
plot(prune.tre)
text(prune.tre,pretty = 0)
​
# 3.2.3 修剪树预测测试数据集--提高分类结果准确率(所有分类正确的样本/样本总数)
## 增加终端节点的数量，反而会降低分类准确率
library(caret)
tre.pred = predict(prune.tre,test.spe[-c(1,2)],type = "class")  
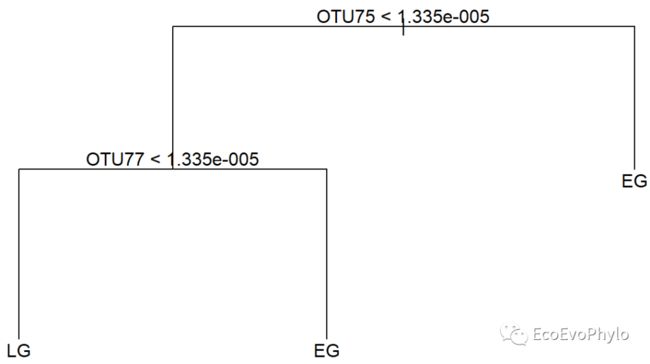
caret::confusionMatrix(tre.pred,test.spe[,2]) # 分类准确率为36%,剪枝后准确率反而降低了。

图16|剪枝后分类决策树，prune.tre。树生长总是从左侧开始。经过剪枝的分类树并不总是会提高分类正确率，有时还会降低分类正确率。比如此数据就是如此。分类争取率也比较低，说明数据不适合决策树模型。

微信公众号后台回复“决策树-tree”或QQ群文件获取数据及代码。

机器学习-多元分类/回归决策树模型(tree包)

参考资料：

James, Gareth, Daniela Witten, Trevor Hastie和Robert Tibshirani. An Introduction to Statistical Learning. 卷 103. Springer Texts in Statistics. New York, NY: Springer New York, 2013. https://doi.org/10.1007/978-1-4614-7138-7.

《精通机器学习：基于R》第二版

统计学：从数据到结论 第4版，吴喜之编著，2013，中国统计出版社。

---

推荐阅读

R绘图-物种、环境因子相关性网络图(简单图、提取子图、修改图布局参数、物种-环境因子分别成环径向网络图)

R统计绘图-分子生态相关性网络分析(拓扑属性计算，ggraph绘图)

R中进行单因素方差分析并绘图

R统计绘图-多变量单因素非参数差异检验及添加显著性标记图

R统计绘图-单因素Kruskal-Wallis检验

R统计绘图-单、双、三因素重复测量方差分析[Translation]

R统计-多变量单因素参数、非参数检验及多重比较

R统计-多变量双因素参数、非参数检验及多重比较

R绘图-KEGG功能注释组间差异分面条形图

R绘图-相关性分析及绘图

R绘图-相关性系数图

R统计绘图-环境因子相关性热图

R绘图-RDA排序分析

R统计-VPA分析(RDA/CCA)

R统计绘图-RDA分析、Mantel检验及绘图

R统计-PCA/PCoA/db-RDA/NMDS/CA/CCA/DCA等排序分析教程

R统计-正态性分布检验[Translation]

R统计-数据正态分布转换[Translation]

R统计-方差齐性检验[Translation]

R统计-Mauchly球形检验[Translation]

R统计绘图-混合方差分析[Translation]

R统计绘图-协方差分析[Translation]

R统计绘图-RDA分析、Mantel检验及绘图

R统计绘图-factoextra包绘制及美化PCA结果图

R统计绘图-环境因子相关性+mantel检验组合图(linkET包介绍1)

R统计绘图-随机森林分类分析及物种丰度差异检验组合图

机器学习-分类随机森林分析(randomForest模型构建、参数调优、特征变量筛选、模型评估和基础理论等)

---