GNN-CS224W: 3 Node Embeddings

graph representation learning

Automaticly learning efficient task-independent feature for machine learning with graphs，从而避免了特征工程

why embedding？

1. Similarity of embeddings between nodes indicates their similarity in the network.
2. Encode network information
3. Task independent, Potentially used for many downstream predictions

a simple pattern of Learning Node Embedding

1. Encoder: maps from nodes to embeddings

   $ENC(v)=z_v$, 输入为node，输出为node的embedding，

   例如一种简单的方式为给每个node定义一个向量，用node取embedding时直接执行embedding lookup操作

2. Define a node similarity function (i.e., a measure of similarity in the original network)

   $similarity(v,u)$

   一个计算node similarity的function，输入为没有转化为embedding的、original network的node，输出为2个node的相似度

3. Decoder: maps from embeddings to the similarity score

   计算两个node的embedding的similarity，

   例如可以用embedding向量的内积来表示相似度，即$z_v^T{z}_u$

4. 优化encoder的参数使得 (优化目标)：$similarity(v,u)=z_v^T{z}_u$

为什么向量内积可以表示相似度？

假设有N个向量，要找出和向量1最相似的向量。

依次计算向量2到N和向量1的内积。

内积=向量1的模 * 向量n在向量1上投影的长度

对所有向量计算的内积来说，向量1的模不变，那内积最大的就是在向量1上投影长度最大的向量

投影长度表示在向量1方向上的分量，可以认为是相似度。

How to define Node similarity

Random Walk

Notation:
$z_u$: The embedding of node u
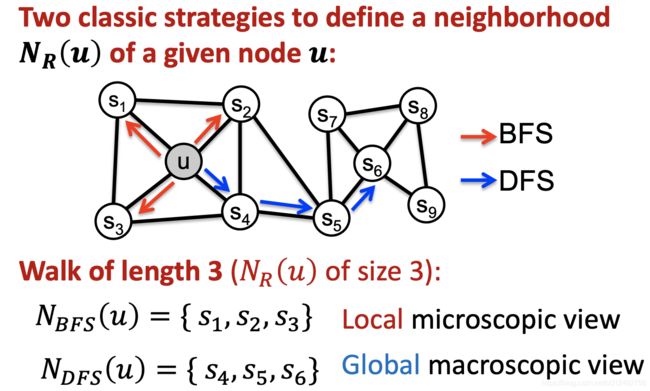
$P(v|z_u)$: The (predicted) probability of visiting node v on random walks starting from node u
$N_R(u)$: neighborhood of u obtained by some random walk strategy R

What is random walk

Intuition: if random walk starting from node u visits v with high probability, u and v are similar (high-order multi-hop information)，所以用这种方法得到 node similarity function

如果边没有权重，访问u的neighbor完全随机，则$p(v|u)$大表示v和u距离近；如果边有权重，且将权重大的选择的可能性大，则$p(v|u)$大表示v离u近或者v到u的路径权重较大，或者又近权重又大。总之$p(v|u)$大则u和v的联系越紧密。

优点：

1. incorporates both local and higher-order neighborhood information
2. Efficiency: Do not need to consider all node pairs when training; only need to consider pairs that co-occur on random walks

How to learn Random Walk Embeddings

given $G=(V,E)$, goal is to learn $f(u)=z_u$

步骤

1. Run short fixed-length random walks starting from each node u in the graph using some random walk strategy R

2. For each node u collect $N_R(u)$, the multiset of nodes visited on random walks starting from u

   multiset的意思是一个node可以出现多次。
   ( 应该意思是把所有random walk path中出现过的节点都放到一个集合里，同一个元素可以出现多次，$P_R(v|u)=\frac{v出现的总次数}{所有节点出现的总次数}$。 括号内的部分不适用于这里，但是是一个有用的思想)

   到目前为止做到了Estimate probability of visiting node v on a random walk starting from node u using some random walk strategy R, 即 $P_R(v|u)$ (概率没有用到)

3. Optimize embeddings according to: Given node u, predict its neighbors $N_R(u)$

   Maximize log-likelihood objective: $$\underset{f}{\max }\sum _{u\in V}\log P(N_R(u)|z_u)$$

   其中$P(N_R(u)|z_u)=\prod _{v\in N_R(u)}P(v|z_u)$，$N_R(u)$表示从u出发的random walk path中出现过的点，$P(v|z_u)$表示从节点u触发的random walk 到达节点v的概率，也就是u和v的相关度。

   $$P(v|z_u)=\frac{\exp z_u^T{z}_v}{\sum _{n\in V}\exp z_u^T{z}_n}$$

   要注意的是$v\in N_R(u)$并不是图里所有的节点，而概率$P(v|z_u)$计算的范围是全部节点，即$\sum _{v\in V}P(v|z_u)=1$。 这里以最大化$v\in N_R(u)$的概率为目标就是要让和u相关的节点的概率变大，从而encode图的信息。

   再将最大化改为负的最小化，则优化目标可以等价于最小化下式：

   $$L=\sum _{u\in V}\sum _{v\in N_R(u)}-\log \frac{\exp z_u^T{z}_v}{\sum _{n\in V}\exp z_u^T{z}_n}$$

计算优化 Negative Sampling

上面的objective复杂度过高了，是$O(|V{|}^2)$
（第一个|V|表示式子的第一层循环，第二个|V|表示概率的分母的循环，实际的图中，embedding dim和$N_R(u)$相比节点数量非常小，所以忽略不计了）

计算概率时的底数$\sum _{n\in V}\exp z_u^T{z}_n$占了很大的计算量

使用negative sampling来近似概率：用列举的K个negative sample来近似的计算概率，而不用计算全部节点。

$P(v|z_u)=\frac{\exp z_u^T{z}_v}{\sum _{n\in V}\exp z_u^T{z}_n}\approx \log (\sigma (z_u^T{z}_v))-\sum _{k=1}^K\log (\sigma (z_u^T{z}_k))$

How to choose negative sample?

节点选取概率 proportional to its degree (和degree成正比)，即degree越大，被选择的概率越大

How to choose K?

Higher K gives more robust estimates
Higher K corresponds to higher bias on negative events
In practice K =5-20

问题：

1. 为什么要选择degree大的node？
2. Higher K corresponds to higher bias on negative events？

How to random walk

DeepWalk

Simplest idea: Just run fixed-length, unbiased random walks starting from each node

But such notion of similarity is too constrained

Node2vec

Idea: use flexible, biased random walks that can trade off between local and global views of the network

实现方法

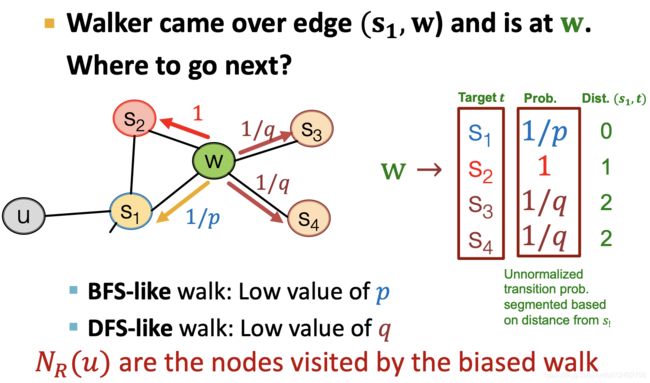
方法名：Biased 2nd-order random walks（因为它会记住是从哪个节点过来的）

用两个参数来调节random walk 运行的倾向:

Return parameter $p$: Return back to the previous node.用来调节返回到上一个节点的倾向大小

In-out parameter $q$: Moving outwards (DFS) vs. inwards (BFS). 用来调节向远处和近处的倾向，Intuitively, $q$ is the “ratio” of BFS vs. DFS.

实际步骤：

为什么是线性时间复杂度？

1. 步骤1的复杂度是O(1)，因为只需要指定参数$p$和$q$
2. 步骤2中，一个图中节点的数量通常非常大，而每个节点的path数量$r$、$l$和节点数量相比非常小，所以可以时间复杂度为O(number of nodes)
3. 步骤3中，优化时涉及的embedding dim、$N_R(u)$的数量和节点数量相比都要少很多，所以也可以认为时间复杂度是O(number of nodes)

other random walk ideas

Different kinds of biased random walks:

1. Based on node attributes (Dong et al., 2017).
2. Based on learned weights (Abu-El-Haija et al., 2017)

Alternative optimization schemes:

1. Directly optimize based on 1-hop and 2-hop random walk probabilities (as in LINE from Tang et al. 2015).

Network preprocessing techniques:

1. Run random walks on modified versions of the original network

Matrix factorization

(connection between matrix factorization and node embedding)

这一小节的内容讲的是求node embedding的过程可以被当做求matrix factorization

在上面的a simple pattern of Learning Node Embedding中，

1. 定义encode 的方法为给每个node初始化一个向量，则可以得到一个矩阵$Z$，size为(embed_dim, node_num)
2. 定义node similarity的计算方式为如果两个node之间有边则相似度为1，如果没有则相似度为0，则adjacency matrix $A$可以代表node之间的similarity，$A_{u,v}=1$则表示节点$u$和$v$相似，$A_{u,v}=0$则表示节点$u$和$v$不相似。
3. 定义decoder，两个node embedding相似度定义为 $z_v^T{z}_u$，则所有节点之间相似度可以表示为$Z^{T}Z$，size=(node_num, node_num)
4. 则优化目标为使得$Z^{T}Z=A$

$A=Z^{T}Z$可以被当做一个matrix $A$的factorization

但是精确的分解$A=Z^{T}Z$是不可能的(视频里是这么讲的，不知道为什么)

所以通过用梯度下降求$\underset{Z}{\min }||A-Z^{T}Z|{|}_2$来近似的求解

DeepWalk and node2vec虽然比上面的方法复杂，但是也可以被当做matrix factorization

详细描述见Network Embedding as Matrix Factorization: Unifying DeepWalk, LINE, PTE, and node2vec

有需要再回来看

问题：知道node embedding等价于matrix factorization的意义是什么？

Embedding Entire Graph

Entire Graph(subgraph) Embedding的用途举例：Classifying toxic vs non-toxic molecules; Identifying anomalous graphs

以下为获取Entire Graph(subgraph) Embedding 的方法：

sum (or average) the node embeddings in the (sub)graph

virtual node

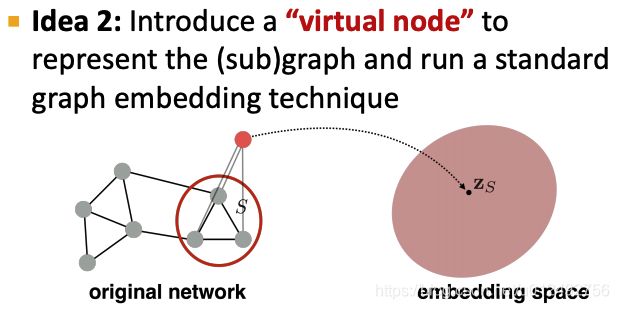
使用virtual node的embedding当做(sub)graph 的embedding

virtual node应该和哪些node连接？

应该和要获取的subgraph或者graph的所有节点连接

Anonymous Walking Embedding

这个方法无法理解
用各类Anonymous Walk的概率分布向量表示graph是可以理解的，但是用随机取的多个Anonymous Walk序列的顺序来获得embedding无法理解，序列之间的顺序应该没有关系

What is Anonymous Walking

如上图所示，所进行的random walk得到的path是不知道node的identity的，所以是Anonymous
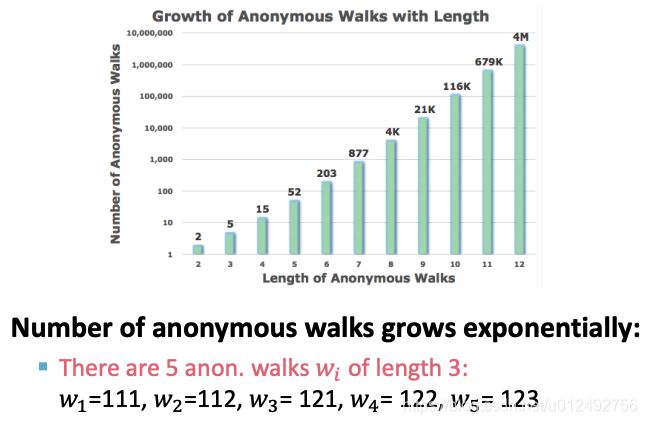这里长度为3的anonymous walk 的意思是一共走3步，111的意思是3步都经过同一个节点，112的意思是前2步经过同一个节点，第3步经过了另一个节点，123的意思是3步分别经过不同的节点。

从不同节点出发的长度为3的anonymous walk都有可能包括这5种情况。

How to use Anonymous Walking

1. Simulate all anonymous walks of $l$ steps and record their counts，generate independently a set of $m$ random walks

   How many random walks do we need?（$m$ 的大小应该是多少？）

   We want the distribution to have error of more than $\epsilon$ with prob. less than $\delta$:

   $m=[\frac{2}{{\epsilon }^2}(\log (2^{\eta }-2)-\log \delta )]$

   使用上面的公式来计算m，公式包括2个参数$\epsilon$和 $\delta$；
   $\eta$为长度为$l$的anonymous walk一共有多少种，一旦$l$确定，$\eta$是一个确定的值

   例如$l=7$时$\eta =877$，我们设$\epsilon =0.1$，$\delta =0.01$，则带入公式得$m=122500$

   问题：为什么要这么设置m？$\epsilon$和 $\delta$代表了什么？

2. Represent the graph as a probability distribution over these walks

   假设step数量$l$是确定的，则anonymous walk数量$\eta$也是确定的，从1中可以得到每一种anonymous walk的数量。

   将anonymous walk的种类当做一个变量，每一种为变量的一个值，则变量一共有$\eta$个可能的取值。我们知道每一种anonymous walk出现的次数以及总的次数，就可以得到该变量每一个取值的概率。将这个变量的概率分布作为Graph的表示。

   变量的概率分布可以表示为一个向量，向量每一位表示一种可能的anonymous walk，每一位上的值表示这种anonymous walk的概率。

   例如假设$l=3$，Then we can represent the graph as a 5-dim vector, Since there are 5 anonymous walks $w_i$ of length 3: 111, 112, 121, 122, 123。向量第0维表示111出现的概率，第1维表示112出现的概率…

Learn walk embeddings

利用anonymous walk学习整个graph的embedding $z_G$和每个anonymous walk sample的embedding $Z=\{z_i:i=1,\cdots ,m\}$，$m$为所有模拟得到的 anonymous walk 数量，不是固定长度的anonymous walk种类。

方法

将从节点$u$出发的所有anonymous walk当做一个序列$w_0,w_1,\cdots$。

指定序列的上下文窗口大小$\Delta$，用一个元素的上下文窗口内的其他元素预测它自己。例如$\Delta =1$，用$w_0,w_2$来预测$w_1$

调整$z_G$和$Z$使得在给定上下文的情况下实际发生的anonymous walk $w_i$的概率最大化。

以下为objective function：

$$\underset{Z,d}{\max }\sum _{u\in V}\frac{1}{T_u}\sum _{t=\Delta }^{T_u-\Delta }\log P(w_t|\{w_{t-\Delta },\cdots ,w_{t+\Delta },z_G\})$$

其中$T_u$表示从节点$u$出发的anonymous walk的数量

$$P(w_t|\{w_{t-\Delta },\cdots ,w_{t+\Delta },z_G\})=\frac{\exp (y(w_t))}{{\sum }_{i=1}^{\eta }\exp (y(w_i))}$$

$\eta$为所有可能的anonymous walk的种类，式子表示在所有可能的anonymous walk的种类中，这一个的概率。这里需要用到negative sampling来近似的计算

$$y(w_t)=b+U\cdot (cat(\frac{1}{2\Delta }\sum _{i=-\Delta }^{\Delta }{z}_i,z_G))$$

其中$b$、$U$为可学习的参数，cat表示向量拼接，$\frac{1}{2\Delta }\sum _{i=-\Delta }^{\Delta }{z}_i$表示上下文向量求平均

问题：

1. 每次sample的anonymous walk有关系吗？不是独立的吗？怎么可以用这个来预测？
2. 如果$eta$表示可能的anonymous walk种类，那么分母中的$y(w_t)$相加的上下文是什么？

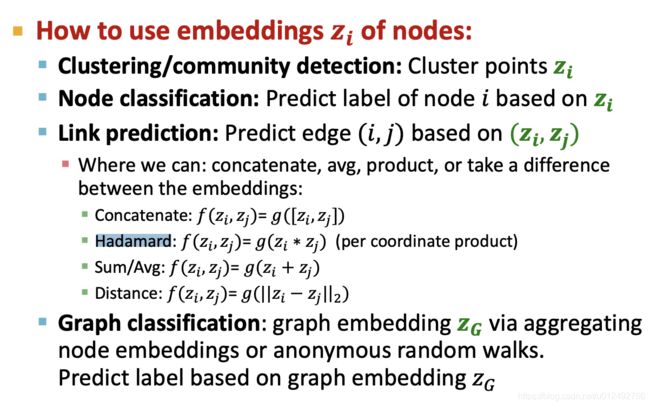
How to use embeddings

limitations

1. Cannot obtain embeddings for nodes not in the training set

2. Cannot capture structural similarity
   
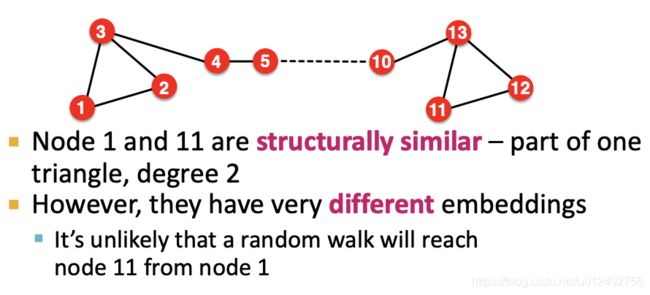
   DeepWalk 和Node2vec只考虑了节点是否临近，graph的结构完全没有考虑

3. Cannot utilize node, edge and graph features
   这里的node embedding 方法只考虑了从数据中抽象出来的graph信息，只利用了graph里node的邻接关系，而没有用到graph里的node、edge、 graph本身所有具有的信息，例如protein properties in a protein-protein interaction graph

Solution to these limitations: Deep Representation Learning and Graph Neural Networks

问题

1. 优化目标是一个回归吗（embedding相似度要映射到定义的相似度）？还是相似就越大越好，不相似就越小越好？
   答案是后者
2. anonymous walk $w_i$表示的是第i种 anonymous walk吗？
   $w_i$指的是实际sample出来的anonymous walk，i不对应种类，而是第i次sample的anonymous walk