GNN-CS224W: 17 Scaling Up GNNs

Graphs in model application

applications

• Recommender systems:
  Amazon, YouTube 等
  要预测用户对item(商品、视频)是否感兴趣 (link prediction)
  还要预测用户、item的类型(node classification)
  数据量级很大
• Social networks
  Facebook, Twitter, Instagram等
  要做 Friend recommendation (link level task)
  User property prediction, 广告等 (node level task)
  数据量级很大
• Academic graph
  Microsoft Academic Graph，一个学术论文的graph，可以做的任务如下(远不只下面3个)
  Paper categorization (node classification)
  Author collaboration recommendation (link prediction)
  Paper citation recommendation (link prediction)
• Knowledge Graphs (KGs)
  Wikidata，Freebase等
  任务有 KG completion， Reasoning等

things in common

Large-scale:

• nodes ranges from 10M to 10B.
• edges ranges from 100M to 100B

难点 in Large-scale graph

Naïve full-batch

GPU内存不够，CPU计算太慢

传统 mini-batch 中每个batch会缺失大量边

海量的数据导致不可能一次性把所有节点都输入模型进行训练，所以必须拆分成mini-batch

每个batch 是 randomly sample 得到的，这会导致每个sample得到的node几乎都 isolated from each other

而GNN需要 aggregate neighboring node features.

解决办法

Small subgraphs in each mini-batch

Neighbor Sampling [Hamilton et al. NeurIPS 2017]

GraphSage提出来的方法

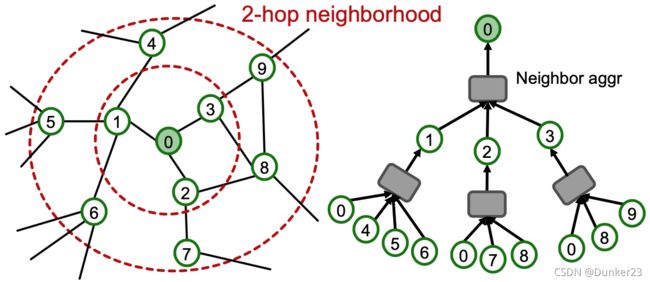
Key insight: the -hop neighborhood

To compute embedding of a single node, all we need is the -hop neighborhood
(which defines the computation graph)

如下图所示，要得到node 0的embedding，只需要红色虚线圈内的节点即可，无论整个图有多大，其他的节点都不需要

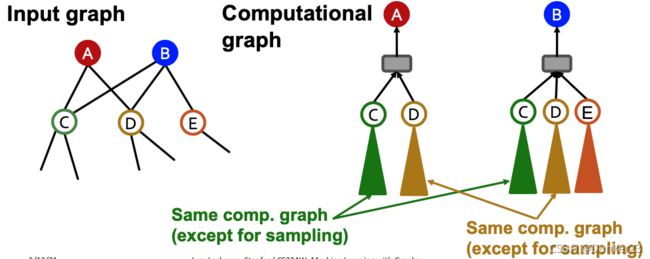
Given a set of different nodes in a mini-batch,we can generate their embeddings using computational graphs. Can be computed on GPU!

问题：怎么实现？给每个node一个单独的computational graph吗？这样能并行吗？

问题：每个节点都要一起训练embedding，每条边都是依赖节点存在的，那每个节点的K hop一定包含了每条边，这样就什么也省不了？

still computational expensive

• Computation graph becomes exponentially large with respect to the layer size .
• Computation graph explodes when it hits a hub node (high-degree node).

At most neighbors at each hop

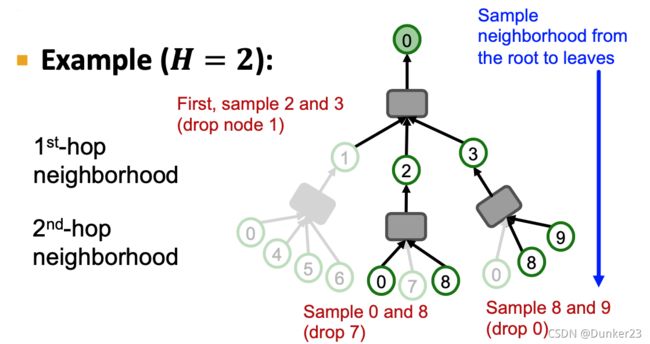
Key idea: Construct the computational graph by (randomly) sampling at most neighbors at each hop.

因为限制在了H，所以computational graph每一层都不会太大，所以网络可以达到比较深。

-layer GNN will at most involve ${\prod }_{k=1}^K{H}_k$ leaf nodes in computational graph

Remarks

Trade-off in sampling number

Smaller leads to more efficient neighbor aggregation, but results in more unstable training due to the larger variance in neighbor aggregation.

Computational time

Even with neighbor sampling, the size of the computational graph is still exponential with respect to number of GNN layers .

Increasing one GNN layer would make computation times more expensive.

How to sample the nodes

Random sampling: fast but many times not optimal (may sample many “unimportant” nodes)

Natural graphs are “scale free”, sampling random neighbors, samples many low degree “leaf” nodes.

Random Walk with Restarts:
Compute Random Walk with Restarts score $R_i$ starting at the interest node
At each level sample neighbors with the highest $R_i$

This strategy works much better in practice.

Issues

• The size of computational graph becomes exponentially large w.r.t. the number of GNN layers.

• Computation is redundant, especially when nodes in a mini-batch share many neighbors.
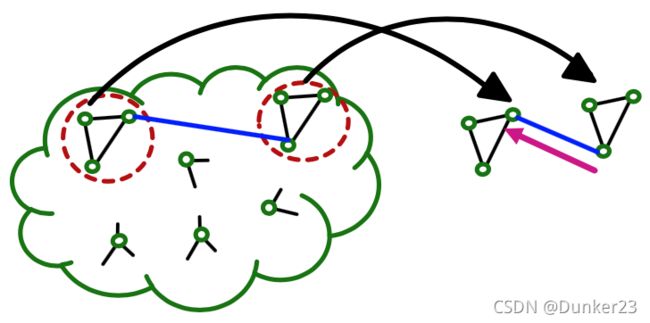
  如下图，计算A和B时，对C、D的同样的message passing操作要计算2次
  

  一个解决办法：HAG(hierarchical aggregation graphs)，找到重复计算的内容，然后只计算一次。细节课程里没涉及
  另一个解决办法是 Cluster GCN，问题：看起来Cluster GCN并没有解决这个问题

Cluster-GCN [Chiang et al. KDD 2019]

Key Idea

Full batch GNN

all the node embeddings are updated together using embeddings of the previous layer.

In each layer, only $2\times (edge\_num)$ messages need to be computed. 因为每条edge要分别向两个节点计算message

For -layer GNN, only $K\times 2\times (edge\_num)$ messages need to be computed.

GNN’s entire computation is only linear in #(edges) and #(GNN layers). Fast !

The layer-wise node embedding update allows the re-use of embeddings from the previous layer.
This significantly reduces the computational redundancy of neighbor sampling.
Of course, the layer-wise update is not feasible for a large graph due to limited GPU memory.

意思理解：好像neighbor sampling里每个node的computational graph是分别计算的，假设一个node有两个neighbor，这两个neighbor的computational graph里因为是每层随机取H个，这一个node不一定在neighbor的计算图里。而且好像每个computational graph都是随机每层取H个，所以同样一个node，在同一层，在不同的computational graph里的embedding可能不一样，所以不能重用。需要具体去看怎么实现的，会帮助理解。

问题: 没看懂，不是都可以re-use of embeddings from the previous layer吗？有我没有理解的内容？如果Neighbor sampling时存在重复计算，那这里也存在，甚至更多

问题：这里的意思是先算每个node的message，再按computational graph做aggregate吗？这样算的话确实去掉了重复计算

问题：这是因为GCN可以写成矩阵的形式所带来的计算优势吗？其他的GNN可以这样吗？需要从其他GNN的实现方式来看

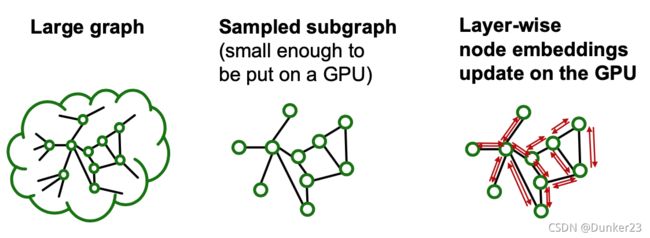
sample a small subgraph of the large graph

Key idea: We can sample a small subgraph of the large graph and then perform the efficient layer-wise node embeddings update over the subgraph.

What subgraphs are good for training GNNs?

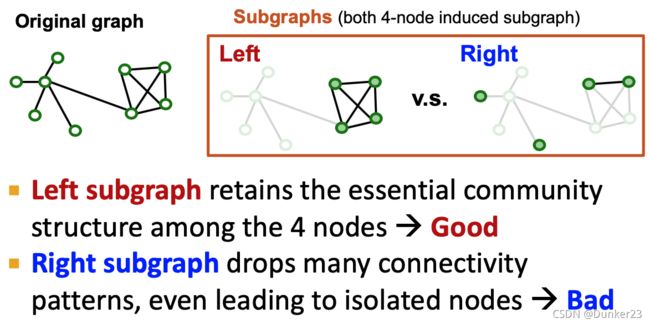
Subgraphs should retain edge connectivity structure of the original graph as much as possible.
This way, the GNN over the subgraph generates embeddings closer to the GNN over the original graph.

decomposed into small communities.

Real-world graph exhibits community structure
A large graph can be decomposed into many small communities.

Key insight [Chiang et al. KDD 2019]: Sample a community as a subgraph. Each subgraph retains essential local connectivity pattern of the original graph.

vanilla Cluster-GCN

two steps: Pre-processing and Mini-batch training

Pre-processing

Given a large graph, partition it into groups of nodes (i.e., subgraphs).

We can use any scalable community detection methods, e.g., Louvain, METIS

Notice: Between-group edges are dropped; group之间没有重合的 node; 所有node都在某一个group里

Mini-batch training

Sample one node group at a time. Apply GNN’s message passing over the induced subgraph. 一次只计算一个group of nodes

Issues

• The induced subgraph removes between- group links.
  As a result, messages from other groups will be lost during message passing, which could hurt the GNN’s performance.
• Graph community detection algorithm puts similar nodes together in the same group.
  Sampled node group tends to only cover the small-concentrated portion of the entire data.
• Sampled nodes are not diverse enough to be represent the entire graph structure
  • As a result, the gradient averaged over the sampled nodes becomes unreliable
  • Fluctuates a lot from a node group to another. In other words, the gradient has high variance.
  • Leads to slow convergence of SGD

Advanced Cluster-GCN

Solution: Aggregate multiple node groups per mini-batch.

2steps：

1. Partition the graph into relatively-small groups of nodes. 比以前的更小的subgraph

2. For each mini-batch:

   • 随机取一定数量的groups，并把它们合成一个大的group
   • 保留between-group edges

   问题：这里小group之间的edge是本来就存在的还是后来加的？看起来是保留的原有的edge，额外增加link，相当于改变了graph，应该不能这样做。

The rest is the same as vanilla Cluster-GCN

Why does the solution work?

more representative of the entire nodes. Leads to less variance in gradient estimation.

Includes between-group edges, so Message can flow across groups.

Comparison of Time Complexity

Neighbor Sampling

一共有 nodes，每层最多sample H个neighbor， 一共K 层 GNN，
则 the cost is $M\times H^K$

Cluster-GCN

一个subgraph共有 nodes，每个节点的平均degree为$D_{avg}$，-layer GNN，
则 the cost is $K\times M\times D_{avg}$

Comparison

Assume $H=\frac{D_{avg}}{2}$. In other words, 50% of neighbors are sampled.

Then, Cluster-GCN is much more efficient than neighbor sampling, K的线性复杂度比指数复杂度低很多

但是，通常在Neighor Sampling时会将H设置为 $D_{avg}$的2到3倍，因为K可以不用很大，复杂度也就不会太高，所以 Neighor Sampling 更常用。具体使用得看dataset的情况

simplifies a GNN into feature-preprocessing operation

(can be efficiently performed even on a CPU)

Simplified GCN [Wu et al. ICML 2019]

Wu et al. demonstrated that the performance on benchmark is not much lower by removing the non-linear activation from the GCN. 意思应该是去掉non-linear activation后效果不会降低太多， 论文里应该有细节。

Simplified GCN 因为更简单了，所以可以适用于数据量更大的情况

推导过程

则去掉ReLU可以得到
$$H^{(K)}={\tilde{A}}^{K}X{W}^T$$

${\tilde{A}}^K$相当于是从节点出发，K步能到达的节点的reachable matrix

${\tilde{A}}^K$也不包含任何参数，可以提前计算， Do $X\leftarrow \tilde{A}X$ for K times, 则
$$H^{(K)}=\tilde{X}{W}^T$$

任务现在转化为了a linear transformation of pre-computed matrix

Back to the node embedding form:
$$h_v^{(K)}=W{\tilde{X}}_v$$

由上式可得，Embedding of node $v$ only depends on its own (pre-processed) feature

summary

simplified GCN consists of two steps：

1. Pre-processing step
   Pre-compute $\tilde{X}={\tilde{A}}^{K}X$. Can be done on CPU.
2. Mini-batch training step
   • For each mini-batch, randomly sample nodes
   • Compute their embeddings by $h_{v_i}^{(K)}=W{\tilde{X}}_{v_i}$
   • Use the embeddings to make prediction and compute the loss averaged over the data points
   • Perform SGD parameter update

计算速度会非常快，参数也非常少

comparison with other method

• Compared to neighbor sampling
  • Simplified GCN generates node embeddings much more efficiently (no need to construct the giant computational graph for each node).
• Compared to Cluster-GCN
  • Mini-batch nodes of simplified GCN can be sampled completely randomly from the entire nodes (no need to sample from multiple groups as Cluster-GCN does)
  • Leads to lower SGD variance during training.
• But the model is much less expressive.
  • simplified GCN’s expressive power is limited due to the lack of non-linearity in generating node embeddings.

performance

Surprisingly, in semi-supervised node classification benchmark, simplified GCN works comparably to the original GNNs despite being less expressive

原因：Graph Homophily

Many node classification tasks exhibit homophily structure, 例如 nodes connected by edges tend to share the same target labels

例如 社交网络里交流频繁的node之间更可能共享某些label，Two papers tend to share the same category if one cites another，Two users tend to like the same movie if they are friends in a social network

问题：什么是Graph Homophily ？应该是cluster内部的node比较类似

when will it work ?

决定node的预测结果的是 节点自己的特征和adajcency matrix相乘的K次，也即和node自己有连接的node的特征的融合

所以当graph具有局部同质性的时候，simplified GCN可以表现的很好