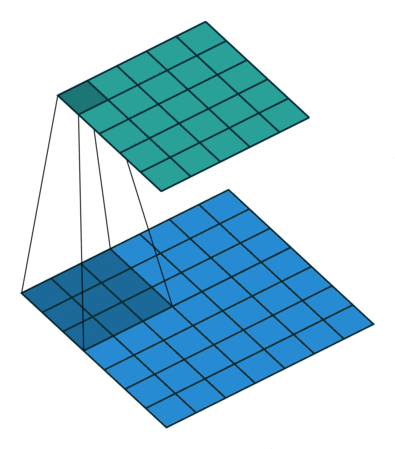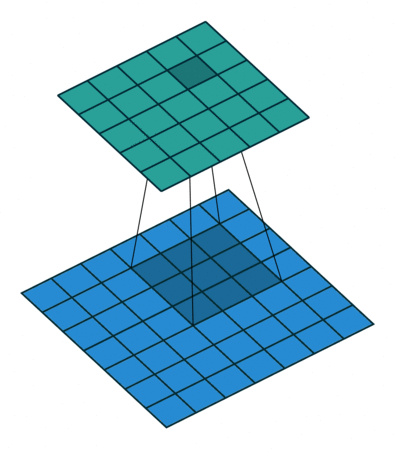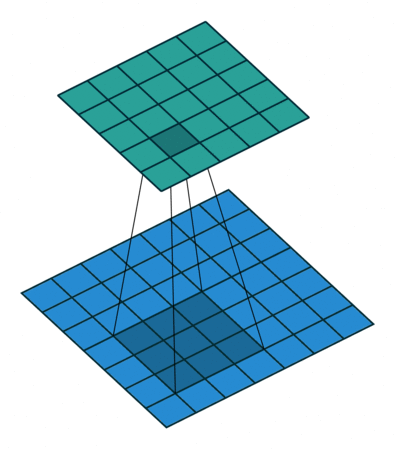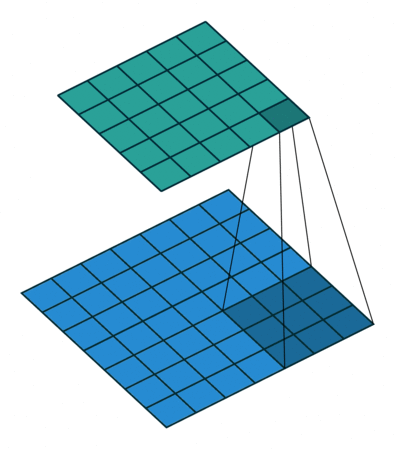
图像语义分割中的上采样(Upsampling)和下采样(subsampling)

最近在看到一篇论文中用到了transposed convolution，并出现了upsampling等概念，表示很迷。那么什么是upsampling ？

因此作出如下总结仅供自己学习理解。

---

1. 下采样（subsampled）

下采样：就是对卷积得到的 $FeatureMap$ 进行进一步压缩。通俗的所，实际上就是卷积层之间的池化操作。

作用： 通过最大池化或者平均池化从而减少了特征，减少了参数的数量，且降低了卷积网络计算的复杂度；实际上就是过滤作用小、信息冗余的特征，保留关键信息（而信息关键与否就体现在对应像素的value是否被激活的更大）。

下图左边是经过卷积得到的一个Feature Map，卷积后的每一个像素点我理解成：将原始图像中卷积核大小的所有像素点特征糅合到了一个像素点。

通过步长为 2 的最大池化，将被激活程度最大（value最大）的特征筛选出来，而其余相对较小的特征则被去掉，达到降低特征维度的作用。同时还增大了整个网络图所覆盖的感受野。

2. 上采样（upsampled）

就是将提取到的Feature Map进行放大， 从而以更高的分辨率进行显示图像。这里的方法图像放大，并不是简单地方法放大，也不是之前下采样的逆操作。
也就是说上采样放大后输出的图像和下采样之前的图像是不一样的。

常用的上采样方法有两种：

• 双线性插值
• 反卷积

首先看看什么是线性插值吧。

2.1 线性插值

其实线性插值¹是一种数学方法，有一阶、二阶、三阶，对应为单线性插值、双线性插值和三线性插值。三者不同之处在于：

• 单线性插值对应两点之间任意一点为插值；
• 双线性插值对应4点形成方形之间的任意一点作为插值；
• 三线性插值对应8点形成立方体内的任意一点作为插值。

2.2 单线性插值

已知中$P_1$点和$P_2$点，坐标分别为$(x_1,y_1)$、$(x_2,y_2)$，要计算$[x_1,x_2]$ 区间内某一位置 $x$ 在直线上的 $y$ 值.

该直线一定满足方程：

$$\frac{(y-y_1)}{(x-x_1)}=\frac{(y_2-y_1)}{(x_2-x_1)}$$

可以化简得到：
$$y=(\frac{x_2-x}{x_2-x_1})y_1+(\frac{x-x_1}{x_2-x_1})y_2$$

可以看到$y$的值与$y_1$和$y_2$的各自对应有关，并且对应系数$(\frac{x_2-x}{x_2-x_1})$和 $(\frac{x-x_1}{x_2-x_1})$决定了 $y_1$ 和 $y_2$ 分别对 $y$ 的贡献。

进一步细看，$x_1、x_2、y_1、y_2$均已知，则由 $x$ 值决定 $y$ 走向。

• 当 $x$ 越靠近 $x_1$,那么 $(\frac{x-x_1}{x_2-x_1})$的值就越小，则 $y_2$ 对 $y$ 的贡献越小，反而 $y_1$ 对 $y$ 的贡献越大，所以 $y$ 更加靠近 $y_1$ 的值。
• 当 $x$ 越靠近 $x_2$,那么 $(\frac{x_2-x}{x_2-x_1})$的值就越小，则 $y_1$ 对 $y$ 的贡献越小，反而 $y_2$ 对 $y$ 的贡献越大，所以 $y$ 更加靠近 $y_2$ 的值。

这是根据直线方程的定义求得的结论，但是我们现在在讨论插值。
即考虑如何在某一个坐标点上插入一个合理的像素值。

同样根据插入点与它周围像素点的距离远近，来分配不同权重，进行叠加。
将 $y_1$ 和 $y_2$ 换作对应点位置的像素值 即：$f(p_1)$ 和 $f(p_2)$ ，则公式可得：

$$f(p)=(\frac{x_2-x}{x_2-x_1})f(p_1)+(\frac{x-x_1}{x_2-x_1})f(p_2)$$

也就是说，插值点离哪一个像素点越近，就与那一个像素点更相关，则更近像素点的权重应当更大。

---

2.3 双线性插值

然后，根据单线性插值再来介绍下双线性插值方法²。

实际上就是先进行了 2 次横向的单线性插值，然后根据单线性插值的结果进行 1 次纵向的单线性插值。

首已知$Q_{11}(x_1,y_1)、Q_{12}(x_1,y_2)、Q_{21}(x_2,y_1)、Q_{22}(x_2,y_2)$ 四个点的坐标，设插值坐标点为$(x,y)$，像素为 $z$

现在固定 $x$ ,计算 $y$ 的位置。

• 首先根据$Q_{11}、Q_{21}$计算出$R_1(x,y_1)$的像素值;
• 再根据$Q_{12}、Q_{22}$计算出$R_2(x,y_2)$的像素值;
• 最后再依据$R_1$、$R_1$得到 $p$ 的像素插值$z$。

根据单线性插值的结论公式，可以直接得出结果1：
$$f(R_1)=(\frac{x_2-x}{x_2-x_1})f(Q_{11})+(\frac{x-x_1}{x_2-x_1})f(Q_{21})$$
$$f(R_2)=(\frac{x_2-x}{x_2-x_1})f(Q_{12})+(\frac{x-x_1}{x_2-x_1})f(Q_{22})$$

再根据$f(R_1)、f(R_2)$进行纵向单线性插值，可得结果2：
$$f(p)=(\frac{y_2-y}{y_2-y_1})f(R_1)+(\frac{y-y_1}{y_2-y_1})f(R_2)$$

将结果1代入结果2中，可得：

$$f(p)=(\frac{y_2-y}{y_2-y_1})(\frac{x_2-x}{x_2-x_1})f(Q_{11})+(\frac{y_2-y}{y_2-y_1})(\frac{x-x_1}{x_2-x_1})f(Q_{21})+(\frac{y-y_1}{y_2-y_1})(\frac{x_2-x}{x_2-x_1})f(Q_{12})+(\frac{y-y_1}{y_2-y_1})(\frac{x-x_1}{x_2-x_1})f(Q_{22})$$
可以简化得：
$$f(p)=w_{11}f(Q_{11})+w_{21}f(Q_{21})+w_{12}f(Q_{12})+w_{22}f(Q_{22})$$
其中$w_{11}、w_{21}、w_{12}、w_{22}$分别表示四个点对点$p$上像素的一个权重比，这是根据训练得出来的。

根据结果可得，双线性插值和前面提到的定义 （双线性插值对应4点形成方形之间的任意一点作为插值） 刚好对应。

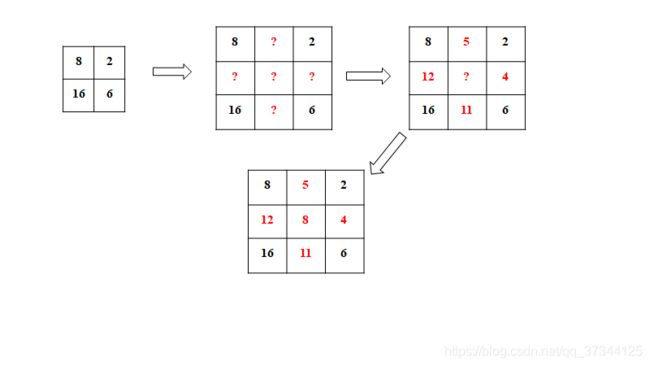
2.4 双线性插值举例

这里假设按照取平均的准则，进行插值计算，即$w_{11}、w_{21}、w_{12}、w_{22}$均为 $0.5$

2.5 插值法总结

在原有图像像素的基础上，在像素点之间采用合适的插值算法插入新的元素³。

插值就是在不生成像素的情况下增加图像像素大小的一种方法，在周围像素色彩的基础上用数学公式计算丢失像素的色彩（也有的有些相机使用插值，人为地增加图像的分辨率）。

所以在放大图像时，图像看上去会比较平滑、干净。但必须注意的是插值并不能增加图像信息。

---

2.6 转置卷积（Transposed Convolution）

其实转置卷积还有更通俗的说法，叫做反卷积(Deconvolution)。

转置卷积实际上是通过卷积运算实现分辨率还原。因为卷积操作中有权重参数，所以这是一种可以学习的方法，通过参数的学习实现输出图像尽可能与原图像相似。

和传统的卷积运算相比：

• 相同点：都是根据卷积核进行卷积运算；
• 不同点：普通卷积通过padding然后卷积是为了提取特征，使Feature Map变小，提取出更加复杂的特征；而在转置卷积中的stride存在不同，在输入图像的每两个像素之间增加大小为stirde的空像素，和空洞卷积的空洞操作是一样的。并且通过转置卷积，有使得Feature Map尺寸变大的效果。

即前者提取高级特征，后者放大高级特征。

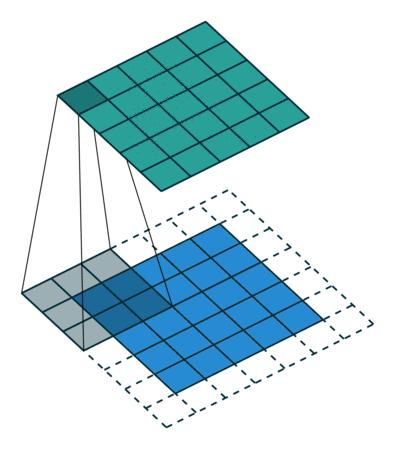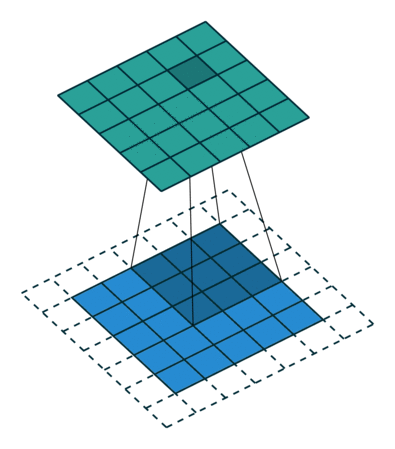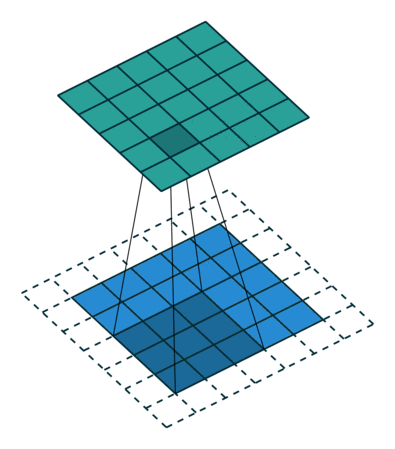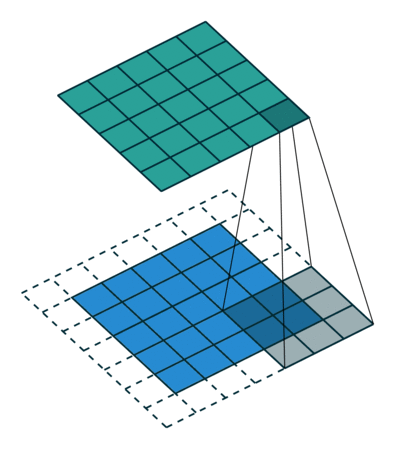
具体给一些常见的例子⁴：

No padding, no strides, transposed	Arbitrary padding, no strides, transposed	Half padding, no strides, transposed	Full padding, no strides, transposed
No padding, strides, transposed	Padding, strides, transposed	Padding, strides, transposed (odd)

可以注意到第一行的四张图都是no strides，所以和不同的卷积类似；

而第二行的strides设置为2，所以两两像素之间存在一个空像素，即 0 的个数为 $strides-1$。

这样对像素周围进行补0的方式就是最简单的反卷积。

另外也可以看看这一篇总结的反卷积，感觉写的不错，有对应的实际Demo。

但是这样的补0操作会使得像素边缘信息不断丢失。$FCN$ ⁵中通过相加的方式很好地解决了这类特征信息不足问题。

---

3. FCN (Fully Convolutional Networks)

全卷积神经网络(full Convolutional neural network, FCN)是一个普通的CNN，其中最后一个全连接层被另一个具有较大“感受野”的卷积层所取代。这样做是为了捕捉全局背景的整体信息(告诉我们图像中有什么，并且给出一些物体位置的粗略描述)。

如上图中，$image$ 为原始图像$（32\ast 32）$，有 $pool1、pool2、pool3、pool4、pool5$ 五次卷积得到的$FeatureMap$

首先看到 $pool5$,是通过原始图像经过了 5 次下采样操作，得到的$1\ast 1$的$FeatureMap$，包含了高纬度的特征信息。直接将该 $FeatureMap$ 通过上采样放大 32 倍，还原到原始图片大小，得到了$32x$ $upsampled$ $prediction$ 的结果，如下图红色箭头指向所示：

因为在 $FCN$ 中每下采样一次，图像的边缘信息在不断减少，而图像的更高维度特征则会被学习到，为了同时包含低纬度和高纬度特征图的的不同特点，因此提出了一个相加的操作。
也就是说不仅只考虑高纬度的$FeatureMap$ ，因此 $FCN$ 做出如下操作：

1. 将 $pool5$ 的特征进行两倍大小的上采样放大，即得到图中的$2x$ $upsampled$ $prediction$，此时的 $FeatureMap$ 大小和 $pool4$ 的大小一致；
2. 因为 $pool5$ 中保存了最高维度的特征信息，$pool4$ 中保存了次高维度的特征信息，然后将这两个$FeatureMap$ 进行相加；
3. 将相加的结果进行16倍的上采样放大，即得到图中的$16x$ $upsampled$ $prediction$，此时的 $FeatureMap$ 大小也和原始输入图像一致。

通过上面三个步骤得到的图像同时保存了 $pool4$ 和 $pool5$ 两个维度级别的特征。

依次类推，把 $pool3、pool4、pool5$ 的维度特征也进行叠加，然后对比各自不同叠加情况的预测效果，取最优情况，这就是 $FCN$ 最经典的一个原理流程。

最后其实我还是对转置卷积的运算有些不理解，如果有道友懂的可以一起聊聊，我也等后续理解了在进行补充吧！

---

1. 【数学】线性插值 ↩︎

2. 学无疑物-上采样之双线性插值法详解 ↩︎

3. 深度学习中的上采样 ↩︎

4. Convolution arithmetic ↩︎

5. Fully Convolutional Networks for Semantic Segmentation ↩︎