【动手学深度学习】李沐——多层感知机

多层感知机的从零开始实现

import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

# 初始化模型参数
num_inputs, num_outputs, num_hiddens = 784, 10, 256
W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2]


def relu(X):
    a = torch.zeros_like(X)
    return torch.max(X, a)


def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(X @ W1 + b1)  # @代表矩阵乘法的简写
    return H @ W2 + b2


loss = nn.CrossEntropyLoss(reduction='none')

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
plt.show()
d2l.predict_ch3(net,test_iter)
plt.show()

多层感知机的简洁实现

import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(), nn.Linear(256, 10))


def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)


net.apply(init_weights)


batch_size, lr, num_epochs = 256, 0.01, 10
loss = nn.CrossEntropyLoss(reduction='none')


train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

optimer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter,test_iter, loss, num_epochs, optimer)


plt.show()

权重衰减

简洁实现

net = nn.Sequential(nn.Linear(num_inputs, 1))
for param in net.parameters():
	param.data.normal_()
optimer = torch.optim.SGD([ {"params":net[0].weight,'weight_decay':wd},
{"params":net[0].bias}],lr=lr)

上面设置“weight_decay”为wd就是设置其使用权重衰减。

Dropout

一个好的模型需要对输入数据的扰动鲁棒，也就是不能够受噪声的影响。那么如果使用带有噪声的数据来学习的话，如果能够使得其不学习到噪声的那部分内容，那么也相当于是正则化。因此丢弃法(Dropout)就是在层之间加入噪音。

那么从定义方向出发，它就是无偏差的加入噪音，即对原本输入$xx$加入噪音得到${xx}^{\prime }$，希望其均值不变，即：
$$E[{xx}^{\prime }]=xx$$
那么丢弃法具体的做法是对每个元素执行如下扰动：
$$x_i^{\prime }=\{\begin{array}{l}0withprobablityp\\ \frac{x_i}{1-p}otherwise\end{array}$$
那么这样可以保证期望不变：
$$E[x_i^{\prime }]=p\times 0+(1-p)\times \frac{x_i}{1-p}=x_i$$
那么这个丢弃概率就是控制模型复杂度的超参数

具体是通常将丢弃法作用在多层感知机的隐藏层的输出上，即：

这是在训练过程中使用，它将会影响模型参数的更新，而在测试的时候并不会进行dorpout操作，这样能够保证确定性的输出。从实验上来说，它和正则化能够达到类似的效果。

那么Dropout放在隐藏层的输出，会将那些被置为0的神经元的权重在本次不进行更新，那么就可以认为是每一次Dropout都是从所有的隐藏层神经元中挑选出一部分来进行更新。

具体的实现直接调用nn.Dropout()层即可。

数值稳定性

在计算梯度时：

因为向量对向量的求导是矩阵，因此这么多次矩阵的运算可能会遇见梯度爆炸或者梯度消失的问题。

假设矩阵中的梯度大部分都是比1大一点的数，那么经过这么多次梯度计算就可能出现梯度过大而爆炸；那么梯度如果稍微小于1也就会经过这么多次迭代之后接近于0。

那么梯度爆炸就会带来如下的问题：

• 值超过了数值类型可以表示的范围
• 对学习率更加敏感
  • 当学习率比较大，乘上较大的梯度就更新程度比较大，难以稳定
  • 当学习率太小，那么可能导致在除开梯度爆炸的那些权重外的正常权重无法正常更新

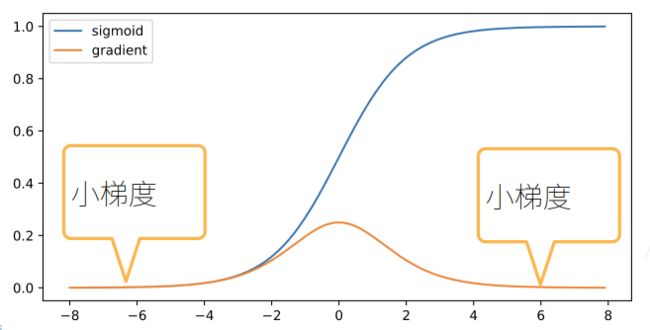
而对于梯度消失，例如采用sigmoid函数：

这么小的梯度在多个叠加之后就可能会出现梯度消失的问题。它的主要问题是：

• 也是超过表示范围，直接就使大部分梯度值为0，无法更新
• 训练因为梯度值为0，无法正常更新
• 对于底部层尤为严重，因为梯度是从输出层反向传播计算得到的，越到底部层，叠加的层数越多，梯度越可能消失，那就使得只有顶部层能够正常训练更新

那么如何使训练更加稳定的首要目标，就是让梯度值在合理的范围内，例如在某些算法中它们将梯度的乘法转换成加法，或者是对梯度进行归一化、裁剪等。但还有一种重要的方法就是合理的进行权重初始化，以及选择适合的激活函数。

具体来说，结论就是在对权重进行初始化的时候，让权重是从一个均值为0，方差为${\gamma }_t=\frac{2}{n_{t-1}+n_t}$中采样得到的。其中$n_{t-1}、n_t$代表该权重所连接的两个层的神经元的数目。因此需要根据层的形状来选择权重所服从分布的方差。

而激活函数经过推导，可以认为tanh(x)和ReLU(x)这两个激活函数能够具有较好的特性，而sigmoid(x)需要调整为$4\times sigmoid(x)-2$才能够达到与前两个相同的效果。

环境和分布偏移

1、分布偏移的类型

主要有以下几种偏移类型：

• 协变量偏移：指的是数据的分布$p(x)$发生了变化，例如在训练的时候用到的训练数据集分布$p_1(x)$和测试的时候用到的测试集分布$p_2(x)$不同，那么这就很难使得模型在测试数据集上表现好。不过这种变化还有一个架设计就是虽然输入的分布可能随时间发生变化，但是标签函数(即条件分布$P(y\mid x)$)不会改变。例如在训练的时候我们用真实的猫和狗来让机器学会分类，但是在测试的时候我们用的是卡通的猫和狗，这就是训练和测试两部分的数据集不相同，但是它们的标签函数是相同的，可以正确地对猫和狗进行标注。
• 标签偏移：指的是和协变量偏移相反的问题，因为这里假设标签边缘概率$P(y)$可以改变，但是类别条件分布$P(x\mid y)$在不同的领域之间保持不变。这里可以举一个例子就是预测患者的疾病，症状就是x，而所患的疾病就是标签y，那么疾病的相对流行率，或者说各种疾病之间的比例可能发生变化（即$P(y)$）可能发生变化，而对于某种特定疾病所对应的症状($P(x\mid y))$不会发生变化。
• 概念偏移：指的是标签的定义出现了变化。举个例子就是我们对于美貌的定义，可能会随着时间的变化而发生变化，那么这个“美貌”的标签的概念就发生了变化。

2、分布偏移纠正

首先需要了解什么是经验风险与实际风险：在训练时我们通常是最小化损失函数（不考虑正则化项），即：
$$\underset{f}{\min }\frac{1}{Num}\sum _{i=1}^{Num}loss(f(x_i),y_i)$$
这一项在训练数据集上的损失称为经验风险。那么经验风险就是为了来近似真实风险的，也就是数据的真实分布下的损失。然而在实际中我们无法获得真实数据的分布。因此一般认为最小化经验风险可以近似于最小化真实风险。

协变量偏移纠正

对于目前已有的数据集(x,y)，我们要评估$P(y\mid x)$，但是当前的数据$x_i$是来源于某些源分布$q(x)$(可以认为是训练数据集的分布)，而不是来源于目标分布$p(x)$(可以认为是真实数据的分布，或者认为是测试数据的分布)。但存在协变量偏移的假设即$p(y\mid x)=q(y\mid x)$。因此：
$$\iint loss(f(x),y)p(x)dxdy=\iint loss(f(x),y)q(y\mid x)q(x)\frac{p(x)}{q(x)}dxdy$$
因此当前我们需要计算数据来自于目标分布和来自于源分布之间的比例，来重新衡量每个样本的权重，即：
$${\beta }_i=\frac{p(x_i)}{q(x_i)}$$
那么将该权重代入到每个数据样本中，就可以使用加权经验风险最小化来训练模型：
$$\underset{f}{\min }\frac{1}{Num}\sum _{i=1}^{Num}{\beta }_{i}loss(f(x_i),y)$$
因此接下来的问题就是估计$\beta$。具体的方法为：从两个分布中抽取样本来进行分布估计。即对于目标分布$p(x)$我们就可以通过访问测试数据集来获取；而对于源分布$q(x)$则直接通过训练数据集获取。这里需要考虑到访问测试数据集是否会导致数据泄露的问题，其实是不会的，因为我们只访问了特征$x\sim p(x)$，并没有访问其标签y。在这种方法下，有一种非常有效的办法来计算$\beta$：对数几率回归。

我们假设从两个分布中抽取相同数据的样本，对于p抽取的样本数据标签为z=1，对于q抽取的样本数据标签为z=-1。因此该混合数据集的概率为：
$$\begin{gathered} P(z=1\mid x)=\frac{p(x)}{p(x)+q(x)} \\ \frac{P(z=1\mid x)}{P(z=-1\mid x)}=\frac{p(x)}{q(x)} \end{gathered}$$
因此如果我们使用对数几率回归的方法，即$P(z=1\mid x)=\frac{1}{1+exp(-h(x))}$（h是一个参数化函数，设定的），那么就有：
$${\beta }_i=\frac{P(z=1\mid x_i)}{P(z=-1\mid x_i)}=exp(h(x_i))$$
因此只要训练得到$h(x)$即可。

但上述算法依赖一个重要的假设：需要目标分布（测试集分布）中的每个数据样本在训练时出现的概率非零，否则将会出现$p(x_i)>0,q(x_i)=0$的情况。

标签偏移纠正

同样，这里假设标签的分布随时间变化$q(y)\ne p(y)$，但类别条件分布保持不变$q(x\mid y)=p(x\mid y)$。那么：
$$\iint loss(f(x),y)p(x\mid y)p(y)dxdy=\iint loss(f(x),y)q(x\mid y)q(y)\frac{p(y)}{q(y)}dxdy$$
因此重要性权重将对应于标签似然比率：
$${\beta }_i=\frac{p(y_i)}{q(y_i)}$$
因为，为了顾及目标标签的分布，我们首先采用性能相当好的现成的分类器（通常基于训练数据训练得到），并使用验证集计算混淆矩阵。那么混淆矩阵是一个$k\times k$的矩阵（k为分类类别数目）。每个单元格的值$c_{ij}$是验证集中真实标签为j，而模型预测为i的样本数量所占的比例。

但是现在我们无法计算目标数据上的混淆矩阵，因为我们不知道真实分布。那么我们所能做的就是**将现有的模型在测试时的预测取平均数，得到平均模型输出$\mu (\hat{y})\in R^k$，其中第i个元素为我们的模型预测测试集中第i个类别的总预测分数。

那么具体来说，如果我们的分类器一开始就相当准确，并且目标数据只包含我们以前见过的类别（训练集和测试集的拥有的类别是相同的），那么如果标签偏移假设成立，就可以通过一个简单的线性系统来估计测试集的标签分布：
$$Cp(y)=\mu (\hat{y})$$
因此若C可逆，则可得：
$$p(y)=C^{-1}\mu (\hat{y})$$

概念偏移纠正

这个很难用什么确切的方法来纠正。不过这种变化通常是很罕见的，或者是特别缓慢的。我们能够做的一般是训练时要适应网络的变化，使用新的数据来更新网络。

实战kaggle比赛：预测房价

import numpy as np
import pandas as pd
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
import hashlib
import os
import tarfile
import zipfile
import requests

DATA_HUB = dict()
DATA_URL = 'http://d2l-data.s3-accelerate.amazonaws.com/'


def download(name, cache_dir=os.path.join("dataset", "data_kaggle")):  # @save
    assert name in DATA_HUB, f"{name} 不存在于 {DATA_HUB}"
    url, shal_hash = DATA_HUB[name]
    os.makedirs(cache_dir, exist_ok=True)  # 按照第一个参数创建目录，第二参数代表如果目录已存在就不发出异常
    fname = os.path.join(cache_dir, url.split('/')[-1])
    if os.path.exists(fname):  # 如果已存在这个数据集
        shal = hashlib.sha1()
        with open(fname, 'rb') as f:
            while True:
                data = f.read(1048576)  # 这里进行数据集的读取，一次能够读取的最大行数为1048576
                if not data:  # 如果读取到某一次不成功
                    break
                shal.update(data)
        if shal.hexdigest() == shal_hash:
            return fname  # 命中缓存
    print(f'正在从{url}下载{fname}...')
    r = requests.get(url, stream=True, verify=True)
    # 向链接发送请求，第二个参数是不立即下载，当数据迭代器访问的时候再去下载那部分，不然全部载入会爆内存，第三个参数为不验证证书
    with open(fname, 'wb') as f:
        f.write(r.content)
    return fname


# 下载并解压一个zip或tar文件
def download_extract(name, folder=None):  # @save
    fname = download(name)
    base_dir = os.path.dirname(fname)  # 获取文件的路径，fname是一个相对路径，那么就返回从当前文件到目标文件的路径
    data_dir, ext = os.path.splitext(fname)  # 将这个路径最后的文件名分割，返回路径+文件名，和一个文件的扩展名
    if ext == '.zip':  # 如果为zip文件
        fp = zipfile.ZipFile(fname, 'r')
    elif ext in ('.tar', '.gz'):
        fp = tarfile.open(fname, 'r')
    else:
        assert False, "只有zip/tar文件才可以被解压缩"
    fp.extractall(base_dir)  # 解压压缩包内的所有文件到base_dir
    return os.path.join(base_dir, folder) if folder else data_dir


def download_all():  # @save
    for name in DATA_HUB:
        download(name)


# 下载并缓存房屋数据集
DATA_HUB['kaggle_house_train'] = (  # @save
    DATA_URL + 'kaggle_house_pred_train.csv',
    '585e9cc93e70b39160e7921475f9bcd7d31219ce'
)

DATA_HUB['kaggle_house_test'] = (  # @save
    DATA_URL + 'kaggle_house_pred_test.csv',
    'fa19780a7b011d9b009e8bff8e99922a8ee2eb90'
)

train_data = pd.read_csv(download('kaggle_house_train'))
test_data = pd.read_csv(download('kaggle_house_test'))

# print(train_data.shape)
# print(test_data.shape)
# print(train_data.iloc[0:4,[0,1,2,3,-3,-2,-1]])

# 将序号列去掉,训练数据也不包含最后一列的价格列，然后将训练数据集和测试数据集纵向连接在一起
all_features = pd.concat((train_data.iloc[:, 1:-1], test_data.iloc[:, 1:]))

# 将数值型的数据统一减去均值和方差
numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index  # 在panda中object类型代表字符串
all_features[numeric_features] = all_features[numeric_features].apply(
    lambda x: (x - x.mean()) / (x.std())  # 应用匿名函数
)
# 在标准化数据后，所有均值消失，因此我们可以设置缺失值为0
all_features[numeric_features] = all_features[numeric_features].fillna(0)

# 对离散值进行处理
all_features = pd.get_dummies(all_features, dummy_na=True)  # 第二个参数代表是否对nan类型进行编码

# print(all_features.shape)

n_train = train_data.shape[0]  # 训练数据集的个数
train_features = torch.tensor(all_features[:n_train].values, dtype=torch.float32)  # 取出训练数据
test_features = torch.tensor(all_features[n_train:].values, dtype=torch.float32)  # 取出测试数据
train_labels = torch.tensor(train_data.SalePrice.values.reshape(-1, 1), dtype=torch.float32)  # 取出训练数据的价格列

loss = nn.MSELoss()
in_features = train_features.shape[1]  # 特征的个数


# 网络架构
def get_net():
    net = nn.Sequential(nn.Linear(in_features, 1))
    return net


# 取对数约束输出的数量级
def log_rmes(net, features, labels):
    clipped_preds = torch.clamp(net(features), 1, float('inf'))
    # 第一个为要约束的参数，第二个为最小值，第三个为最大值，小于最小值就为1
    rmse = torch.sqrt(loss(torch.log(clipped_preds), torch.log(labels)))
    return rmse.item()


# 训练的函数
def train(net, train_features, train_labels, test_features, test_labels, num_epochs, learning_rate,
          weight_decay, batch_size):
    train_ls, test_ls = [], []
    train_iter = d2l.load_array((train_features, train_labels), batch_size)  # 获取数据迭代器
    optimizer = torch.optim.Adam(net.parameters(), lr=learning_rate, weight_decay=weight_decay)
    # 这是另外一个优化器，它对lr的数值不太敏感，第三个参数代表是否使用正则化
    for epoch in range(num_epochs):
        for X, y in train_iter:
            optimizer.zero_grad()  # 梯度先清零
            l = loss(net(X), y)  # 计算损失
            l.backward()  # 反向传播计算梯度
            optimizer.step()  # 更新参数
        train_ls.append(log_rmes(net, train_features, train_labels))
        if test_labels is not None:
            test_ls.append(log_rmes(net, test_features, test_labels))
    return train_ls, test_ls


# K折交叉验证
def get_k_fold_data(k, i, X, y):
    assert k > 1
    fold_size = X.shape[0] // k
    X_train, y_train = None, None
    for j in range(k):
        idx = slice(j * fold_size, (j + 1) * fold_size)  # 创建一个切片对象
        X_part, y_part = X[idx, :], y[idx]  # 将切片对象应用于索引
        if j == i:  # 取出第i份作为验证集
            X_valid, y_valid = X_part, y_part
        elif X_train is None:  # 如果当前训练集没有数据就初始化
            X_train, y_train = X_part, y_part
        else:
            X_train = torch.cat([X_train, X_part], 0)  # 如果是训练集那么就进行合并
            y_train = torch.cat([y_train, y_part], 0)
    return X_train, y_train, X_valid, y_valid


# k次的k折交叉验证
def k_fold(k, X_train, y_train, num_epochs, learning_rate, weight_decay, batch_size):
    train_l_sum, valid_l_sum = 0, 0
    for i in range(k):
        data = get_k_fold_data(k, i, X_train, y_train)
        net = get_net()
        train_ls, valid_ls = train(net, *data, num_epochs, learning_rate, weight_decay, batch_size)
        train_l_sum += train_ls[-1]
        valid_l_sum += valid_ls[-1]
        if i == 0:
            d2l.plot(list(range(1, num_epochs + 1)), [train_ls, valid_ls], xlabel="epoch",
                     ylabel='ylabel', xlim=[1, num_epochs], legend=["train", 'valid'], yscale='log')
        print(f"折{i + 1},训练log rmse{float(train_ls[-1]):f},"
              f"验证log rmse{float(valid_ls[-1]):f}")
    return train_l_sum / k, valid_l_sum / k


k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
train_l,valid_l = k_fold(k,train_features, train_labels, num_epochs, lr, weight_decay, batch_size)
print(f"{k}折验证：平均训练log rmse:{float(train_l):f}",
      f"平均验证log rmse:{float(valid_l):f}")
plt.show()

下面为我自己调试的结果：

def get_net():
    net = nn.Sequential(nn.Linear(in_features, 256),
                        nn.ReLU(),
                        nn.Linear(256,1))
    return net
k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
5折验证：平均训练log rmse:0.045112 平均验证log rmse:0.157140

我总感觉256直接到1不太好，因此调整了模型的结构：

def get_net():
    net = nn.Sequential(nn.Linear(in_features, 128),
                        nn.ReLU(),
                        nn.Linear(128,1))
    return net
k, num_epochs, lr, weight_decay, batch_size = 5, 100, 0.03, 1, 64
5折验证：平均训练log rmse:0.109637 平均验证log rmse:0.136201

更复杂的模型总感觉没办法再降低误差了。