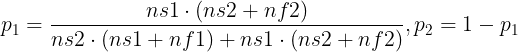Self-adaptive Differential Evolution Algorithm for Numerical Optimization

0、论文背景

本文在DE算法的基础上，提出了一种自适应的差分进化算法(SaDE)。其中学习策略的选择和两个控制参数F和CR不需要预先指定。

Qin A K, Suganthan P N. Self-adaptive differential evolution algorithm for numerical optimization[C]//2005 IEEE congress on evolutionary computation. IEEE, 2005, 2: 1785-1791.

1、SaDE

DE算法相关知识参见博客：DE 。

1.1 learning strategy

这里主要针对突变操作采用了两个策略：

上述两个策略侧重点不一样，其中，策略1通常表现出良好的多样性，而策略2则表现出良好的收敛性， 为了平衡全局搜索和局部搜索，本文采用两种方式组合的方式。

该策略的思路：

• 首先初始化两个策略被采用的概率，p1 = 0.5，p2 = 0.5，ns1 = 0，ns2 = 0，nf1 = 0，nf2 = 0。
• rand()函数随机产生一个数，小于p1，采用策略1对该个体进行突变操作；否则，采用策略2。
• 在选择操作完成后，运用策略1产生的突变个体保留了下来，ns1加1，没有保留下来，nf1加1；运用策略2产生的突变个体保留了下来，ns2加1，没有保留下来，nf2加1。
• 算法迭代50次后，更新p1和p2；同时重置：ns1 = 0，ns2 = 0，nf1 = 0，nf2 = 0。

1.2 自适应F值

F值设置需要有一个较大的灵活性，因为F值与收敛性有关，F值越大，种群多样性越好；F值越小收敛性越好。在这里F值是采用正态分布随机生成的：

1.3 自适应CR值

良好的CR参数值通常在较小的范围内，因此，我们考虑在一定的生成间隔内积累以往的学习经验，从而动态调整CR值到一个合适的范围。CR值的产生也是采用正态分布随机产生的：

该策略的思路：

• 首先初始化CRm参数，CRm = 0.5。
• 然后根据正态分布产生每个个体交叉过程中的CR。
• 在选择过程完成后，记录选择后的个体的CR值。
• 在迭代5次之后，将CRm更新为记录的CR值的均值，同时清空记录的CR值。

2、算法的实现以及简单实验

DE和NSDE相关实现在博客中有展示：NSDE

function [globalBest, globalBestFitness, FitnessHistory] = SaDE(popsize, maxIteration,dim, LB, UB, Fun)
% 种群的初始化和计算适应度值
Sol(popsize, dim) = 0; % Declare memory.
Fitness(popsize) = 0;
for i = 1:popsize
    Sol(i,:) = LB+(UB-LB).* rand(1, dim);
    Fitness(i) = Fun(Sol(i,:));
end

% 获得全局最优值以及对应的种群向量
[fbest, bestIndex] = min(Fitness);
globalBest = Sol(bestIndex,:);
globalBestFitness = fbest;

% 策略学习初始化值的设置
p1 = 0.5;
ns1 = 0;
ns2 = 0;
nf1 = 0;
nf2 = 0;
CRm = 0.5;
CRRecord = [];

% 开始迭代
for time = 1:maxIteration
    for i = 1:popsize
        % 突变
        F = normrnd(0.5,0.3);  %正太分布随机数
        if F < 0
            F = 0.0001;
        elseif F > 2
            F = 2;
        end
        if rand() <= p1
            r = randperm(popsize, 3);   %策略1
            mutantPos = Sol(r(1),:) + F * (Sol(r(2),:) - Sol(r(3),:));%在1~pop中随机选择3个数组成一个数组
            tag = 1;
        else
            r = randperm(popsize, 2);   %策略2
            mutantPos = Sol(i,:) + F * (globalBest - Sol(i,:)) + F * (Sol(r(1),:) - Sol(r(2),:));
            tag = 2;
        end

        % 交叉
        jj = randi(dim);  % 选择至少一维发生交叉
        CR = normrnd(CRm,0.1); 
        for d = 1:dim
            if rand() < CR || d == jj
                crossoverPos(d) = mutantPos(d);
            else
                crossoverPos(d) = Sol(i,d);
            end
        end

        % 检查是否越界.
        crossoverPos(crossoverPos>UB) = UB(crossoverPos>UB);
        crossoverPos(crossoverPos

clear;clc;clearvars;
% 初始化变量维度,种群数,最大迭代次数,搜索区间,F,CR
dim = 20;
popsize = 100;
maxIteration = 1000;
LB = -5.12 * ones(1, dim);
UB = 5.12 * ones(1, dim);
F = 1;
CR = 0.9;
[globalBest, globalBestFitness, FitnessHistory] = DE(popsize, maxIteration,dim, LB, UB, F, CR, @(x)Griewank(x));
[globalBest1, globalBestFitness1, FitnessHistory1] = NSDE(popsize, maxIteration,dim, LB, UB, CR, @(x)Griewank(x));
[globalBest2, globalBestFitness2, FitnessHistory2] = SaDE(popsize, maxIteration,dim, LB, UB, @(x)Griewank(x));
plot(FitnessHistory);
hold on;
plot(FitnessHistory1);
hold on;
plot(FitnessHistory2);
legend('DE','NSDE','SaDE','Location', 'northeast');

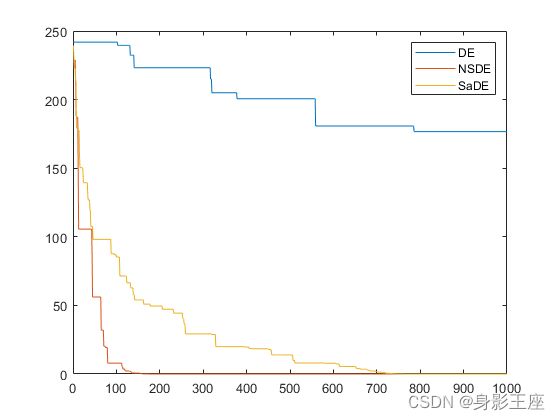
Griewank函数测试结果：

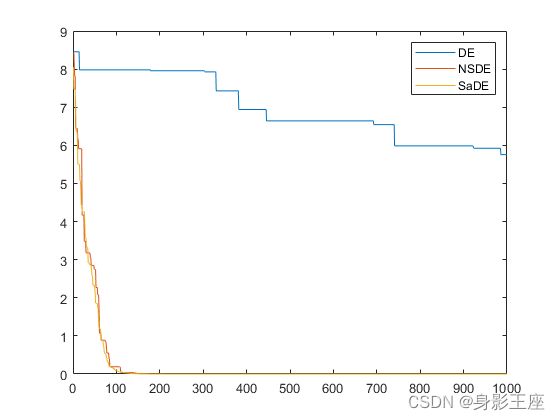
 Rastrigin函数测试结果：

Ackley 函数测试结果：

可以看出SaDE和NSDE在性能上均比DE有不小的提升，可以看出自适应参数确实在搜索和收敛上有非常大的帮助。

如有错误，还望批评指正！