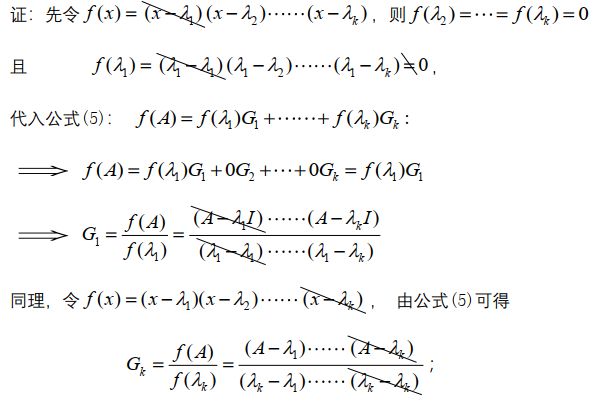【矩阵论】2. 矩阵分解——正规分解
矩阵论
1. 准备知识——复数域上的矩阵与换位公式)
1. 准备知识——复数域上的内积域正交阵
1. 准备知识——相似对角化与合同&正定阵
2. 矩阵分解—— SVD准备知识——奇异值
2. 矩阵分解——SVD
2. 矩阵分解——QR分解
2. 矩阵分解——乔利斯分解&平方根公式
2. 矩阵分解——正规谱分解——正规阵
2. 矩阵分解——正规分解
2. 矩阵分解——单阵及特征值特征向量一些求法
6.2 正规分解定理
若 A = A n × n A=A_{n\times n} A=An×n 正规,则存在U阵Q,使 Q H A Q = Λ = ( λ 1 ⋱ λ n ) Q^HAQ=\Lambda=\left(\begin{matrix}\lambda_1&&\\&\ddots&\\&&\lambda_n\end{matrix}\right) QHAQ=Λ=⎝ ⎛λ1⋱λn⎠ ⎞
证明
设 A = A n × n 正规,由 U 相似定理, Q H A Q 正规,由许尔公式,存在 U 阵 Q ,使 Q H A Q = D = ( λ 1 ∗ ⋱ λ n ) 为上三角阵 D = Q H A Q 为正规三角阵,由 " 正规三角定理 " 可知 D 为对角阵 即 Q − 1 A Q = D = ( λ 1 ⋱ λ n ) 成立 \begin{aligned} &设A=A_{n\times n} 正规,由U相似定理,Q^HAQ正规,由许尔公式,存在U阵Q,使\\ &Q^HAQ=D=\left( \begin{matrix} \lambda_1&&*\\ &\ddots&\\ &&\lambda_n \end{matrix} \right)为上三角阵\\ &D=Q^HAQ为正规三角阵,由 "正规三角定理" 可知D为对角阵\\ &即Q^{-1}AQ=D=\left( \begin{matrix} \lambda_1&&\\ &\ddots&\\ &&\lambda_n \end{matrix} \right)成立 \end{aligned} 设A=An×n正规,由U相似定理,QHAQ正规,由许尔公式,存在U阵Q,使QHAQ=D=⎝ ⎛λ1⋱∗λn⎠ ⎞为上三角阵D=QHAQ为正规三角阵,由"正规三角定理"可知D为对角阵即Q−1AQ=D=⎝ ⎛λ1⋱λn⎠ ⎞成立
6.2.1 正规阵A恰有n个正交特向
由 Q − 1 A Q = D = ( λ 1 ⋱ λ n ) ⇒ A Q = Q D ⇒ A ( q 1 , ⋯ , q n ) = ( q 1 , ⋯ , q n ) D ⇒ ( A q 1 , ⋯ , A q n ) = ( λ 1 q 1 , ⋯ , λ n q n ) U 阵 Q 为 A 的特征向量组成的矩阵,且 n 个特征向量相互正交, q 1 ⊥ ⋯ ⊥ q n \begin{aligned} &由Q^{-1} AQ=D=\left( \begin{matrix} \lambda_1&&\\ &\ddots&\\ &&\lambda_n \end{matrix} \right)\Rightarrow AQ=QD\\&\Rightarrow A\left(q_1,\cdots,q_n\right)=\left(q_1,\cdots,q_n\right)D\\ &\Rightarrow\left(Aq_1,\cdots,Aq_n\right)=\left(\lambda_1q_1,\cdots,\lambda_nq_n\right)\\ &U阵Q为A的特征向量组成的矩阵,且n个特征向量相互正交,q_1\bot \cdots \bot q_n \end{aligned} 由Q−1AQ=D=⎝ ⎛λ1⋱λn⎠ ⎞⇒AQ=QD⇒A(q1,⋯,qn)=(q1,⋯,qn)D⇒(Aq1,⋯,Aqn)=(λ1q1,⋯,λnqn)U阵Q为A的特征向量组成的矩阵,且n个特征向量相互正交,q1⊥⋯⊥qn
6.2.2 正规分解方法
-
先令特征根 λ 1 , ⋯ , λ n \lambda_1,\cdots,\lambda_n λ1,⋯,λn ,求正交特征向量 X 1 ⊥ ⋯ ⊥ X n X_1\bot \cdots \bot X_n X1⊥⋯⊥Xn
-
令U阵 Q = ( q 1 , ⋯ , q n ) = ( X 1 ∣ X 1 ∣ , ⋯ , X n ∣ X n ∣ ) Q=\left(q_1,\cdots,q_n\right)=\left(\frac{X_1}{\vert X_1\vert},\cdots,\frac{X_n}{\vert X_n \vert}\right) Q=(q1,⋯,qn)=(∣X1∣X1,⋯,∣Xn∣Xn)
则有U相似阵 Q H A Q = D = ( λ 1 ⋱ λ n ) Q^HAQ=D=\left(\begin{matrix}\lambda_1&&\\&\ddots&\\&&\lambda_n\end{matrix}\right) QHAQ=D=⎝ ⎛λ1⋱λn⎠ ⎞ 为对角阵
-
可写正规分解 A = Q D Q H A=QDQ^H A=QDQH
定义法
对矩阵 A = ( 1 − 1 1 0 ) A=\left(\begin{matrix} 1&-1\\1&0\end{matrix}\right) A=(11−10) 正规分解
A = ( 1 − 1 1 0 ) 为正规阵,计算可得 λ 1 = i , λ 2 = − i , X 1 = ( i 1 ) , X 2 = ( 1 i ) , 且 X 1 与 X 2 为不同特征值的特征向量,所以 X 1 ⊥ X 2 令 U 阵 Q = ( X 1 ∣ X 1 ∣ , X 2 ∣ X 2 ∣ ) = 1 2 ( i 1 1 i ) , 可得 Q H A Q = D = ( i − i ) 则有正规分解 A = Q D Q H = 1 2 ( i 1 1 i ) ( i − i ) 1 2 ( − i 1 1 − i ) \begin{aligned} &A=\left( \begin{matrix} 1&-1\\ 1&0 \end{matrix} \right)为正规阵,计算可得\lambda_1=i,\lambda_2=-i,X_1=\left( \begin{matrix} i\\1 \end{matrix} \right),X_2=\left( \begin{matrix} 1\\i \end{matrix} \right),\\ &且X_1与X_2为不同特征值的特征向量,所以X_1\bot X_2\\ &令U阵Q=\left( \begin{matrix} \frac{X_1}{\vert X_1\vert},\frac{X_2}{\vert X_2\vert} \end{matrix} \right)=\frac{1}{\sqrt{2}}\left( \begin{matrix} i&1\\ 1&i \end{matrix} \right),可得Q^HAQ=D=\left( \begin{matrix} i&\\ &-i \end{matrix} \right)\\ &则有正规分解 A=QDQ^H=\frac{1}{\sqrt{2}}\left( \begin{matrix} i&1\\ 1&i \end{matrix} \right)\left( \begin{matrix} i&\\ &-i \end{matrix} \right)\frac{1}{\sqrt{2}}\left( \begin{matrix} -i&1\\ 1&-i \end{matrix} \right) \end{aligned} A=(11−10)为正规阵,计算可得λ1=i,λ2=−i,X1=(i1),X2=(1i),且X1与X2为不同特征值的特征向量,所以X1⊥X2令U阵Q=(∣X1∣X1,∣X2∣X2)=21(i11i),可得QHAQ=D=(i−i)则有正规分解A=QDQH=21(i11i)(i−i)21(−i11−i)
平移法
令 B = ( 1 − 1 1 1 ) = I + A = ( 1 1 ) + ( 0 − 1 1 0 ) , 其中 A 为正规 U 阵 λ ( B ) = { λ 1 , λ 2 } = { 1 + i , 1 − i } , X 1 = ( i 1 ) , X 2 = ( 1 i ) , 得 U 阵 Q = ( X 1 ∣ X 1 ∣ , X 2 ∣ X 2 ∣ ) = 1 2 ( i 1 1 i ) ,故有正规分解 A = Q D Q H = 1 2 ( i 1 1 i ) ( 1 + i 1 − i ) 1 2 ( − i 1 1 − i ) \begin{aligned} &令B=\left( \begin{matrix} 1&-1\\ 1&1 \end{matrix} \right)=I+A=\left( \begin{matrix} 1&\\ &1 \end{matrix} \right)+\left( \begin{matrix} 0&-1\\ 1&0 \end{matrix} \right),其中A为正规U阵\\ &\lambda(B)=\{\lambda_1,\lambda_2\}=\{1+i,1-i\},X_1=\left( \begin{matrix} i\\1 \end{matrix} \right),X_2=\left( \begin{matrix} 1\\i \end{matrix} \right),\\ &得U阵Q=\left(\frac{X_1}{\vert X_1\vert},\frac{X_2}{\vert X_2\vert}\right)=\frac{1}{\sqrt{2}}\left( \begin{matrix} i&1\\ 1&i \end{matrix} \right),故有正规分解A=QDQ^H\\ &=\frac{1}{\sqrt{2}}\left( \begin{matrix} i&1\\ 1&i \end{matrix} \right)\left( \begin{matrix} 1+i&\\ &1-i \end{matrix} \right)\frac{1}{\sqrt{2}}\left( \begin{matrix} -i&1\\ 1&-i \end{matrix} \right) \end{aligned} 令B=(11−11)=I+A=(11)+(01−10),其中A为正规U阵λ(B)={λ1,λ2}={1+i,1−i},X1=(i1),X2=(1i),得U阵Q=(∣X1∣X1,∣X2∣X2)=21(i11i),故有正规分解A=QDQH=21(i11i)(1+i1−i)21(−i11−i)
6.3 正规谱分解
6.3.1 正规分解推导
若 A = A n × n 正规,互异根为 λ 1 , ⋯ , λ k ,则有 Q H A Q = D = ( λ 1 I 1 ⋱ λ k I k ) 其中 Q 为 U 阵, Q H = Q − 1 , I 1 , ⋯ , I k 为单位阵 ( 如 D = ( 2 ( 1 1 ) 3 ( 1 1 ) ) = ( 2 I 1 3 I 2 ) ) 可设 Q − 1 A Q = D = ( λ 1 I 1 0 ⋱ 0 λ k I k ) ( Q 为 U 阵, Q H = Q − 1 ) 写为 D = λ 1 ( I 1 0 ⋱ 0 0 ) + λ 2 ( 0 0 I 2 0 ⋱ ) + ⋯ + λ k ( 0 0 ⋱ 0 I k ) 则令 D 1 = ( I 1 0 ⋱ 0 0 ) , D 2 = ( 0 0 I 2 0 ⋱ ) , ⋯ , D k = ( 0 0 ⋱ 0 I k ) ⇒ Q − 1 A Q = D = λ 1 D 1 + λ 2 D 2 + ⋯ + λ k D k \begin{aligned} &若A=A_{n\times n} 正规,互异根为 \lambda_1,\cdots,\lambda_k,则有Q^HAQ=D=\left( \begin{matrix} \lambda_1I_1&&\\ &\ddots&\\ &&\lambda_kI_k \end{matrix} \right)\\ &其中Q为U阵,Q^H=Q^{-1},I_1,\cdots,I_k为单位阵\\ &\left(如D=\left( \begin{matrix} 2\left( \begin{matrix} 1&\\ &1 \end{matrix} \right)\\ &3\left( \begin{matrix} 1&\\ &1 \end{matrix} \right) \end{matrix} \right)=\left( \begin{matrix} 2I_1&\\ &3I_2 \end{matrix} \right)\right)\\ &可设 Q^{-1}AQ=D=\left( \begin{matrix} \lambda_1I_1&&0\\ &\ddots&\\ 0&&\lambda_kI_k \end{matrix} \right)(Q为U阵,Q^H=Q^{-1})\\ &写为D=\lambda_1\left( \begin{matrix} I_1&&0\\ &\ddots&\\ 0&&0 \end{matrix} \right)+\lambda_2\left( \begin{matrix} 0&&0\\ &I_2&\\ 0&&\ddots \end{matrix} \right)+\cdots+\lambda_k\left( \begin{matrix} 0&&0\\ &\ddots&\\ 0&&I_k \end{matrix} \right)\\ &则令D_1=\left( \begin{matrix} I_1&&0\\ &\ddots&\\ 0&&0 \end{matrix} \right),D_2=\left( \begin{matrix} 0&&0\\ &I_2&\\ 0&&\ddots \end{matrix} \right),\cdots,D_k=\left( \begin{matrix} 0&&0\\ &\ddots&\\ 0&&I_k \end{matrix} \right)\\ &\Rightarrow Q^{-1}AQ=D=\lambda_1D_1+\lambda_2D_2+\cdots+\lambda_kD_k\\ \end{aligned} 若A=An×n正规,互异根为λ1,⋯,λk,则有QHAQ=D=⎝ ⎛λ1I1⋱λkIk⎠ ⎞其中Q为U阵,QH=Q−1,I1,⋯,Ik为单位阵⎝ ⎛如D=⎝ ⎛2(11)3(11)⎠ ⎞=(2I13I2)⎠ ⎞可设Q−1AQ=D=⎝ ⎛λ1I10⋱0λkIk⎠ ⎞(Q为U阵,QH=Q−1)写为D=λ1⎝ ⎛I10⋱00⎠ ⎞+λ2⎝ ⎛00I20⋱⎠ ⎞+⋯+λk⎝ ⎛00⋱0Ik⎠ ⎞则令D1=⎝ ⎛I10⋱00⎠ ⎞,D2=⎝ ⎛00I20⋱⎠ ⎞,⋯,Dk=⎝ ⎛00⋱0Ik⎠ ⎞⇒Q−1AQ=D=λ1D1+λ2D2+⋯+λkDk
则可得出结论:
①和为单位阵: D 1 + D 2 + ⋯ + D k = ( I 1 ⋱ I k ) = I ( 单位阵 ) , ②正交: D 1 D 2 = 0 , ⋯ , D i D j = 0 ( i ≠ j ) ③幂等: D 1 2 = D 1 , ⋯ , D k 2 = D k ,且 D 1 H = D 1 , ⋯ , D k H = D k \begin{aligned} &①和为单位阵:D_1+D_2+\cdots+D_k=\left( \begin{matrix} I_1&&\\ &\ddots&\\ &&I_k \end{matrix} \right)=I(单位阵),\\ &②正交:D_1D_2=0,\cdots,D_iD_j=0(i\neq j)\\ &③幂等:D_1^2=D_1,\cdots,D_k^2=D_k,且D_1^H=D_1,\cdots,D_k^H=D_k\\ \end{aligned} ①和为单位阵:D1+D2+⋯+Dk=⎝ ⎛I1⋱Ik⎠ ⎞=I(单位阵),②正交:D1D2=0,⋯,DiDj=0(i=j)③幂等:D12=D1,⋯,Dk2=Dk,且D1H=D1,⋯,DkH=Dk
故可等价写为:
Q H A Q = D = λ 1 D 1 + λ 2 D 2 + ⋯ + λ k D k ⇒ A = Q D Q H = λ 1 Q D 1 Q H + λ 2 Q D 2 Q H + ⋯ + λ k Q D k Q H 可令 G 1 = Q D 1 Q H , ⋯ , G k = Q D k Q H ⇒ A = λ 1 G 1 + ⋯ + λ k G k \begin{aligned} &Q^HAQ=D=\lambda_1D_1+\lambda_2D_2+\cdots+\lambda_kD_k\\ &\Rightarrow A=QDQ^H=\lambda_1QD_1Q^H+\lambda_2QD_2Q^H+\cdots+\lambda_kQD_kQ^H\\ &可令G_1=QD_1Q^H,\cdots,G_k=QD_kQ^H\\ &\Rightarrow A=\lambda_1G_1+\cdots+\lambda_kG_k \end{aligned} QHAQ=D=λ1D1+λ2D2+⋯+λkDk⇒A=QDQH=λ1QD1QH+λ2QD2QH+⋯+λkQDkQH可令G1=QD1QH,⋯,Gk=QDkQH⇒A=λ1G1+⋯+λkGk
有类似推论:
① G 1 + G 2 + ⋯ + G k = I ∵ G 1 + G 2 + ⋯ + G k = Q ( D 1 Q − 1 + D 2 + ⋯ + D k ) Q − 1 = Q I Q − 1 = I ② G 1 G 2 = 0 , ⋯ , G i G j = 0 ( i ≠ j ) ∵ G 1 G 2 = ( Q D 1 Q − 1 ) ( Q D 2 Q − 1 ) = 0 ③ G 1 2 = G 1 , ⋯ , G k 2 = G k , 且 G 1 H = G 1 , ⋯ , G k H = G k 都是 H e r m i t e 阵 \begin{aligned} &①G_1+G_2+\cdots+G_k=I\\ &\quad \because G_1+G_2+\cdots+G_k=Q(D_1Q^{-1}+D_2+\cdots+D_k)Q^{-1}=QIQ^{-1}=I \\ &②G_1G_2=0,\cdots,G_iG_j=0(i \neq j)\\ &\quad \because G_1G_2=(QD_1Q^{-1})(QD_2Q^{-1})=0\\ &③G_1^2=G_1,\cdots,G_k^2=G_k,且G_1^H=G_1,\cdots,G_k^H=G_k都是Hermite阵 \end{aligned} ①G1+G2+⋯+Gk=I∵G1+G2+⋯+Gk=Q(D1Q−1+D2+⋯+Dk)Q−1=QIQ−1=I②G1G2=0,⋯,GiGj=0(i=j)∵G1G2=(QD1Q−1)(QD2Q−1)=0③G12=G1,⋯,Gk2=Gk,且G1H=G1,⋯,GkH=Gk都是Hermite阵
6.3.2 正规阵谱分解与谱阵性质
若 A = A n × n 正规,全体互异根为 λ 1 , ⋯ , λ k ,则有 A = λ 1 G 1 + λ 2 G 2 + ⋯ + λ k G k 其中 G 1 , ⋯ , G k 为 A 的谱阵 \begin{aligned} &若A=A_{n\times n} 正规,全体互异根为 \lambda_1,\cdots,\lambda_k,则有A=\lambda_1G_1+\lambda_2G_2+\cdots+\lambda_kG_k\\ &其中G_1,\cdots,G_k为A的谱阵 \end{aligned} 若A=An×n正规,全体互异根为λ1,⋯,λk,则有A=λ1G1+λ2G2+⋯+λkGk其中G1,⋯,Gk为A的谱阵
性质
①和为 I : G 1 + G 2 + ⋯ + G k = I ②正交: G 1 G 2 = 0 , ⋯ , G i G j = 0 ( i ≠ j ) ③幂等: G 1 2 = G 1 , ⋯ , G k 2 = G k ( 幂等 ) , 且 G 1 H = G 1 , ⋯ , G k H = G k ④正规阵幂次: A p = λ 1 p G 1 + ⋯ + λ k G k , p = 0 , 1 , 2. ⋯ ⑤正规阵函数: f ( A ) = f ( λ 1 ) G 1 + ⋯ + f ( λ k ) G k , f ( x ) = c 0 + c 1 x 1 + ⋯ + c p x p ∵ f ( A ) = c 0 I + c 1 A + ⋯ + c k A p = c 0 ( G 1 + ⋯ + G k ) + c 1 ( λ 1 G 1 + λ 2 G 2 + ⋯ + λ k G k ) + ⋯ + c p ( λ 1 p G 1 + λ 2 p G 2 + ⋯ + λ p k G k ) = ( c 0 + c 1 λ 1 + c p λ 1 k ) G 1 + ( c 0 + c 1 λ 2 + ⋯ + c p λ 2 p k ) G 2 + ⋯ + ( c 0 + c 1 λ k + ⋯ + c p λ k p ) G k = f ( λ 1 ) G 1 + ⋯ + f ( λ k ) G k ⑥正规阵求法:设 A 正规,全体不同根为 λ 1 , λ 2 , ⋯ , λ k ,则有谱阵公式 G 1 , G 2 , ⋯ , G k G 1 = ( A − λ 2 I ) ⋯ ( A − λ k I ) ( λ 1 − λ 2 ) ⋯ ( λ 1 − λ k ) , G 1 = ( A − λ 1 I ) ( A − λ 3 I ) ⋯ ( A − λ k I ) ( λ 2 − λ 1 ) ( λ 2 − λ 3 ) ⋯ ( λ 2 − λ k ) ⋯ G k = ( A − λ 1 I ) ( A − λ 2 I ) ⋯ ( A − λ k − 1 I ) ( λ k − λ 1 ) ( λ k − λ 2 ) ⋯ ( λ k − λ k − 1 ) ⑦谱阵中列是 A 的特征向量: A G 1 = λ 1 G 1 , A G 2 = λ 2 G 2 , ⋯ , A G k = λ k G k ∵ A G 1 = ( λ 1 G 1 + ⋯ + λ k G k ) G 1 = λ 1 G 1 \begin{aligned} &①和为I:G_1+G_2+\cdots+G_k=I\\ &②正交:G_1G_2=0,\cdots,G_iG_j=0(i\neq j)\\ &③幂等: G_1^{2}=G_1,\cdots,G_k^{2}=G_k(幂等),且G_1^H=G_1,\cdots ,G_k^H=G_k\\ &④正规阵幂次:A^p=\lambda_1^pG_1+\cdots+\lambda_kG_k,p=0,1,2.\cdots\\ &⑤正规阵函数:f(A)=f(\lambda_1)G_1+\cdots+f(\lambda_k)G_k,f(x)=c_0+c_1x_1+\cdots+c_px^p\\ & \quad \because f(A)=c_0I+c_1A+\cdots+c_kA^p\\ & \quad \quad =c_0(G_1+\cdots+G_k)+c_1(\lambda_1G_1+\lambda_2G_2+\cdots+\lambda_kG_k)+\\ & \quad \quad \quad \cdots+c_p(\lambda_1^pG_1+\lambda_2^pG_2+\cdots+\lambda_p^kG_k)\\ & \quad \quad =(c_0+c_1\lambda_1+c_p\lambda_1^k)G_1+(c_0+c_1\lambda_2+\cdots+c_p\lambda_2^pk)G_2+\\ & \quad \quad \quad \cdots+(c_0+c_1\lambda_k+\cdots+c_p\lambda_k^p)G_k\\ & \quad \quad =f(\lambda_1)G_1+\cdots+f(\lambda_k)G_k\\ &⑥正规阵求法:设A正规,全体不同根为 \lambda_1,\lambda_2,\cdots,\lambda_k,则有谱阵公式G_1,G_2,\cdots,G_k\\ &\quad G_1=\frac{(A-\lambda_2I)\cdots(A-\lambda_kI)}{(\lambda_1-\lambda_2)\cdots(\lambda_1-\lambda_k)},G_1=\frac{(A-\lambda_1I)(A-\lambda_3I)\cdots(A-\lambda_kI)}{(\lambda_2-\lambda_1)(\lambda_2-\lambda_3)\cdots(\lambda_2-\lambda_k)}\\ &\quad\cdots\\ &\quad G_k=\frac{(A-\lambda_1I)(A-\lambda_2I)\cdots(A-\lambda_{k-1}I)}{(\lambda_k-\lambda_1)(\lambda_k-\lambda_2)\cdots(\lambda_k-\lambda_{k-1})}\\ &⑦谱阵中列是A的特征向量:AG_1=\lambda_1G_1,AG_2=\lambda_2G_2,\cdots,AG_k=\lambda_kG_k\\ &\quad \because AG_1=(\lambda_1G_1+\cdots+\lambda_kG_k)G_1=\lambda_1G_1 \end{aligned} ①和为I:G1+G2+⋯+Gk=I②正交:G1G2=0,⋯,GiGj=0(i=j)③幂等:G12=G1,⋯,Gk2=Gk(幂等),且G1H=G1,⋯,GkH=Gk④正规阵幂次:Ap=λ1pG1+⋯+λkGk,p=0,1,2.⋯⑤正规阵函数:f(A)=f(λ1)G1+⋯+f(λk)Gk,f(x)=c0+c1x1+⋯+cpxp∵f(A)=c0I+c1A+⋯+ckAp=c0(G1+⋯+Gk)+c1(λ1G1+λ2G2+⋯+λkGk)+⋯+cp(λ1pG1+λ2pG2+⋯+λpkGk)=(c0+c1λ1+cpλ1k)G1+(c0+c1λ2+⋯+cpλ2pk)G2+⋯+(c0+c1λk+⋯+cpλkp)Gk=f(λ1)G1+⋯+f(λk)Gk⑥正规阵求法:设A正规,全体不同根为λ1,λ2,⋯,λk,则有谱阵公式G1,G2,⋯,GkG1=(λ1−λ2)⋯(λ1−λk)(A−λ2I)⋯(A−λkI),G1=(λ2−λ1)(λ2−λ3)⋯(λ2−λk)(A−λ1I)(A−λ3I)⋯(A−λkI)⋯Gk=(λk−λ1)(λk−λ2)⋯(λk−λk−1)(A−λ1I)(A−λ2I)⋯(A−λk−1I)⑦谱阵中列是A的特征向量:AG1=λ1G1,AG2=λ2G2,⋯,AGk=λkGk∵AG1=(λ1G1+⋯+λkGk)G1=λ1G1
谱阵求法
由推论⑤可知,取k个不同的函数f(x)可求出谱阵 G 1 , G 2 , ⋯ . G k G_1,G_2,\cdots.G_k G1,G2,⋯.Gk
证明:
A正规有2个不同根
G 1 = A − λ 2 I λ 1 − λ 2 , G 2 = I − G 1 = A − λ 1 I λ 2 − λ 1 \begin{aligned} G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2},G_2=I-G_1=\frac{A-\lambda_1I}{\lambda_2-\lambda_1} \end{aligned} G1=λ1−λ2A−λ2I,G2=I−G1=λ2−λ1A−λ1I
A正规且有3个不同根
G 1 = ( A − λ 2 I ) ( A − λ 3 I ) ( λ 1 − λ 2 ) ( λ 1 − λ 3 ) , G 2 = ( A − λ 1 I ) ( A − λ 3 I ) ( λ 2 − λ 1 ) ( λ 2 − λ 3 ) , G 3 = I − G 1 − G 2 = ( A − λ 1 I ) ( A − λ 2 I ) ( λ 3 − λ 1 ) ( λ 3 − λ 2 ) \begin{aligned} &G_1=\frac{(A-\lambda_2I)(A-\lambda_3I)}{(\lambda_1-\lambda_2)(\lambda_1-\lambda_3)},G_2=\frac{(A-\lambda_1I)(A-\lambda_3I)}{(\lambda_2-\lambda_1)(\lambda_2-\lambda_3)},\\ &G_3=I-G_1-G_2=\frac{(A-\lambda_1I)(A-\lambda_2I)}{(\lambda_3-\lambda_1)(\lambda_3-\lambda_2)} \end{aligned} G1=(λ1−λ2)(λ1−λ3)(A−λ2I)(A−λ3I),G2=(λ2−λ1)(λ2−λ3)(A−λ1I)(A−λ3I),G3=I−G1−G2=(λ3−λ1)(λ3−λ2)(A−λ1I)(A−λ2I)
正规分解性质的应用例
1
A = ( 1 0 − 2 0 0 0 − 2 0 4 ) ( 实对称正规阵 ) ,求 A 与 f ( A ) 的谱分解,与 A 100 \begin{aligned} A=\left( \begin{matrix} 1&0&-2\\ 0&0&0\\ -2&0&4 \end{matrix} \right)(实对称正规阵),求A与f(A)的谱分解,与A^{100} \end{aligned} A=⎝ ⎛10−2000−204⎠ ⎞(实对称正规阵),求A与f(A)的谱分解,与A100
可知 A 为秩 1 矩阵, r ( A ) = 1 , 特征根为 λ ( A ) = 5 , 0 , 0 , 不同根为 λ 1 = 5 , λ 2 = 0 G 1 = A − λ 2 I λ 1 − λ 2 = 1 5 ( 1 0 − 2 0 0 0 − 2 0 4 ) , G 2 = A − λ 1 I λ 2 − λ 1 = I − G 1 = 1 5 ( 4 0 2 0 5 0 2 0 1 ) 得谱分解: A = λ 1 G 1 + λ 2 G 2 , 且 f ( A ) = f ( λ 1 ) G 1 + f ( λ 2 ) G 2 即 f ( A ) = f ( 5 ) G 1 + f ( 0 ) G 2 令 f ( x ) = x 100 ⇒ A 100 = f ( 5 ) G 1 + f ( 0 ) G 2 = 5 100 G 1 = 5 100 1 5 A = 5 99 A 由于 G 中列向量都是 A 的特征向量,所以 λ 1 = 5 的特征向量 α 1 = ( 1 0 − 2 ) λ 2 = 0 的特征向量 α 2 = ( 2 0 1 ) , α 3 = ( 0 1 0 ) \begin{aligned} &可知A为秩1矩阵,r(A)=1,特征根为\lambda(A)={5,0,0},不同根为\lambda_1=5,\lambda_2=0\\ &G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2}=\frac{1}{5}\left( \begin{matrix} 1&0&-2\\ 0&0&0\\ -2&0&4 \end{matrix} \right),G_2=\frac{A-\lambda_1I}{\lambda_2-\lambda_1}=I-G_1=\frac{1}{5}\left( \begin{matrix} 4&0&2\\ 0&5&0\\ 2&0&1 \end{matrix} \right)\\ &得谱分解:A=\lambda_1G_1+\lambda_2G_2,且f(A)=f(\lambda_1)G_1+f(\lambda_2)G_2\\ &即f(A)=f(5)G_1+f(0)G_2\\ &令f(x)=x^{100}\Rightarrow A^{100}=f(5)G_1+f(0)G_2=5^{100}G_1=5^{100}\frac{1}{5}A=5^{99}A\\ &由于G中列向量都是A的特征向量,所以\lambda_1=5的特征向量\alpha_1=\left( \begin{matrix} 1\\0\\-2 \end{matrix} \right)\\ &\lambda_2=0的特征向量\alpha_2=\left( \begin{matrix} 2\\0\\1 \end{matrix} \right),\alpha_3=\left( \begin{matrix} 0\\1\\0 \end{matrix} \right) \end{aligned} 可知A为秩1矩阵,r(A)=1,特征根为λ(A)=5,0,0,不同根为λ1=5,λ2=0G1=λ1−λ2A−λ2I=51⎝ ⎛10−2000−204⎠ ⎞,G2=λ2−λ1A−λ1I=I−G1=51⎝ ⎛402050201⎠ ⎞得谱分解:A=λ1G1+λ2G2,且f(A)=f(λ1)G1+f(λ2)G2即f(A)=f(5)G1+f(0)G2令f(x)=x100⇒A100=f(5)G1+f(0)G2=5100G1=510051A=599A由于G中列向量都是A的特征向量,所以λ1=5的特征向量α1=⎝ ⎛10−2⎠ ⎞λ2=0的特征向量α2=⎝ ⎛201⎠ ⎞,α3=⎝ ⎛010⎠ ⎞
2
3.分块法
6.3.3 新平方根公式
A = λ 1 G 1 + λ 2 G 2 + ⋯ + λ n G n 条件: A 正规,且 A = λ 1 G 1 + ⋯ + λ k G k \begin{aligned} &\sqrt{A}=\sqrt{\lambda_1}G_1+\sqrt{\lambda_2}G_2+\cdots+\sqrt{\lambda_n}G_n\\ &条件:A正规,且A=\lambda_1G_1+\cdots+\lambda_kG_k \end{aligned} A=λ1G1+λ2G2+⋯+λnGn条件:A正规,且A=λ1G1+⋯+λkGk
证明:
( A ) 2 = ( λ 1 G 1 + λ 2 G 2 + ⋯ + λ k G k ) 2 = λ 1 G 1 2 + λ 2 G 2 2 + ⋯ + λ k G k 2 = λ 1 G 1 + λ 2 G 2 + ⋯ + λ k G k \begin{aligned} (\sqrt{A})^2&=(\sqrt{\lambda_1}G_1+\sqrt{\lambda_2}G_2+\cdots+\sqrt{\lambda_k}G_k)^2\\ &=\lambda_1G_1^2+\lambda_2G_2^2+\cdots+\lambda_kG_k^2\\ &=\lambda_1G_1+\lambda_2G_2+\cdots+\lambda_kG_k \end{aligned} (A)2=(λ1G1+λ2G2+⋯+λkGk)2=λ1G12+λ2G22+⋯+λkGk2=λ1G1+λ2G2+⋯+λkGk
eg
A = ( 5 4 4 5 ) , 求 A A=\left( \begin{matrix} 5&4\\ 4&5 \end{matrix} \right),求\sqrt{A} A=(5445),求A
由于 A 为行和相等矩阵, ∴ λ ( A ) = { 9 , t r ( A ) − 9 } = { 9 , 1 } , 令 λ 1 = 9 , λ 2 = 1 ⇒ G 1 = A − λ 2 I λ 1 − λ 2 = 1 2 ( 1 1 1 1 ) , G 2 = A − λ 1 I λ 2 − λ 1 = 1 2 ( 1 − 1 − 1 1 ) ⇒ A = λ 1 G 1 + λ 2 G 2 = 3 G 1 + G 2 = ( 2 1 1 2 ) \begin{aligned} &由于A为行和相等矩阵,\therefore \lambda(A)=\{9,tr(A)-9\}=\{9,1\},令\lambda_1=9,\lambda_2=1\\ &\Rightarrow G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2}=\frac{1}{2}\left( \begin{matrix} 1&1\\1&1 \end{matrix} \right),G_2=\frac{A-\lambda_1I}{\lambda_2-\lambda_1}=\frac{1}{2}\left( \begin{matrix} 1&-1\\-1&1 \end{matrix} \right)\\ &\Rightarrow \sqrt{A}=\sqrt{\lambda_1}G_1+\sqrt{\lambda_2}G_2=3G_1+G_2=\left( \begin{matrix} 2&1\\1&2 \end{matrix} \right) \end{aligned} 由于A为行和相等矩阵,∴λ(A)={9,tr(A)−9}={9,1},令λ1=9,λ2=1⇒G1=λ1−λ2A−λ2I=21(1111),G2=λ2−λ1A−λ1I=21(1−1−11)⇒A=λ1G1+λ2G2=3G1+G2=(2112)