机器学习算法基础4-K-近邻算法、朴素贝叶斯算法、分类模型评估、模型的选择与调优3-sklearn数据集与估计器

一、K-近邻算法

1.定义

定义：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。
通俗来说，就是根据你的邻居来推断你的类别
来源：KNN算法最早是由Cover和Hart提出的一种分类算法

2.计算距离公式（欧氏距离）（重点）

相似的样本，特征之间的值应该都是相近的

两个样本的距离可以通过如下公式计算，又叫欧式距离
比如说，a(a1,a2,a3),b(b1,b2,b3)
√((a1-b1)^2+(a2-b2)^2+(a3-b3)^2 )
相似的样本，特征值应该是相近的

K-近邻算法需要对数据作标准化处理

3.sklearn k-近邻算法API

sklearn k-近邻算法API

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm='auto')
# 参数
n_neighbors：int,可选（默认= 5），k_neighbors查询默认使用的邻居数

algorithm：{‘auto’，‘ball_tree’，‘kd_tree’，‘brute’}，可选用于计算最近邻居的算法：
‘ball_tree’将会使用 BallTree，‘kd_tree’将使用 KDTree。
‘auto’将尝试根据传递给fit方法的值来决定最合适的算法。 (不同实现方式影响效率)

4.K-近邻算法实例-预测入住位置

实例流程：
1、数据集的处理
2、分割数据集
3、对数据集进行标准化
4、estimator流程进行分类预测


数据的处理-由于数据过大，做如下处理
1、缩小数据集范围
DataFrame.query()
2、处理日期数据
pd.to_datetime
pd.DatetimeIndex
3、增加分割的日期数据
4、删除没用的日期数据
pd.drop
5、将签到位置少于n个用户的删除
place_count =data.groupby('place_id').aggregate(np.count_nonzero)
tf = place_count[place_count.row_id > 3].reset_index()
data = data[data['place_id'].isin(tf.place_id)]

# K-近邻算法实例-预测入住位置

from sklearn.neighbors import KNeighborsClassifier
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import numpy as np

def knncls():
    '''K-近邻算法-预测用户入住位置
    return None
    '''
    # 一、数据集的处理
    # 读取数据
    data = pd.read_csv(r'C:\Users\admin\Desktop\v-predicting\train.csv')
    # 处理数据
    # 1.缩小数据-缩小数据集范围 DataFrame.query()查询数据筛选
    data = data.query('x>1.0 & x<1.25 & y>2.5 & y<2.75')

    # 2.处理时间数据
    time_value = pd.to_datetime(data['time'],unit='s')

    # 3、增加分割的日期数据
    # 把日期格式转化成字典格式
    time_value = pd.DatetimeIndex(time_value)
    # 根据时间  构造一些特征
    data.loc[:,'day'] = time_value.day
    data.loc[:,'hour'] = time_value.hour
    data.loc[:,'weekday'] = time_value.weekday


    # 4、删除没用的日期数据
    # 把时间戳特征删除,axis的重点在于方向而不在于行或列
        # axis = 0表示纵轴表示数据的变化从上至下，体现在行的增加与减少
        # axis = 1表示横轴表示数据的变化从左至右，体现在列的增加与减少
    data = data.drop(labels='time', axis=1)

    # 5.将签到位置少于n个用户的删除
    place_count = data.groupby('place_id').count()
    tf = place_count[place_count.row_id > 3].reset_index()
    # 过滤后的表格
    data = data[data['place_id'].isin(tf.place_id)]

    # 删除无用的row_id
    data = data.drop(labels='row_id', axis=1)
    print(data)

    # 取出数据中的目标值和特征值
    y = data["place_id"]
    x = data.drop(labels = 'place_id',axis=1)

    # 二、分割数据集
    # 进行数据的分割-训练集测试集
    x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=0.25)

    # 三、对数据集进行标准化
    # 特征工程（标准化）
    std = StandardScaler()

    # 对训练集与测试集的特征值进行标准化
    x_train = std.fit_transform(x_train)
    x_test = std.transform(x_test)



    # 四、estimator流程进行分类预测
    # 进行算法流程-estimator流程进行分类预测
    knn = KNeighborsClassifier(n_neighbors=5)
    knn.fit(x_train,y_train)
    # 得到预测结果
    y_predict = knn.predict(x_test)
    print('预测的目标签到位置为：', y_predict)

    # 得到预测的准确率-预测值与真实值进行比较
    print('预测的准确率为：',knn.score(x_test,y_test))

    return None


if __name__ == '__main__':
    knncls()
    
# 预测的目标签到位置为： [6424972551 1267801529 4932578245 ... 1228935308 4932578245 3992589015]
# 预测的准确率为： 0.474468085106383

5.通过k-近邻算法对生物物种进行分类——鸢尾花(load_iris)

# k近邻算法作业-•通过k-近邻算法对生物物种进行分类——鸢尾花(load_iris)
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

def knncls():
    '''通过K-近邻算法对生物物种进行分类'''
    # 一、数据集的处理
    li = load_iris()

    # 取数据集特征值与目标值
    x = li.data
    y = li.target

    # 二、分割数据集
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)

    # 三、对数据集进行标准化-特征工程
    std = StandardScaler()

    # 对训练集与测试集的特征值进行标准化
    x_train = std.fit_transform(x_train)
    x_test = std.transform(x_test)

    # 四、estimator流程进行分类预测
    # 超参数n_neighbors，可调
    knn = KNeighborsClassifier(n_neighbors=5)
    knn.fit(x_train,y_train)
    # 得到预测值
    y_predict = knn.predict(x_test)
    print('预测值是：\n',y_predict)

    # 预测准确率
    print('预测准确率是：\n',knn.score(x_test,y_test))
    return None

if __name__ == '__main__':
    knncls()
    
# 预测值是：
#  [2 2 0 1 1 2 2 2 0 0 1 1 0 2 1 0 0 0 0 0 1 1 1 1 1 2 1 2 2 2 2 2 2 0 0 0 2
#  2]
# 预测准确率是：
#  0.9210526315789473

6.k-近邻算法优缺点

问题：
1、k值取多大？有什么影响？
k值取很小：容易受异常点影响；k值取很大：容易受最近数据太多导致比例变化
2.性能问题

k-近邻算法优缺点
优点：简单，易于理解，易于实现，无需估计参数，无需训练

缺点：
懒惰算法，对测试样本分类时的计算量大，内存开销大
必须指定K值，K值选择不当则分类精度不能保证

使用场景：小数据场景，几千～几万样本，具体场景具体业务去测试

二、朴素贝叶斯算法

算出属于每个类别的概率，取最高的概率

1.概率基础

联合概率和条件概率：

联合概率：包含多个条件，且所有条件同时成立的概率，记作：P(A,B)

条件概率：就是事件A在另外一个事件B已经发生条件下的发生概率，记作：P(A|B)

特性：P(A1,A2|B) = P(A1|B)P(A2|B)
注意：此条件概率的成立，是由于A1,A2相互独立的结果
（自然语言处理不独立）

2.朴素贝叶斯原理介绍-特征相互独立(条件独立)

（朴素=>条件独立的意思）
朴素贝叶斯-贝叶斯公式

解决由于某个特征为0而造成概率为0的情况

拉普拉斯平滑-解决由于某个特征为0而造成概率为0的情况

解决方法：拉普拉斯平滑系数
P(F1│C)=(Ni+α)/(N+αm)            
α为指定的系数一般为1，m为训练文档中统计出的特征词个数

sklearn朴素贝叶斯实现API：sklearn.naive_bayes.MultinomialNB

MultinomialNB

sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
# 朴素贝叶斯分类
# 参数alpha：拉普拉斯平滑系数

3.朴素贝叶斯算法案例-sklearn20类新闻分类

朴素贝叶斯案例流程
20个新闻组数据集包含20个主题的18000个新闻组帖子

1、加载20类新闻数据，并进行分割
2、生成文章特征词
3、朴素贝叶斯estimator流程进行预估

# 朴素贝叶斯算法案例-sklearn20类新闻分类
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
def naviebayes():
    '''
    朴素贝叶斯进行文本分类
    :return:
    '''
    # 一、数据集处理
    #　1.加载数据集
    news = fetch_20newsgroups(subset='all')
    # 2.取得数据集的特征值与目标值
    x = news.data
    y = news.target
    # 3.分割数据集
    x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=0.25)

    # 二、对数据集进行特征抽取
    tf = TfidfVectorizer()

    # 以训练集当中的词的列表进行每篇文章重要性统计
    x_train = tf.fit_transform(x_train)
    # 打印单词列表
    print(tf.get_feature_names())

    x_test = tf.transform(x_test)

    # 三、朴素贝叶斯estimator流程进行预估
    mlt = MultinomialNB(alpha=1.0)
    print(x_train.toarray())
    mlt.fit(x_train,y_train)
    # 得到预测值
    y_predict = mlt.predict(x_test)
    print('预测值是：',y_predict)
    # 预测准确率
    print("预测准确率是：",mlt.score(x_test,y_test))

    return None

if __name__ == '__main__':
    naviebayes()

4.朴素贝叶斯算法的优缺点

不需要调参

朴素贝叶斯分类优缺点：

优点：
1.朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
2.对缺失数据不太敏感，算法也比较简单，常用于文本分类。
3.分类准确度高，速度快

缺点：
1.训练集误差大时，结果肯定不好；不允许调参
2.由于使用样本属性独立性的假设，故样本属性有关联时，其效果最好


神经网络的效果更好

三、分类模型评估

1.概念

分类模型的评估:
    
estimator.score()
# 一般最常见使用的是准确率，即预测结果正确的百分比

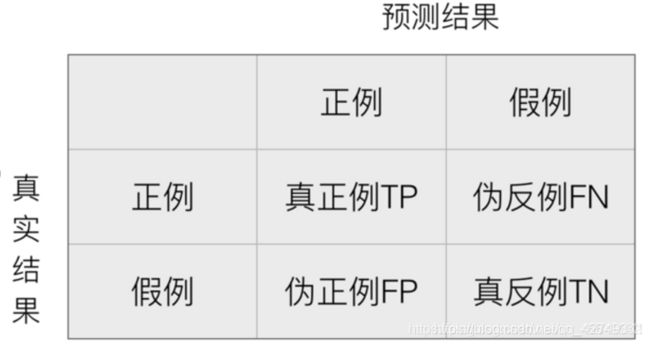
混淆矩阵
•在分类任务下，预测结果(Predicted Condition)
与正确标记(True Condition)之间存在四种不同的组合，构成混淆矩阵(适用于多分类)

召回率比较多

精确率：预测结果为正例样本中真实为正例的比例（查得准）
召回率：真实为正例的样本中预测结果为正例的比例（查的全，对正样本的区分能力）
其他分类标准，F1-score，反映了模型的稳健型

F1-score，反应了模型的稳健性

2.分类模型评估API

分类模型评估API:sklearn.metrics.classification_report

# 求每个类别的精确率和召回率
sklearn.metrics.classification_report(y_true, y_pred, target_names=None)
# 参数
y_true：真实目标值
y_pred：估计器预测目标值
target_names：目标类别名称
return：每个类别精确率与召回率

3.案例

# 精确率与召回率
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report

def naviebayes():
    '''
    朴素贝叶斯进行文本分类
    :return:
    '''
    # 一、数据集处理
    #　1.加载数据集
    news = fetch_20newsgroups(subset='all')
    # 2.取得数据集的特征值与目标值
    x = news.data
    y = news.target
    # 3.分割数据集
    x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=0.25)

    # 二、对数据集进行特征抽取
    tf = TfidfVectorizer()

    # 以训练集当中的词的列表进行每篇文章重要性统计
    x_train = tf.fit_transform(x_train)
    # 打印单词列表
    print(tf.get_feature_names())

    x_test = tf.transform(x_test)

    # 三、朴素贝叶斯estimator流程进行预估
    mlt = MultinomialNB(alpha=1.0)
    print(x_train.toarray())
    mlt.fit(x_train,y_train)
    # 得到预测值
    y_predict = mlt.predict(x_test)
    print('预测值是：',y_predict)
    # 预测准确率
    print("预测准确率是：",mlt.score(x_test,y_test))

    print('每个类别的精确率与召回率分别是:\n',classification_report(y_test,
    y_predict,target_names=news.target_names))

    return None

if __name__ == '__main__':
    naviebayes()
    
# 预测值是： [ 3  2 14 ...  9 15 14]
# 预测准确率是： 0.8433786078098472
# 每个类别的精确率与召回率分别是:
#                            precision    recall  f1-score   support
# 
#              alt.atheism       0.87      0.69      0.77       199
#            comp.graphics       0.89      0.75      0.81       250
#  comp.os.ms-windows.misc       0.78      0.87      0.82       221
# comp.sys.ibm.pc.hardware       0.72      0.82      0.77       234
#    comp.sys.mac.hardware       0.88      0.87      0.87       230
#           comp.windows.x       0.94      0.86      0.90       251
#             misc.forsale       0.92      0.66      0.77       255
#                rec.autos       0.90      0.92      0.91       242
#          rec.motorcycles       0.95      0.95      0.95       257
#       rec.sport.baseball       0.94      0.96      0.95       251
#         rec.sport.hockey       0.93      0.98      0.96       246
#                sci.crypt       0.85      0.97      0.90       261
#          sci.electronics       0.89      0.76      0.82       247
#                  sci.med       0.99      0.88      0.93       260
#                sci.space       0.88      0.98      0.93       258
#   soc.religion.christian       0.51      0.98      0.67       234
#       talk.politics.guns       0.70      0.97      0.81       216
#    talk.politics.mideast       0.93      0.98      0.95       232
#       talk.politics.misc       0.98      0.57      0.72       213
#       talk.religion.misc       1.00      0.17      0.29       155
# 
#                micro avg       0.84      0.84      0.84      4712
#                macro avg       0.87      0.83      0.82      4712
#             weighted avg       0.87      0.84      0.84      4712

四、模型的选择与调优

1.交差验证

交叉验证：为了让被评估的模型更加准确可信

交叉验证过程：
交叉验证：将拿到的数据，分为训练集和验证集。以下图为例：将数据分成5份，其中一份作为
验证集。然后经过5次(组)的测试，每次都更换不同的验证集。即得到5组模型的结果，取平
均值作为最终结果。又称5折交叉验证。

2.网格搜索-调超参数

超参数

超参数搜索-网格搜索
通常情况下，有很多参数是需要手动指定的（如k-近邻算法中的K值），这种叫超参数。
但是手动过程繁杂，所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证
来进行评估。最后选出最优参数组合建立模型。

多个超参数时，对模型预设多超参数组合，如，二个参数-两两组合、三个参数-三三组合，
每组超参数采用交叉验证(一般采用10折交叉验证)来进行评估，最后选出最优参数组合建立模型

1）超参数搜索-网格搜索API

超参数搜索-网格搜索API:sklearn.model_selection.GridSearchCV

sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)
# 对估计器的指定参数值进行详尽搜索

# 参数
estimator：估计器对象
param_grid：估计器参数(dict){“n_neighbors”:[1,3,5]}
cv：指定几折交叉验证

# 方法
fit：输入训练数据
score：准确率

#结果分析：
best_score_:在交叉验证中测试的最好结果
best_estimator_：最好的参数模型
cv_results_:每次交叉验证后的测试集准确率结果和训练集准确率结果

2）K-近邻算法调优 交叉验证与网格搜索

# K-近邻算法调优  交叉验证与网格搜索

from sklearn.neighbors import KNeighborsClassifier
import pandas as pd
from sklearn.model_selection import train_test_split,GridSearchCV
from sklearn.preprocessing import StandardScaler

def knncls():
    '''K-近邻算法-预测用户入住位置
    return None
    '''
    # 一、数据集的处理
    # 读取数据
    data = pd.read_csv(r'C:\Users\admin\Desktop\v-predicting\train.csv')
    # 处理数据
    # 1.缩小数据-缩小数据集范围 DataFrame.query()查询数据筛选
    data = data.query('x>1.0 & x<1.25 & y>2.5 & y<2.75')

    # 2.处理时间数据
    time_value = pd.to_datetime(data['time'],unit='s')

    # 3、增加分割的日期数据
    # 把日期格式转化成字典格式
    time_value = pd.DatetimeIndex(time_value)
    # 根据时间  构造一些特征
    data.loc[:,'day'] = time_value.day
    data.loc[:,'hour'] = time_value.hour
    data.loc[:,'weekday'] = time_value.weekday


    # 4、删除没用的日期数据
    # 把时间戳特征删除,axis的重点在于方向而不在于行或列
        # axis = 0表示纵轴表示数据的变化从上至下，体现在行的增加与减少
        # axis = 1表示横轴表示数据的变化从左至右，体现在列的增加与减少
    data = data.drop(labels='time', axis=1)

    # 5.将签到位置少于n个用户的删除
    place_count = data.groupby('place_id').count()
    tf = place_count[place_count.row_id > 3].reset_index()
    # 过滤后的表格
    data = data[data['place_id'].isin(tf.place_id)]

    # 删除无用的row_id
    data = data.drop(labels='row_id', axis=1)
    print(data)

    # 取出数据中的目标值和特征值
    y = data["place_id"]
    x = data.drop(labels = 'place_id',axis=1)

    # 二、分割数据集
    # 进行数据的分割-训练集测试集
    x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=0.25)

    # 三、对数据集进行标准化
    # 特征工程（标准化）
    std = StandardScaler()

    # 对训练集与测试集的特征值进行标准化
    x_train = std.fit_transform(x_train)
    x_test = std.transform(x_test)

    # 四、estimator流程进行分类预测
    # 进行算法流程-estimator流程进行分类预测
    knn = KNeighborsClassifier()

    # 五、算法调优-网格搜索
    # 构造一些参数的值进行搜索
    param = {'n_neighbors':[3,5,10]}
    gc = GridSearchCV(knn, param_grid=param, cv=2)

    gc.fit(x_train, y_train)

    # 预测准确率
    print('在测试集上的准确率：\n', gc.score(x_test, y_test))

    print('在交叉验证中最好的结果:\n',gc.best_score_)

    print('最好的参数模型：\n', gc.best_estimator_)

    print('每个超参数每次交叉验证后的结果：\n',gc.cv_results_)
    return None

if __name__ == '__main__':
    knncls()