二叉排序树与二叉搜索树
序言
二叉排序树
平衡二叉树
平衡二叉树
左旋转操作
平右旋转操作
双旋转操作
二叉排序树源码
平衡二叉搜索树源码
序言
- 当对数据进行查询或是删除,添加时
- 若使用数据进行存放数据,查询效率较高,但是增删效率低下(因为每次操作都要地洞若干数据)
- 若使用链表存放,则查询效率低下,因为每次都要遍历查询
- 一半情况下,若使用二叉排序树 ,则增删改查效率都比较高
- 但若数据构成的二叉排序树只有左子树或是只有右子树,则查询效率低下,优次引出了平衡二叉树
二叉排序树
-
二叉排序树
对于二叉排序树的任何一个非叶子节点,要求左节点的值比当前节点的值小,右节点的值比当前节点的值大(若有相同的值,放在左右节点都可) -
说明
二叉排序树的插入和删除效率较高 -
二叉排序树的删除
1、删除叶子节点
2、删除只有一颗子树的节点
3、删除有俩颗子树的节点
平衡二叉树
- 简介
当一颗二叉排序树的俩颗左右子树差距过大时,查询效率会非常低,由此,平衡二叉树又称为平衡二叉搜索数(AVL树),可以保证查询效率。它是一颗空树,或它的左右子树的高度之差的绝对值小于1。平衡二叉树的实现方法有:红黑树AVL(算法)、替罪羊树、Treap树、搜索树等等。
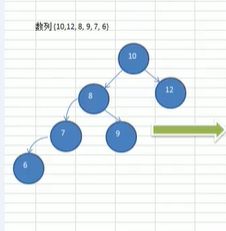
说明:当插入x是右子树的高度-左子树的高度大于1时,进行左旋转,判断是否需要双旋转,否则若进行右旋转时也需要是否需要双旋转
左旋转操作
- 创建一个新节点(newNode)(值等于当前根节点的值)
- 把新节点的左子树设置为当前节点的左子树 newNode.left =left;
- 把新节点的右子树设置为当前节点右子树的左子树 newNode.right = right.left;
- 把当前结点的值替换为右子节点的值 value = right.value;
- 把当前节点的右子树设置为右子树的右子树right = right.right;
- 把当前节点的左子树设置为新节点 left = newNode;
右旋转操作
-
创建一个新节点(newNode)(值等于当前根节点的值)
-
把新节点的右子树设置为当前节点的右子树 newNode.right
= right; -
把新节点的左子树设置为当前节点左子树的右子树 newNode.left = left.right;
-
把当前结点的值替换为左子节点的值 value = left.value;
-
把当前节点的左子树设置为左子树的左子树 left
= left.left; -
把当前节点的右子树设置为新节点 left = newNode;
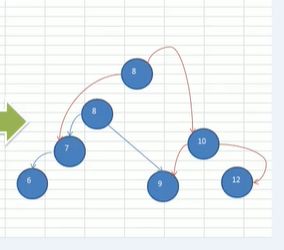
双旋转操作
符合右旋转操作时
- 当符合右旋转的操作
- 如果它的左子树的右子树的高度大于它的左子树的左子树高度
- 先对当前节点的左子节点进行左旋转
- 再对当前节点进行右节点操作即可
符合左旋转操作时
- 当符合左旋抓操作时
- 如果它的右子树的左子树高度大于它的右子树的右子树gaodu
- 先对当前节点右子树的左子节点进行右旋转
- 再对当前节点进行左旋转
二叉排序树源码
package com.guigu.binarysorttree;
public class BinarySortTreeDemo {
public static void main (String args[]) {
//测试
int[] arr = {7, 3, 10, 12, 5, 1, 9, 0};
BinarySortTree binarySortTree = new BinarySortTree();
//创建一颗二叉排序树
for (int i = 0; i < arr.length; i++) {
binarySortTree.add(new Node(arr[i]));
}
//中序遍历输出
System.out.println("中序输出二叉树");
binarySortTree.inFixOrder();
// //测试删除一个叶子节点
// binarySortTree.delNode(12);
// System.out.println("中序输出二叉树");
// binarySortTree.inFixOrder();
// //删除有一颗子树的节点
// binarySortTree.delNode(1);
// System.out.println("中序输出二叉树");
// binarySortTree.inFixOrder();
//删除有俩颗子树的节点
binarySortTree.delNode(7);
System.out.println("中序遍历二叉树");
binarySortTree.inFixOrder();
}
}
//创建二叉排序树
class BinarySortTree{
private Node root;
//查找待删除节点
public Node search(int value) {
//当前树为空树
if (root == null) {
return null;
} else {
return root.search(value);
}
}
//查找待删除节点的父节点
public Node searchParent(int value) {
//当前树为空树
if (root == null) {
return null;
} else {
return root.searchParent(value);
}
}
//删除节点
public void delNode(int value) {
//当前树为空树
if (root == null) {
return;
} else {
//找到待删除节点
Node targetNode = search(value);
//权值为value的节点不存在直接返回
if (targetNode == null) {
return;
}
//若该树只有一个根节点时,删除该根节点
if (root.left == null && root.right == null) {
root = null;
return;
}
//查找待删除节点的父节点
Node parent = searchParent(value);
//若待删除节点时叶子节点
if (targetNode.left == null && targetNode.right == null) {
//若targetNode是 parent的左节点
if (parent.left != null && parent.left == targetNode) {
parent.left = null;
} else if (parent.right != null && parent.right == targetNode) {
//若targetNode是 parent的右节点
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) { //若有俩颗子树
// //找到该待删除的节点的右子树的最小节点且删除
// int minValue = delRightTreeMin(targetNode.right);
// //将次最小值赋给他
// targetNode.value = minValue;
//从以待删除节点为根节点的左子树中找到最大值
int maxValue = delLeftTreeMax(targetNode.left);
//将最大值赋给它
targetNode.value = maxValue;
} else {//删除只有一颗子树的节点
//做targetNode 有左子树
if (targetNode.left != null) {
if (parent != null) {
//若targetNode为parent的左子节点
if (parent.left.value == value) {
parent.left = targetNode.left;
} else {
//targetNode 是 parent的右子节点
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else { //若targetNode 有右子树
if (parent != null) {
//若targetNode 为 parent的左子树
if (parent.left.value == value) {
parent.left = targetNode.right;
} else {
//做targetNode 为parent的右子树
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
//返回以node为根节点的二叉排序树的最小值,且删除该最小节点
public int delRightTreeMin(Node node) {
Node temp = node;
//沿着左子树找到最小节点
while (temp.left != null) {
temp = temp.left;
}
//删除该最小节点
delNode(temp.value);
//返回该最小值
return temp.value;
}
//返回以node为根节点的二叉排序树的最大值,且删除该节点
public int delLeftTreeMax(Node node) {
Node temp = node;
//沿着右子树查找
while (temp.right != null) {
temp = temp.right;
}
//删除该最大节点
delNode(temp.value);
//返回该最大值
return temp.value;
}
//添加节点创建二叉排序树
public void add(Node node) {
//当前树为空树直接指向根节点
if (root == null) {
root = node;
} else {
root.add(node);
}
}
//中序遍历
public void inFixOrder() {
//当前树不为空树是遍历
if (root != null) {
root.inFixOrder();
} else {
System.out.println("当前树为空树");
}
}
}
//创建节点
class Node{
int value;
Node left;
Node right;
//节点构造器
public Node(int value) {
this.value = value;
}
//查找节点(按照节点权值查找)
public Node search (int value) {
//当前节点权值等于它直接返回
if (this.value == value) {
return this;
} else if (value < this.value) {
//当前节点权值大于待查找节点
//当当前节点左子节点为空时
if (this.left == null) {
return null;
}
return this.left.search(value);
} else {
//若当前节点值小于待查找节点
//当前节点右子节点为空
if (this.right == null) {
return null;
}
return this.right.search(value);
}
}
//查找当前节点的父节点
public Node searchParent(int value) {
//若当前节点即为待查找节点的父节点
if ((this.left != null && this.left.value == value) ||
(this.right != null && this.right.value == value)) {
return this;
} else {
//当前节点不是,则分别向左子树和右子树查找
//当待查找结点的值小于当前节点且当前节点左子树非空时
if (value < this.value && this.left != null) {
//左子树递归查找
return this.left.searchParent(value);
} else if (value >= this.value && this.right != null) {
//右子树递归查找
return this.right.searchParent(value);
} else {
return null; //没有找到
}
}
}
//通过递归添加节点
public void add(Node node) {
//递归终止条件
if (node == null) {
return;
}
//判断传入的节点的权值和当前节点的大小
if (node.value < this.value) {
//判断当前节点左子树是否为空
if (this.left == null) {
this.left = node;
} else {
//否则递归添加
this.left.add(node);
}
} else {
//判断当前节点右子树是否为空
if (this.right == null) {
this.right = node;
} else {
//否则递归添加
this.right.add(node);
}
}
}
//中序遍历排序树
public void inFixOrder() {
//当前节点左子树非空
if (this.left != null) {
this.left.inFixOrder();
}
//输出当前节点
System.out.println(this);
//输出当前节点又节点
if (this.right != null) {
this.right.inFixOrder();
}
}
/**
* 删除叶子节点
* 1、首先找到待删除的节点targetNode
* 2、找到targetNode节点的父节点 parent
* 3、确定 targetNode是 parent的左子节点还是右子节点
* 4、 左子节点 parent.left = null;
* 右子节点 parent.right = null;
* */
/**
* 删除只有一颗子树的节点
* 1、手先找到待删除节点 targetNode
* 2、找到targetNode节点的父节点parent
* 3、且确定targetNode的节点是左子节点还是右子节点
* 4、targetNode是parent的左子节点还是右子节点
* 5、若targetNode有左子节点
* 5.1 targetNode是parent的左节点
* parent.left = targetNode.left;
* 5.2targetNode是parent的右子节点
* parent.right = targetNode.left;
* 6、若targetNode有右子节点
* 6.1 targetNode 是parent的左节点
* parent.left = target.right;
* 6.2 targetNode 是 parent的右节点
* parent.right = target.right;
*
*
* */
/** 节点含有俩颗子树
* 1、找到待删除节点 targetNode
* 2、找到待删除节点的父节点 parent
* 3、从targetNode的右子树找到权值最小的节点(或从左子树找到最大的权值)
* 4、定义一个临时变量将权值最小的保存temp = 11
* 5、删除该最小节点(或删除该最大节点)
* 6、targetNode.value = temp
*
* */
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
}
平衡二叉树源码
package com.guigu.avl;
public class AVLTreeDemo {
public static void main (String args[]) {
//int[] arr = {4, 3, 6, 5, 7, 8};
//int[] arr = {10, 12, 8, 9, 7, 6};
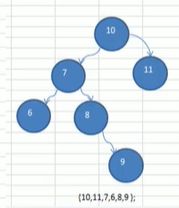
int[] arr = {10, 11, 7, 6, 8, 9};
//创建一颗AVL树
AVLTree avlTree = new AVLTree();
for (int i = 0; i < arr.length; i++) {
avlTree.add(new Node(arr[i]));
}
System.out.println("没做处理之前的");
System.out.println("中序遍历二叉树");
avlTree.inFixOrder();
System.out.println("二叉排序是的高度为:" + avlTree.getRoot().height());
System.out.println("二叉排序树的左子树的高度为:" + avlTree.getRoot().leftHeight());
System.out.println("二叉排序树的右子树的高度为:" + avlTree.getRoot().rightHeight());
}
}
//创建AVL树
class AVLTree{
private Node root;
public Node getRoot() {
return root;
}
//查找待删除节点
public Node search(int value) {
//当前树为空树
if (root == null) {
return null;
} else {
return root.search(value);
}
}
//查找待删除节点的父节点
public Node searchParent(int value) {
//当前树为空树
if (root == null) {
return null;
} else {
return root.searchParent(value);
}
}
//删除节点
public void delNode(int value) {
//当前树为空树
if (root == null) {
return;
} else {
//找到待删除节点
Node targetNode = search(value);
//权值为value的节点不存在直接返回
if (targetNode == null) {
return;
}
//若该树只有一个根节点时,删除该根节点
if (root.left == null && root.right == null) {
root = null;
return;
}
//查找待删除节点的父节点
Node parent = searchParent(value);
//若待删除节点时叶子节点
if (targetNode.left == null && targetNode.right == null) {
//若targetNode是 parent的左节点
if (parent.left != null && parent.left == targetNode) {
parent.left = null;
} else if (parent.right != null && parent.right == targetNode) {
//若targetNode是 parent的右节点
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) { //若有俩颗子树
// //找到该待删除的节点的右子树的最小节点且删除
// int minValue = delRightTreeMin(targetNode.right);
// //将次最小值赋给他
// targetNode.value = minValue;
//从以待删除节点为根节点的左子树中找到最大值
int maxValue = delLeftTreeMax(targetNode.left);
//将最大值赋给它
targetNode.value = maxValue;
} else {//删除只有一颗子树的节点
//做targetNode 有左子树
if (targetNode.left != null) {
if (parent != null) {
//若targetNode为parent的左子节点
if (parent.left.value == value) {
parent.left = targetNode.left;
} else {
//targetNode 是 parent的右子节点
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else { //若targetNode 有右子树
if (parent != null) {
//若targetNode 为 parent的左子树
if (parent.left.value == value) {
parent.left = targetNode.right;
} else {
//做targetNode 为parent的右子树
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
//返回以node为根节点的二叉排序树的最小值,且删除该最小节点
public int delRightTreeMin(Node node) {
Node temp = node;
//沿着左子树找到最小节点
while (temp.left != null) {
temp = temp.left;
}
//删除该最小节点
delNode(temp.value);
//返回该最小值
return temp.value;
}
//返回以node为根节点的二叉排序树的最大值,且删除该节点
public int delLeftTreeMax(Node node) {
Node temp = node;
//沿着右子树查找
while (temp.right != null) {
temp = temp.right;
}
//删除该最大节点
delNode(temp.value);
//返回该最大值
return temp.value;
}
//添加节点创建二叉排序树
public void add(Node node) {
//当前树为空树直接指向根节点
if (root == null) {
root = node;
} else {
root.add(node);
}
}
//中序遍历
public void inFixOrder() {
//当前树不为空树是遍历
if (root != null) {
root.inFixOrder();
} else {
System.out.println("当前树为空树");
}
}
}
//创建节点
class Node{
int value;
Node left;
Node right;
//返回左子树的高度
public int leftHeight() {
if (left == null) {
return 0;
}
return left.height();
}
//返回右子树额高度
public int rightHeight() {
if (right == null) {
return 0;
}
return right.height();
}
//返回以该节点为根节点的树的高度
public int height() {
return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
}
//左旋转方法
private void leftRotate() {
//创建一个新节点,权值为当前根节点的权值
Node newNode = new Node(value);
//新节点的左子树为当前节点的左子树
newNode.left = left;
//新节点的右子树为当前节点的右子树的右子树
newNode.right = right.right;
//把当前节点的权值改为当前节点右子节点的权值
value = right.value;
//当前节点的右子树为它的右子树的右子树
right = right.right;
//当前节点的左子树为新节点
left = newNode;
}
//右旋转方法
private void rightRotate() {
//创建一个新节点权值等于当前根节点的权值
Node newNode = new Node(value);
//新节点的右子树为当前节点的右子树
newNode.right = right;
//新节点的左子树为当前节点左子树的右子树
newNode.left = left.right;
//把当前节点的权值改为当前节点左节点的权值
value = left.value;
//当前节点左子树为它的左子树的左子树
left = left.left;
//当前节点的右子树为新节点
right = newNode;
}
//节点构造器
public Node(int value) {
this.value = value;
}
//查找节点(按照节点权值查找)
public Node search (int value) {
//当前节点权值等于它直接返回
if (this.value == value) {
return this;
} else if (value < this.value) {
//当前节点权值大于待查找节点
//当当前节点左子节点为空时
if (this.left == null) {
return null;
}
return this.left.search(value);
} else {
//若当前节点值小于待查找节点
//当前节点右子节点为空
if (this.right == null) {
return null;
}
return this.right.search(value);
}
}
//查找当前节点的父节点
public Node searchParent(int value) {
//若当前节点即为待查找节点的父节点
if ((this.left != null && this.left.value == value) ||
(this.right != null && this.right.value == value)) {
return this;
} else {
//当前节点不是,则分别向左子树和右子树查找
//当待查找结点的值小于当前节点且当前节点左子树非空时
if (value < this.value && this.left != null) {
//左子树递归查找
return this.left.searchParent(value);
} else if (value >= this.value && this.right != null) {
//右子树递归查找
return this.right.searchParent(value);
} else {
return null; //没有找到
}
}
}
//通过递归添加节点
public void add(Node node) {
//递归终止条件
if (node == null) {
return;
}
//判断传入的节点的权值和当前节点的大小
if (node.value < this.value) {
//判断当前节点左子树是否为空
if (this.left == null) {
this.left = node;
} else {
//否则递归添加
this.left.add(node);
}
} else {
//判断当前节点右子树是否为空
if (this.right == null) {
this.right = node;
} else {
//否则递归添加
this.right.add(node);
}
}
/**
* 此处调整为一颗平衡二叉排序树
* */
//当添加完一个节点后:右子树的高度 - 左子树的高度 > 1则左旋转
if (rightHeight() - leftHeight() > 1) {
//如果当前节点的右子树的左子树高度大于右子树的右子树的高度
if (right != null && right.leftHeight() > right.rightHeight()) {
//对当前节点的右子节点进行右旋转
right.rightRotate();
//当前节点左旋转
leftRotate();
} else {
leftRotate();
}
//这里注意要处理之后直接返回,否则会处理多次
return;
}
//当添加完一个节点后,左子树的高度 - 右子树的高度 > 1 则右旋转
if (leftHeight() - rightHeight() > 1) {
//判断是否需要双旋转
//如果当前节点的左子树的右子树的高度大于当前节点左子树的左子树的高度
if (left != null && left.rightHeight() > left.leftHeight()) {
//对当前节点的左子节点进行左旋转
left.leftRotate();
//对当前节点进行右旋转
rightRotate();
} else {
rightRotate();
}
}
}
//中序遍历排序树
public void inFixOrder() {
//当前节点左子树非空
if (this.left != null) {
this.left.inFixOrder();
}
//输出当前节点
System.out.println(this);
//输出当前节点又节点
if (this.right != null) {
this.right.inFixOrder();
}
}
/**
* 删除叶子节点
* 1、首先找到待删除的节点targetNode
* 2、找到targetNode节点的父节点 parent
* 3、确定 targetNode是 parent的左子节点还是右子节点
* 4、 左子节点 parent.left = null;
* 右子节点 parent.right = null;
* */
/**
* 删除只有一颗子树的节点
* 1、手先找到待删除节点 targetNode
* 2、找到targetNode节点的父节点parent
* 3、且确定targetNode的节点是左子节点还是右子节点
* 4、targetNode是parent的左子节点还是右子节点
* 5、若targetNode有左子节点
* 5.1 targetNode是parent的左节点
* parent.left = targetNode.left;
* 5.2targetNode是parent的右子节点
* parent.right = targetNode.left;
* 6、若targetNode有右子节点
* 6.1 targetNode 是parent的左节点
* parent.left = target.right;
* 6.2 targetNode 是 parent的右节点
* parent.right = target.right;
*
*
* */
/** 节点含有俩颗子树
* 1、找到待删除节点 targetNode
* 2、找到待删除节点的父节点 parent
* 3、从targetNode的右子树找到权值最小的节点(或从左子树找到最大的权值)
* 4、定义一个临时变量将权值最小的保存temp = 11
* 5、删除该最小节点(或删除该最大节点)
* 6、targetNode.value = temp
*
* */
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
}