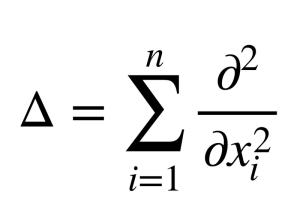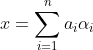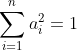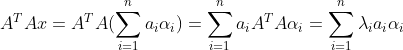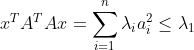ORB点特征、LSD线特征、线特征参数化求导学习总结

目录

1 ORB特征点

LSD特征线

什么是图像的线特征

什么是梯度算子（也叫一阶差分算子）

 如何利用算子进行边缘提取（通过卷积，什么是卷积？）

三种一阶差分算子

1. Roberts算子

2.Sobel算子

 3.Prewitt算子

 二阶差分算子

 1.拉普拉斯算子(Laplace)

3.Canny算子

计算机视觉中Canny算子详解_计算机秃头选手的博客-CSDN博客_canny算子

LSD线特征提取参考博客

SLAM中线特征的参数化和求导

矩阵奇异值与矩阵范数之间有什么联系？

---

我们要知道三维空间中的点在图像中的位置，就需要提取特征与特征匹配了。

1 ORB特征点

提取步骤：1.检测特征点  2.计算描述子  3.特征匹配

1.检测特征点

　　ORB用到的检测特征点的方法是Oriented FAST算法，最大的特点就是快！

　　算法原理：

①遍历图像，找到所有的角点。

②例如只拿到一个角点p，设其像素灰度值为I，取这个角点以三为半径的圆上的所有像素点，能取到16个，

③然后设定一个阈值t，如果连续n个像素点的灰度值都大于I+t或者都小于I-t。我们则认为其为特征点。

④接着计算方向：特征点与重心的角度。

2.计算描述子

   　描述子我们可以理解为在每一个特征点旁边有一个向量，或者说也可以理解为数组，记录着特征点周围的信息。这里用的事BRIEF描述子。BRIEF描述子是一个二进制描述子，就是在特征点周围随机取128对点对或者是256对点对p和q，若p大于q，则记为1，否则记为0。这就组成了一个128个数的[0,1,1,0.....]序列。

3.特征匹配

　　此时我们得到了所有的特征点和描述子。此时进行暴力匹配，对图1中的每一个特征点分别和图像2中的特征点的描述子比较，我们用Hamming距离来度量两个描述子的相似程度，如果Hamming距离小于两倍的最小距离则认为匹配正确，否则认为匹配错误。

#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;

int main ( int argc, char** argv )
{
    if ( argc != 3 )
    {
        cout<<"usage: feature_extraction img1 img2"< keypoints_1, keypoints_2;
    Mat descriptors_1, descriptors_2;
    Ptr detector = ORB::create();
    Ptr descriptor = ORB::create();
    Ptr matcher  = DescriptorMatcher::create ( "BruteForce-Hamming" );

    //-- 第一步:检测 Oriented FAST 角点位置
    detector->detect ( img_1,keypoints_1 );
    detector->detect ( img_2,keypoints_2 );

    //-- 第二步:根据角点位置计算 BRIEF 描述子
    descriptor->compute ( img_1, keypoints_1, descriptors_1 );
    descriptor->compute ( img_2, keypoints_2, descriptors_2 );

    Mat outimg1;
    drawKeypoints( img_1, keypoints_1, outimg1, Scalar::all(-1), DrawMatchesFlags::DEFAULT );
    imshow("ORB特征点",outimg1);

    //-- 第三步:对两幅图像中的BRIEF描述子进行匹配，使用 Hamming 距离
    vector matches;//matches存储特征点信息
    matcher->match ( descriptors_1, descriptors_2, matches );

    //-- 第四步:匹配点对筛选
    double min_dist=10000, max_dist=0;

    //找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
    for ( int i = 0; i < descriptors_1.rows; i++ )
    {
        double dist = matches[i].distance;
        if ( dist < min_dist ) min_dist = dist;
        if ( dist > max_dist ) max_dist = dist;
    }

    printf ( "-- Max dist : %f \n", max_dist );
    printf ( "-- Min dist : %f \n", min_dist );

    //当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
    std::vector< DMatch > good_matches;
    for ( int i = 0; i < descriptors_1.rows; i++ )
    {
        if ( matches[i].distance <= max ( 2*min_dist, 30.0 ) )
        {
            good_matches.push_back ( matches[i] );
        }
    }

    //-- 第五步:绘制匹配结果
    Mat img_match;
    Mat img_goodmatch;
    drawMatches ( img_1, keypoints_1, img_2, keypoints_2, matches, img_match );
    drawMatches ( img_1, keypoints_1, img_2, keypoints_2, good_matches, img_goodmatch );
    imshow ( "所有匹配点对", img_match );
    imshow ( "优化后匹配点对", img_goodmatch );
    waitKey(0);

    return 0;
}

LSD特征线

什么是图像的线特征

①影像的边缘或线认为是图像的线特征；
②“边缘”可定义为影像局部区域特征不相同的那些区域间的 分界线，
③而“线”则可以认为是具有很小宽度的其中间区域 具有相同的影像特征的边缘对

线特征提取的应用
1.房屋提取
2.道路提取

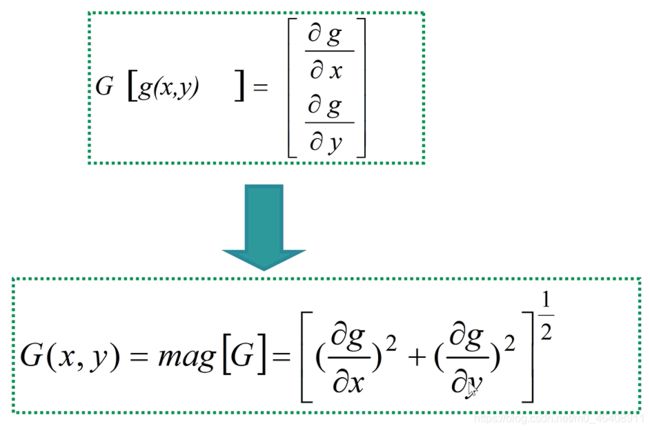
什么是梯度算子（也叫一阶差分算子）

g(x,y)为图像某点处的灰度值；梯度算子即为对x，y方向求偏导数（如何对数字影像求导数请参见该文章前些部分的介绍影像的导数

 如何利用算子进行边缘提取（通过卷积，什么是卷积？）

以sobel算子为例学习一下如何进行卷积

三种一阶差分算子

1. Roberts算子

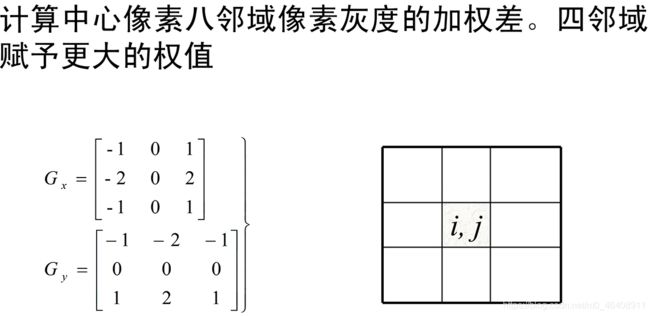
2.Sobel算子

计算中心像素八领域像素灰度的加权差，四领域赋予更大的权值。

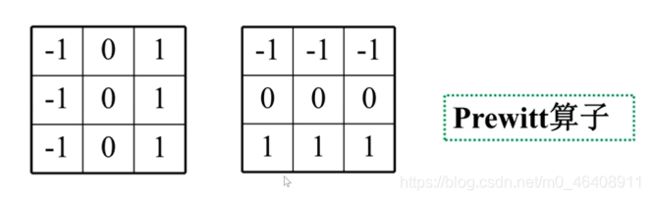
 3.Prewitt算子

与Sobel算子模板类似

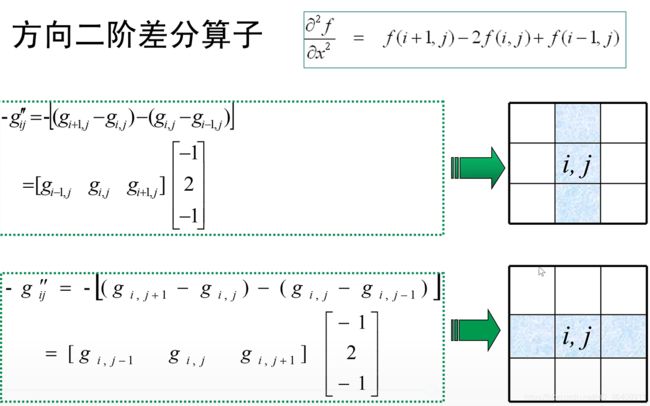
 二阶差分算子

 1.拉普拉斯算子(Laplace)

在数学以及物理中，拉普拉斯算子或是拉普拉斯算符（英语：Laplace operator, Laplacian）是由欧几里得空间中的一个函数的梯度的散度给出的微分算子，通常写成 、 

​

编辑

 2.高斯-拉普拉斯算子（LOG)

LoG算子也就是 Laplace of Gaussian function(高斯拉普拉斯函数)。常用于数字图像的边缘提取和二值化。LOG 算子源于D.Marr计算视觉理论中提出的边缘提取思想, 即首先对原始图像进行最佳平滑处理, 最大程度地抑制噪声, 再对平滑后的图像求取边缘。

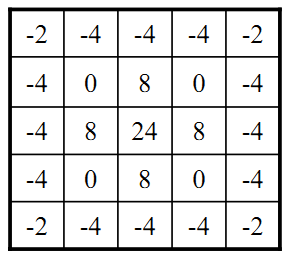
常用的LoG算子是5×5的模板，高斯拉普拉斯函数：

3.Canny算子

通常情况下边缘检测的目的是在保留原有图像属性的情况下，显著减少图像的数据规模。有多种算法可以进行边缘检测，虽然Canny算法年代久远，但可以说它是边缘检测的一种标准算法，而且仍在研究中广泛使用。

Canny的实现步骤

①应用高斯滤波来平滑图像，目的是去除噪声
②找寻图像的强度梯度（intensity gradients）
③应用非最大抑制（non-maximum suppression）技术来消除边误检（本来不是但检测出来是）
④应用双阈值的方法来决定可能的（潜在的）边界
⑤利用滞后技术来跟踪边界

计算机视觉中Canny算子详解_计算机秃头选手的博客-CSDN博客_canny算子

LSD线特征提取参考博客

论文笔记-LSD: a Line Segment Detector线特征提取_wrotcat的博客-CSDN博客_lsd线特征提取

---

SLAM中线特征的参数化和求导

众所周知，线特征比点特征可以提供更多的约束条件，并且在某些场合下比点特征要鲁棒。但是如果我们想要把线特征加入到SLAM系统中面临的是参数化和优化求导。

下面我们就来详细介绍一下空间直线的两种参数化方法：①Plücker参数化方法，②直线正交表示方法。为什么需要两种参数化方法呢？因为空间中的直线有4个自由度，而Plücker参数化方法需要使用6个参数表示直线，这样就会导致过参数化，过参数化在优化的时候就需要采用带约束的优化，不太方便。于是引入了可以用4个参数更新直线的正交表示来方便优化。这两种参数化方法可以很方便的相互转换，所以我们可以在SLAM系统中同时使用这两种参数化形式，在初始化和进行空间变换的时候使用Plücker坐标，在优化的时候使用正交表示。下面我们就来详细了解这两种参数化方法和优化的雅克比求导。

1、Plücker参数化方法

普吕克坐标法线特征参数化详见SLAM中线特征的参数化和求导 - 知乎
 

矩阵奇异值与矩阵范数之间有什么联系？

首先可以定义欧式空间的向量x的范数，同时基于每一种向量范数，可以相应地定义矩阵A的范数为

向量的范数存在多种定义方式，最常见的是2范数，也就是欧式空间的长度：

那么相应的矩阵A的范数即为当时，函数的最大值。

注意是对称非负定矩阵，特征值满足，相应的特征向量构成的一组标准正交基，那么设

根据知道有

于是

可知，即的最大特征值的平方根，即A的最大奇异值。

---

参考文献

数字摄影测量之线特征提取算子——有差分算子、拉普拉斯算子、LOG算子_琳噶酱ざ的博客-CSDN博客_特征提取拉普拉斯算子
ORB-SLAM2代码实现之灰度质心法学习记录_weixin_46427781的博客-CSDN博客_灰度质心法
计算机视觉中Canny算子详解_计算机秃头选手的博客-CSDN博客_canny算子

 

SLAM中线特征的参数化和求导 - 知乎

点线结合 PL-VINS ：线特征提取(feature-tracker) 代码整理笔记_长夜临光的博客-CSDN博客_线特征提取