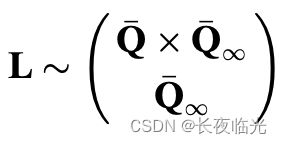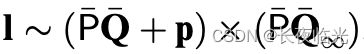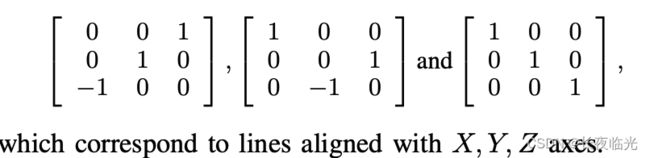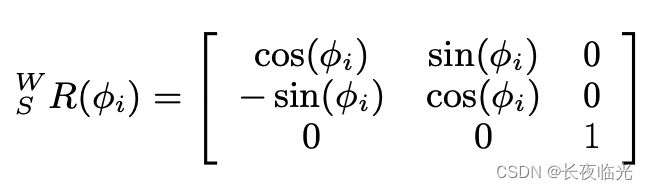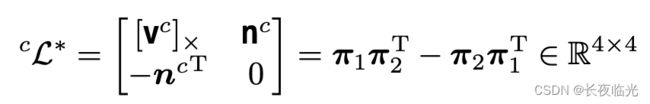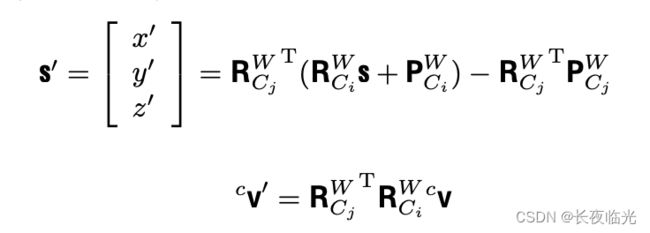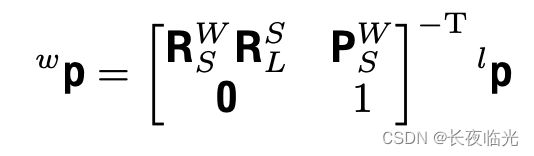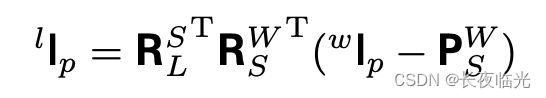SLAM中线特征的参数化表示方法/重投影/初始化方法

由于最近在做结构信息辅助的SLAM，在线特征这块很多概念诸如参数化表示方法(包括普通线和结构线) 、初始化和优化方法等，相比点特征的处理更为复杂，因此这篇文章算是线特征学习的一个阶段性总结。

深度参考了以下资料：

1. 什么是齐次坐标?
2. Structure-From-Motion Using Lines: Representation, Triangulation and Bundle Adjustment
3. SLAM线特征学习（1）——基本的线特征表示与优化推导
4. SLAM线特征学习（2）——线特征初始化和最小表示

1. 预备知识

由于涉及到计算机多视图几何中的一些知识，为方便理解在此把一些重要概念列出。

齐次坐标

欧式空间下的笛卡尔坐标可以很好的用来描述二维/三维的空间几何并解决相关数学运算问题，但在计算机视觉领域下的投影空间中存在着许多无法解释和处理的问题，如：两条平行线在投影空间中的相交问题（这也是结构线SLAM中对Vanish Point 灭点/消影点的提取和利用的前提）

图1. 现实世界中相互平行的铁轨，竟然在投影空间中可以相交于无限远处的地平线

在欧氏空间中，我们无法描述这样一个存在于无穷远的点，无穷的坐标并不是我们想要在参数化和优化过程中想要看到的。因此，由 August Ferdinand Möbius提出的齐次坐标，就是用来解决这样一类问题的，它使图形和几何学的计算在投影空间中成为可能。

齐次坐标的本质，就是用 N + 1 个数来表示 N 维坐标，所额外增加的这个参数在表示不同几何体的情况下会具备不同的几何意义。

对于欧氏空间中坐标表示为 $(X,Y,Z)$ 的空间点(显然有3个自由度），额外引入一个变量 $w$，我们就可以构建该空间点的齐次坐标 $(x,y,z,w)$，其中$X=x/w,Y=y/w,Z=z/w$，在这里 $w$ 的几何意义就是 逆深度 ，也是SLAM中点特征参数化的常见概念。这里之所以叫“齐次坐标”，就是因为对齐次坐标乘上任意一个非零系数，在欧氏空间中都对应着同一个点。

在本文后续将以 ${\mathbf{M}}^T=(\overline{\mathbf{M}},m{)}^T$ 的齐次坐标形式来表示一个空间点。

～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～
对投影空间中两平行线相交于一点的证明
在二维欧氏空间下的两条空间线方程联立即可得到交点，如下：

$$\{\begin{array}{l}Ax+By+C=0\\ Ax+By+D=0\end{array}$$
显然当 $C\ne D$的情况下 ，欧氏空间下方程组无解。若用齐次坐标重写投影空间下的方程组如下：

很明显现在 $Cw$ 可以等于 $Dw$ 了，也就是当 $w=0$ （逆深度为0也就是无穷远）的时候有解 $(x,y,0)$，这个解在投影几何上也称作为Vanish Point（灭点/消失点/消影点）。
～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～

齐次坐标在计算机图形学中是非常有用的基本概念，通过增加一个额外的维度W后，可以用来对几何体进行缩放,旋转,平移,透视投影的矩阵变换.

现在从空间点过渡到空间平面。由于3D射影空间下点和面的对偶性，我们同样用类似的齐次坐标形式来表示射影空间中的一个平面 $(x,y,z,w)$（仍然是3个自由度：平面上的二维位移+绕法向量的旋转），其中 $\text{n}=(x,y,z{)}^T$ 对应欧氏空间中的该平面法向量，对平面上任一点 $\text{P}=(X,Y,Z{)}^T$ 有 ${\text{n}}^T\text{P}+w=0$（也就是空间平面方程 Ax+By+Cz+D=0），其中 $w/||\text{n}||$ 为原点到平面的距离。

在本文后续也会以 ${\mathbf{P}}^T=(\overline{\mathbf{P}},p{)}^T$ 的齐次坐标形式来表示一个空间平面。

---

空间直线的优化

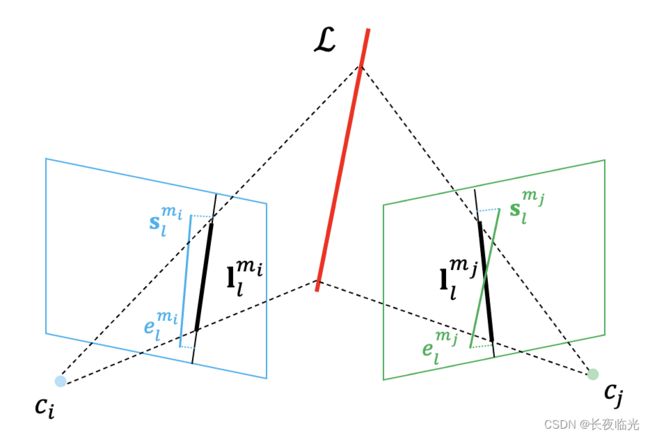
在SLAM问题的BA优化问题中，给定第 $l$ 条空间直线在第 $i$ 帧相机归一化平面下的观测为线段起点 ${\mathbf{s}}_l^{m_i}=(u_s,v_s,1{)}^T$ 和线段终点 ${\mathbf{e}}_l^{m_i}=(u_e,v_e,1{)}^T$ ，根据当前直线参数得到的直线与相机原点构成平面的法向量为 ${\mathbf{n}}_c$，则重投影直线方程即为 ${\mathbf{l}}_l^{m_i}=({\mathbf{n}}_c(0),{\mathbf{n}}_c(1),{\mathbf{n}}_c(2){)}^T$ 。
空间线的重投影误差定义为：
$${\mathbf{r}}_{L_l}^{c_i}=\frac{1}{||{\mathbf{z}}_{L_l}^{m_i}||}\left(\begin{array}{c}d({\mathbf{s}}_l^{m_i},{\mathbf{l}}_l^{m_i})\\ d({\mathbf{e}}_l^{m_i},{\mathbf{l}}_l^{m_i})\end{array}\right)$$其中 $d(\mathbf{s},\mathbf{l})$ 为端点 $s$ 到投影直线 $l$ 的距离，如下：
$$d(\mathbf{s},\mathbf{l})=\frac{{\mathbf{s}}^T\mathbf{l}}{\sqrt{l_1^2+l_2^2}}$$
误差量示意图如下：

---

2. 空间直线的表示方法

我们将描述多种投影空间中表示3D直线的方法及其特性。其中一些表示法在某些场景下是“片面的”，只能表示所有3D线的一个子集。例如，在尺度重建中要求重建的直线不能位于无穷远处。

研究空间直线的表示方法的意义在于选择一种合适的表示法来解决三角化和BA优化的问题。

• 对于三角化，最重要的准则是：重投影的直线是3D空间直线的线性函数。
• 对于BA优化，由于本质上是一个非线性过程，为直线的参数化提供了更灵活的选择空间。
• 参数化的质量评估，应取决于自由度和约束的数量。

2.1 空间直线的自由度

一条直线的空间自由度为 4，它既可以看作是两个空间点的连接(join)，也可以看作是两个空间平面的相交(intersection)，可以从不同角度去理解这个空间自由度为4:

1. 直线自身角度：绕直线自身旋转和沿直线方向移动，直线不变，因此自由度为 6 - 2 = 4。
2. 平面相交角度：两个空间平面的自由度为 3 x 2 = 6，两个平面以直线为轴旋转，直线不变，因此自由度为 (3-1) x 2 = 4。
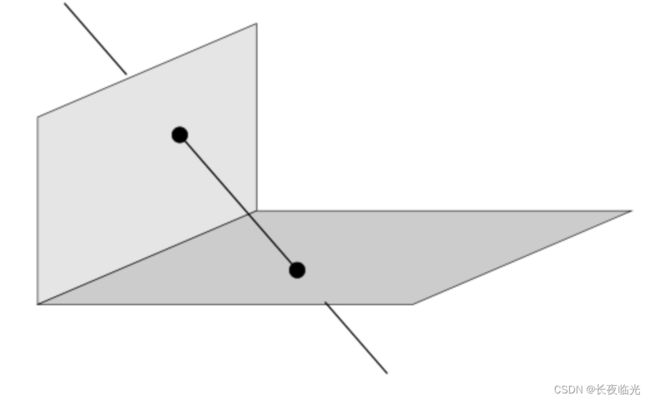
3. 两点连接角度：将直线看作是穿过两个正交平面的交点所连接起来的几何体，则两个交点在各自平面上只有2个自由度，因此直线自由度为 2 x 2 = 4，如图

2.2 普吕克坐标 (Plucker Coordinates Representation)

普吕克坐标是一种比较简单的对一条直线进行唯一确定的坐标表示方法，也是一种可以表示所有直线的完备表示方法，许多其他直线的表示方法也可以和普吕克坐标进行互换。
普吕克坐标最直观的理解就是用直线上两点的向量差（线的方向向量）和两点的向量叉乘（极平面的法向量） 这六个参数来表示一条直线，设普吕克坐标为 ${\mathbf{L}}^T=({\mathbf{a}}^T,{\mathbf{b}}^T{)}^T$，其中 $\mathbf{a}$ 和 $\mathbf{b}$ 可分别对应下图中的法向量 $\mathbf{m}$ 或 方向向量 $\mathbf{d}$，在不同论文中的表述不是非常统一，本文中令 $\mathbf{a}$ 为法向量并用 $\mathbf{n}$（normal）表示，$\mathbf{b}$ 为直线方向向量并用 $\mathbf{v}$（vector）来表示，即 ${\mathbf{L}}^T=({\mathbf{n}}^T,{\mathbf{v}}^T{)}^T$。

直线的唯一确定原理

对一条空间直线的唯一确定表示来说，比较直观的三个要素是直线的方向 $\mathbf{v}$ ，直线和极点构成平面的法向量 $\mathbf{n}$ 和直线到原点的距离 $d$，其中：

1. 用方向向量 $\mathbf{v}$ 和 距离 $d$ 来表示，如下图1，只能确定一个圆（为了方便直观理解，取一条沿着 $Z$ 轴方向的直线并用黄色标注）
2. 用法向量 $\mathbf{n}$ 和距离 $d$ 来表示，如下图2，同样只能确定一个圆（注意与 $\mathbf{v}$ & $d$ 确定的圆区分）
3. 用法向量 $\mathbf{v}$ & $\mathbf{n}$ & $d$ 一起来表示，如下图3，可以唯一确定一条直线（虽然存在两个交点，但可以通过 $\mathbf{v}$ 和 $\mathbf{n}$ 的方向来区分，详见后续普吕克坐标的计算）
   
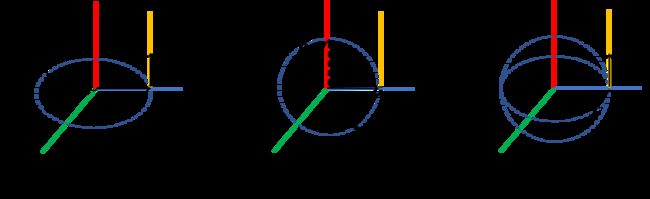
   若用直线上两个不同的点 $\mathbf{M}$ 和 $\mathbf{N}$ 来计算直线的方向向量和法向量，即 $\mathbf{v}=\mathbf{N}-\mathbf{M}$ 和 $\mathbf{n}=\mathbf{M}\times \mathbf{N}$，有 $||\mathbf{n}||=||\mathbf{M}||||\mathbf{N}||\sin \theta$，即 $n$ 的长度为两端点和原点构成的三角形的面积的2倍，$v$ 的长度又为该三角形底边长，因此 $d=\frac{||\mathbf{n}||}{||\mathbf{v}||}$，即 $d$ 的几何约束已经蕴含在了计算得到的方向向量 $\mathbf{v}$ 和法向量 $\mathbf{n}$ 中，由此实现了一条空间直线的唯一确定。

普吕克矩阵

普吕克矩阵广泛应用于直线的普吕克坐标的初始化中，定义为：
$${\mathbf{L}}^{\ast }=\left(\begin{array}{cc}[\mathbf{v}{]}_{\times }& \mathbf{n}\\ -{\mathbf{n}}^T& 0\end{array}\right)={\mathbf{X}}_1{\mathbf{X}}_2^T-{\mathbf{X}}_2{\mathbf{X}}_1^T\in {\mathbb{R}}^{4\times 4}$$其中，由于点和面的对偶性质，$X_1$ 和 $X_2$ 可以是线上两个端点 $M、N$ 的齐次坐标，也可以是两视图平面 ${\pi }_1、{\pi }_2$ 的齐次坐标，显然可以从普吕克矩阵中直接获得普吕克坐标。

普吕克矩阵具备特殊性质，它是一个对角线上元素皆为0的反对称矩阵，且行列式为0。若取同一空间直线上任意两对空间点，对应的普吕克坐标则只相差一个系数，即${\mathbf{L}}_1^{\ast }=\alpha {\mathbf{L}}_2^{\ast }$。因为反对称矩阵中有6个非零元素，但因为齐次坐标的关系仅有5个是有意义的，且由于存在行列式为0的正交约束，因此可反映出直线的自由度为4。

基于两端点的普吕克坐标表示方法

给定2个3D点 ${\mathbf{M}}^T=(\overline{\mathbf{M}},m{)}^T$ 和 ${\mathbf{N}}^T=(\overline{\mathbf{N}},n{)}^T$ ，6维向量的普吕克坐标 ${\mathbf{L}}^T=({\mathbf{n}}^T,{\mathbf{v}}^T{)}^T$ 表示如下：

$$\{\begin{array}{l}\mathbf{n}=\overline{\mathbf{M}}\times \overline{\mathbf{N}}\\ \mathbf{v}=(\frac{\overline{\mathbf{N}}}{n}-\frac{\overline{\mathbf{M}}}{m})\cdot mn=m\overline{\mathbf{N}}-n\overline{\mathbf{M}}\end{array}$$因此普吕克为6参数表示的5维齐次坐标系下的齐次表示，存在约束 ${\mathbf{n}}^T\mathbf{v}=0$，因此普吕克坐标表示的一条空间直线的自由度为5-1=4，符合直线自由度。

基于两平面的普吕克坐标表示方法

给定2个空间平面 ${\mathbf{P}}^T=(\overline{\mathbf{P}},p{)}^T$ 和 ${\mathbf{Q}}^T=(\overline{\mathbf{Q}},q{)}^T$ ，普吕克坐标如下：

$$\{\begin{array}{l}\mathbf{n}=(\frac{\overline{\mathbf{Q}}}{q}-\frac{\overline{\mathbf{P}}}{p})\cdot pq=p\overline{\mathbf{Q}}-q\overline{\mathbf{P}}\\ \mathbf{v}=\overline{\mathbf{P}}\times \overline{\mathbf{Q}}\end{array}$$对于法向量 $\mathbf{n}$ 的获取，假设两平面相交的直线上的一点 $X$，有$$\begin{array}{ccc}\{\begin{array}{l}\overline{\mathbf{P}}\mathbf{X}+p=0\\ \overline{\mathbf{Q}}\mathbf{X}+q=0\end{array}& \to \frac{\overline{\mathbf{Q}}}{q}\cdot X=\frac{\overline{\mathbf{P}}}{p}\cdot X& \to (p\overline{\mathbf{Q}}-q\overline{\mathbf{P}})\cdot X=0\end{array}$$可以看到两平面表示与两点表示的普吕克坐标表示方法呈现对偶形式。因此，两视图的直线三角化具备以下闭式解，给定 P${}^1$ 和 P ${}^2$ 两个投影矩阵，l${}^1$ 和 l${}^2$ 两条图像线，对应的3D空间线的普吕克坐标就可以表示为两个恢复的平面 ${\pi }^i\sim$ P${{}^i}^T$l${}^i$ 的相交。

投影模型和Camera-World转换

给定一个标准 $3\times 4$ 的透视投影矩阵 $P=(\overline{P},\mathbf{p})$，则可以在2D图像线和对应的3D空间线的普吕克坐标间建立关系式如下：$$\begin{array}{rl}{l}_{image}& =m_{image}\times n_{image}\\ & =(P\mathbf{M})\times (P\mathbf{N})\\ & =(\overline{P}\overline{\mathbf{M}}+m\mathbf{p})\times (\overline{P}\overline{\mathbf{N}}+n\mathbf{p})\\ & =(\overline{P}\overline{\mathbf{M}})\times (\overline{P}\overline{\mathbf{N}})+m\mathbf{p}\times (\overline{P}\overline{\mathbf{N}})-n\mathbf{p}\times (\overline{P}\overline{\mathbf{M}})+m\mathbf{p}\times n\mathbf{p}\\ & =det(\overline{P}){\overline{P}}^{-T}(\overline{\mathbf{M}}\times \overline{\mathbf{N}})+[\mathbf{p}{]}_{\times }\overline{P}(m\overline{\mathbf{N}}-n\overline{\mathbf{M}})\\ & =[det(\overline{P}){\overline{P}}^{-T},[\mathbf{p}{]}_{\times }\overline{P}]\left[\begin{array}{c}(\overline{\mathbf{M}}\times \overline{\mathbf{N}})\\ (m\overline{\mathbf{N}}-n\overline{\mathbf{M}}\end{array}\right]\\ & =\tilde{P}\mathbf{L}\end{array}$$
因此，普吕克坐标表示法中重投影图像线和3D空间线之间是线性转换关系。
$l_{image}$ 为相机坐标系下的直线法向量，$\mathbf{L}$ 为该直线在世界坐标系下的普吕克坐标。
根据上述推导可进一步的拓展出世界坐标系和相机坐标系之间的普吕克坐标的转换关系：$$\left[\begin{array}{c}{\mathbf{n}}_c\\ {\mathbf{v}}_c\end{array}\right]=\left[\begin{array}{cc}{\mathbf{R}}_{cw}& [{\mathbf{t}}_{cw}{]}_{\times }{\mathbf{R}}_{cw}\\ 0& {\mathbf{R}}_{cw}\end{array}\right]\left[\begin{array}{c}{\mathbf{n}}_w\\ {\mathbf{v}}_w\end{array}\right]=\left[\begin{array}{cc}{\mathbf{R}}_{wc}^T& {\mathbf{R}}_{wc}^T[{\mathbf{t}}_{cw}{]}_{\times }\\ 0& {\mathbf{R}}_{wc}^T\end{array}\right]\left[\begin{array}{c}{\mathbf{n}}_w\\ {\mathbf{v}}_w\end{array}\right]$$其中法向量的转换，将 $P$ 用 $\mathbf{R},\mathbf{t}$ 替换即可，方向向量的转换直接用 $\mathbf{R}$ 进行旋转。

2.3 其他的直线部分表示法

源于论文 Structure-From-Motion Using Lines: Representation, Triangulation and Bundle Adjustment 中提到的3种比较古旧的直线非完备表示法（不能表示所有直线），这里只做简单介绍。其实从最近的线SLAM工作也可以看出来，最常用的基本还是普吕克坐标表示（用于初始化 三角化）和正交参数表示（用于BA优化）。

最近点和方向

一条3D直线也可以用 1. 该直线离原点最近的点 ${\mathbf{Q}}^T=({\overline{\mathbf{Q}}}^T,1{)}^T$ 和 2. 该直线的方向 ${\mathbf{Q}}_{\infty }^T=({\overline{\mathbf{Q}}}_{\infty }^T,0{)}^T$ （逆深度为0表示的即为方向向量）来表示，共计6个参数。显然该直线表示法不能表示那些位于无穷远处的直线（无最近点）。

• 与普吕克坐标的转换关系
  
• 重投影公式
  
  显然为双线性函数。

两投影线

一条3D直线也可以用两次投影来表示，因为两视图的直线恢复具备唯一解。注意这里的“两投影”，指的是3D直线在对应正交平面的投影线。
已知一条3D直线可以用两个平面的相交来表示，指定这两个平面中， ${\pi }_1$ 平行于 $x$ 轴，${\pi }_2$ 平行于 $y$ 轴，则可以用 ${\pi }_1$ 和 ${\pi }_2$ 的相交去表示所有非平行于 $XY$ 平面（或者说垂直于 $z$ 轴）的空间3D直线。

• 其中 ${\pi }_2$ 与 $y=0$ 平面的相交也就是该空间直线在 $y=0$ 平面的投影线，用 $x=az+b$ 表示。
• 同样 ${\pi }_1$ 与 $x=0$ 平面的相交也就是该空间直线在 $x=0$ 平面的投影线，用 $y=cz+d$ 表示。

如图所示

其中直线过 $XY$ 平面的交点为 $(b,d,0)$ ，方向向量为 $(a,c,1)$，结合两条投影线和 $z$，可将直线上任一点表示为 $Q=\left(\begin{array}{c}az+b\\ cz+d\\ z\\ 1\end{array}\right)$，该表示法为4参数表达，但显而易见的存在奇点(singularities) : 无法表示平行于 $z=0$ 平面的直线。即使选取不同的参考轴和参考平面，始终无法完备表示所有直线。

• 与普吕克坐标的转换关系
  任意选取线上两点即可，如 $z=0$ 和 $z=1$，即有 $L=\left(\begin{array}{c}d\\ -b\\ bc-da\\ a\\ c\\ 1\end{array}\right)$。
• 重投影公式
  同样为双线性函数。

Denavit–Hartenberg 参数

也就是机械工程中常用的D-H参数表示，核心思想是设置世界坐标系为参考坐标系，将其 $z$ 轴视作固定的一个机械关节，将空间直线视为另一个可动机械关节并对齐所在坐标系的 $z$ 轴，并令所在坐标系的 $x$ 轴为参考坐标系和直线所在坐标系的 $z$ 轴的公共法线，由此就将原本 6 自由度的位姿变换缩减了 2 个自由度（沿轴平移和绕轴旋转），示意图如下所示：

其中包括两个角度、两个距离，这里我们将图中连接两个关节的s型连接称作连杆：

• $\alpha$ : 连杆转角，直线所在坐标系的 $z$ 轴与世界坐标系的 $z$ 轴之间绕直线所在坐标系 $x$ 轴的转角。
• $\theta$：关节转角，直线所在坐标系的 $x$ 轴与世界坐标系的 $x$ 轴之间绕直线所在坐标系 $z$ 轴的转角。
• $d$：连杆偏移，直线所在坐标系的 $x$ 轴与世界坐标系的 $x$ 轴之间沿直线所在坐标系 $z$ 轴的位置偏移。
• $a$：连杆长度，直线所在坐标系的 $z$ 轴与世界坐标系的 $z$ 轴之间沿公共法线（直线所在坐标系 $x$ 轴）的位置偏移。

这种表示法当然也存在着限制：a) 由于涉及到了两个距离参数，因此不能表示在无穷远处的直线；b) 同时，也不能表示垂直于参考坐标系的 $z$ 轴的直线。

• 与普吕克坐标的转换关系
  将该4参数表示的坐标系变换，作用到世界坐标系下 $z$ 轴的普吕克坐标 $L_z^T=(000001{)}^T$ 上。
• 重投影公式
  其中包含乘积和三角函数，因此也是非线性的，不再赘述。

2.4 正交表示 (Orthonormal Representation)

普吕克坐标虽然能完备的表示所有空间直线，且重投影函数为线性，但本身的6个参数却不是线特征的最小表示（4参数），包含了内在约束 $n^{T}v=0$。对3D空间直线的过参数化表示可能会带来以下问题：

• 多余的参数会增加每次迭代的计算代价
• 内在约束会带来优化过程中的数值不稳定性。

在这种情况下，正交表示可以说为非线性BA优化而生。用与空间直线自由度匹配的最小4个参数来表示，给优化过程带来了便利。因此，在现在众多基于贺博的PL-VIO框架的经典工作中，正交表示法成为了优化过程中残差计算的普遍选择。

正交表示推导

假设一条3D直线的普吕克坐标为 ${\mathbf{L}}^T=({\mathbf{n}}^T,{\mathbf{v}}^T{)}^T$，写作矩阵形式为 ${\mathbf{C}}_{3\times 2}=(\mathbf{n},\mathbf{v})$，将矩阵 $\mathbf{C}$ 进行QR分解后重新表示为 ${\mathbf{C}}_{3\times 2}=({\mathbf{U}}_{3\times 3},{\mathbf{\Sigma }}_{3\times 2})$，即：
$$\begin{array}{c}\mathbf{C}=\left(\begin{array}{c}\frac{\mathbf{n}}{||\mathbf{n}||}\frac{\mathbf{v}}{||\mathbf{v}||}\frac{\mathbf{n}\times \mathbf{v}}{||\mathbf{n}\times \mathbf{v}||}\end{array}\right)\\ SO(3)\end{array}\begin{array}{c}\left(\begin{array}{cc}||\mathbf{n}||& 0\\ 0& ||\mathbf{v}||\\ 0& 0\end{array}\right)\\ (||\mathbf{n}||,||\mathbf{v}||{)}^T\in {\mathbb{P}}^1\end{array}$$其中，

• ${\mathbf{U}}_{3\times 3}$ 为第一部分的正交旋转矩阵，自由度为3。
• ${\mathbf{\Sigma }}_{3\times 2}$ 为第二部分的上三角矩阵，由两个标量组成，其中 $(||\mathbf{n}||,||\mathbf{v}||)$ 为一维齐次坐标表示，自由度为1。
• ${\mathbf{\Sigma }}_{3\times 2}$ 中第一行第二列元素（右上角）必定为0，因为普吕克坐标存在约束 ${\mathbf{n}}^T\mathbf{v}=0$。
• ${\mathbf{\Sigma }}_{3\times 2}$ 中同时除以 $||v||$ 可得 $d=\frac{||\mathbf{n}||}{||\mathbf{v}||}$，因此其中包含了直线到原点的距离信息。

为了方便进行优化和更新，将 $\mathbf{\Sigma }$ 进一步以 $(2\times 2)$ 的 $SO(2)$来表示如下：$$\mathbf{W}=\frac{1}{\sqrt{1+d^2}}\left[\begin{array}{cc}d& -1\\ 1& d\end{array}\right]=\frac{1}{\sqrt{||\mathbf{n}||+||\mathbf{v}||}}\left[\begin{array}{cc}||\mathbf{n}||& -||\mathbf{v}||\\ ||\mathbf{v}||& ||\mathbf{n}||\end{array}\right]=\left[\begin{array}{cc}\cos (\varphi )& -\sin (\varphi )\\ \sin (\varphi )& \cos (\varphi )\end{array}\right]=\left[\begin{array}{cc}w1& -w2\\ w2& w1\end{array}\right]\in SO(2)$$

综上所述，直线的正交表示可以写作：
$$\mathbf{C}=(\mathbf{U},\mathbf{W})\in SO(3)\times SO(2)$$

• 与普吕克坐标的转换关系

正交表示可以最小的表示直线，但是该表示方法的投影方程并没有线性的表示，即该方法并不能像Plucker坐标系表示方法一样，通过公式$$\left[\begin{array}{c}{\mathbf{n}}_c\\ {\mathbf{v}}_c\end{array}\right]=\left[\begin{array}{cc}{\mathbf{R}}_{cw}& [{\mathbf{t}}_{cw}{]}_{\times }{\mathbf{R}}_{cw}\\ 0& {\mathbf{R}}_{cw}\end{array}\right]\left[\begin{array}{c}{\mathbf{n}}_w\\ {\mathbf{v}}_w\end{array}\right]=\left[\begin{array}{cc}{\mathbf{R}}_{wc}^T& {\mathbf{R}}_{wc}^T[{\mathbf{t}}_{cw}{]}_{\times }\\ 0& {\mathbf{R}}_{wc}^T\end{array}\right]\left[\begin{array}{c}{\mathbf{n}}_w\\ {\mathbf{v}}_w\end{array}\right]$$得到一个线性的映射关系，但是我们又特别的看重该表示方法的最小表示的性质，好在两者之间的互换关系还是十分简单的，如下

（引用于 SLAM线特征学习（1）——基本的线特征表示与优化推导）

在SLAM中，世界坐标系和相机坐标系的线特征转换是非常频繁且重要的。因此在很多经典框架中，一般在直线的初始化和线特征容器中使用普吕克坐标表示，在进行非线性BA优化的时候，求取观测残差最终对正交表示的4个参数 $(\mathbf{\theta },\varphi )$ 的Jacobian矩阵并进行参数的优化更新：$\mathbf{U}\leftarrow \mathbf{U}\cdot \mathrm{R}(\mathrm{\Delta }\mathbf{\theta })$ ，$\mathbf{W}\leftarrow \mathbf{W}\cdot \mathrm{R}(\mathrm{\Delta }\varphi )$，最后对相应3D空间直线的普吕克坐标进行更新。

详细的线段观测的重投影误差对相机姿态、相机平移和直线参数的Jacobian 推导仍然可见 SLAM线特征学习（1）——基本的线特征表示与优化推导，这里不再赘述。

---

3. 结构信息约束下的线特征表示 —— 2-DoF表示

在实际应用中，人工环境由于存在大量规则的、结构化的线条，线特征不是无意义的分布在空间中，而是呈现一定的规律：如沿着固定的主方向 (dominant direction，常规的方正建筑环境下为3个互相垂直的方向），相互垂直或平行等，因此在对应的Manhattan世界假设或者Atlanda世界假设下，3D空间直线可以存在更简练的表示方法，这就是一脉相承的 2-DoF 线表示法。

3.1 StructSLAM : Visual SLAM with Building Structure

邹丹平老师组的经典工作，提出了一种新颖的在Manhattan世界假设下的结构线表示方法。

结构线参数化表示方法

原文翻译>如图所示，选择世界坐标系下的三个正交平面($XY、YZ、ZX$)为参数平面，用来对三种属于不同主方向的结构线进行更凝练的参数化表示，以 $XZ$ 平面为例，一条结构线可以用为过参数平面 $XZ$ 的点 $A$ 和其所属的主方向 $\eta$ 来表示。选择直线所属主方向和三种平面的法向量的角度偏差最小的那个为参数平面。采用逆深度表示法，一条结构线就可以表示如下：$$\mathbf{l}={\left(\begin{array}{c}{c}_a,c_b,\theta ,h\end{array}\right)}^T$$其中，

• $(c_a,c_b{)}^T$ 为相机光心 $O$ 沿着主方向 $\eta$ 在参数化平面上的投影点 $O^{\prime }$的坐标。
• $\theta$ 为参数平面交点 $A$ 到 $O^{\prime }$的 射线在参数平面上的角度。
• $h$ 为参数平面交点 $A$ 到 $O^{\prime }$的逆深度。

虽然对结构线采用了4个参数的表示方法，但只要确定了对应的参数平面，本质上就只取决于点 $A$ 的位置，即只具备其对应的参数平面上的2个自由度。世界坐标系下的线特征的空间表示很明显不应受相机位姿的影响，因此这种表示方法只能建立在相机位姿和正确识别对应参数平面的先验信息上。

结构线初始化方法

原文翻译

• 第一步，计算相机中心沿着该条直线所属的主方向在参数平面的投影，即 $(c_a,c_b)$。
• 第二步，获取相机中心投影到直线在参数平面交点的方向，即 $(\cos \theta ,\sin \theta )$。
• 结构线的状态初始化为 $\mathbf{l}=(c_a,c_b,\theta ,h{)}^T$，对于 $h$ 先设置一个初始值，等待后续优化更新。

详细的初始化过程为：

1. 假设线段中点的 $3\times 1$ 的齐次坐标为 $\tilde{m}$，则世界坐标系下的3D坐标计算如下：$$\mathbf{m}={\mathbf{R}}^{wc}{\mathbf{K}}^{-1}\tilde{\mathbf{m}}+{\mathbf{p}}^w$$则该直线在世界坐标系下的普吕克矩阵为：$${\mathbf{L}}^{\ast }=\mathbf{m}{\eta }^T-\eta {\mathbf{m}}^T$$其中 $\eta \in {\mathbb{R}}^{3\times 1}$ 为对应的主方向。
   ( 基于点的普吕克矩阵计算，只不过其中一个点的齐次坐标逆深度为0，即本质为一条射线 )
2. 计算该结构线与对应参数平面 $\pi$的交点 $A$ 的坐标如下：$${\tilde{\mathbf{l}}}^w={\mathbf{L}}^{\ast }\pi$$参数平面的2D坐标计算为：$${\mathbf{l}}^p=\mathbf{P}{\mathbf{l}}^w$$其中 ${\mathbf{l}}^w$ 为齐次坐标形式的 ${\tilde{\mathbf{l}}}^w$ 对应的3D坐标, $\mathbf{P}\in {\mathbb{R}}^{2\times 3}$ 为从世界坐标系到2D参数平面的投影转换矩阵。
   同样的方法获取相机中心沿着主方向在参数平面的投影 $O^{\prime }$。
   $${\tilde{\mathbf{o}}}^w=(\mathbf{c}{\eta }^T-\eta {\mathbf{c}}^T)\pi$$则2D投影坐标为：$${\mathbf{o}}^p=\mathbf{P}{\mathbf{o}}^w$$
3. 初始化结构线为：$$\mathbf{l}=[c_a,c_b,\theta ,h{]}^T=[{\mathbf{o}}^p(1),{\mathbf{o}}^p(2),\arctan (\frac{{\mathbf{l}}^p(2)-{\mathbf{o}}^p(2)}{{\mathbf{l}}^p(1)-{\mathbf{o}}^p(1)}),h_0{]}^T$$，其中 $h_0$ 为预设的逆深度初始值。

结构线重投影方法

原文翻译
根据参数平面的投影关系，得到线段中点在世界坐标系下的坐标为$${\mathbf{l}}^w={\mathbf{P}}^T([c_a,c_b{]}^T+[\cos \theta ,\sin {\theta }^T]/h)$$两边同时乘上 $h$ 以应对无限远的情况，有
$${\mathbf{l}}^{w}h={\mathbf{P}}^T([c_a,c_b{]}^{T}h+[\cos \theta ,\sin {\theta }^T])$$其中$\mathbf{P}\in {\mathbb{R}}^{2\times 3}$，减去相机中心的世界坐标获得相机坐标系的空间齐次坐标$${\mathbf{l}}^c={\mathbf{R}}^{cw}{\mathbf{l}}^{w}h-{\mathbf{R}}^{cw}{\mathbf{p}}^{w}h$$和像素坐标$${\mathbf{l}}^i=\mathbf{K}{\mathbf{l}}^c$$ 则结构线的投影方程(法向量）即为$$\overline{\mathbf{l}}=\mathbf{v}\times {\mathbf{l}}^i$$其中 $v$ 为灭点的齐次坐标。

3.2 StructVIO : Visual-inertial Odometry with Structural Regularity of Man-made Environments

邹丹平老师组在结构线SLAM的进一步工作，这次不仅仅是Manhattan Wold假设了，而是更进一步的Atlanta World假设（有着不同水平方向 ${\varphi }_i\in [0,\pi /2]$的Manhattan世界的集合），更为普适通用，如下：

在结构线的一系列处理上和StructSLAM相比也有区别，详见后文。

结构线参数化表示方法

注意红色标注部分与StructSLAM的一致性。

原文翻译(1)

• 每条结构线都会被锚定在第一次被观测到的图像帧下的局部坐标系上，称作起始帧 $\{S\}$，该局部坐标系的方向与该结构线所属的Manhattan世界的方向 ${\varphi }_i$一致，原点即为该图像帧的相机位置 ${}^W{p}_S$，且 ${}^W{p}_S$ 将加入状态向量进行更新维护。这里将设置一个虚拟的Manhattan世界 ${\varphi }_0$，与世界坐标系 $W$ 的方向一致，则 ${\varphi }_i$ 即为相对于世界坐标系的水平方向偏差。
• 对每条结构线都可以找到一个从参数空间 $\{L\}$到起始帧$\{S\}$的旋转矩阵 ${}_L^{S}R$，其中，结构线会与$\{L\}$的 $Z$ 轴对齐，如下图所示：
  
  在参数空间中，每条结构线都可以简单的用其与$XY$平面的交点（显然仍为2自由度）来表示，即为 ${}^L{l}_p=(a,b,0{)}^T$。这里我们将其转化为逆深度表示法，即为 ${}^L{l}_p=(\theta ,\rho ,0{)}^T$，其中 $\rho =1/\sqrt{a^2+b^2}$，$\theta =\arctan (b,a)$。逆深度表示法的优点已经多次阐述：1. 可以描述无穷远的特征。2.减少特征初始化的非线性。
• 因此，该结构线在起始帧的坐标可以计算如下$$\begin{array}{rl}{}_L^{S}R{}^L{l}_p& =a_L^{S}R(:,1)+b_L^{S}R(:,2)+0{\cdot }_L^{S}R(:,2)\\ & =\frac{\cos \theta }{\rho }{}_L^{S}R(:,1)+\frac{\sin \theta }{\rho }{}_L^{S}R(:,2)\end{array}$$无论该结构线对齐到当前局部坐标系的任意一轴，都可以用下列三个矩阵来表示 ${}_L^{S}R$

这里作一下解释，这里参数平面的选取本质上和StructSLAM是一样的，只不过统一使结构线对齐到参数空间 $L$ 的$Z$ 轴，同时对参数空间到局部Manhattan坐标系的转换 ${}_L^{S}R$ 做了具体的直观展示，从而将三个空间 $\{L\}$、$\{S\}$、$\{C\}$联系在一起（其中起始帧 $S$ 所在的局部Manhattan坐标系，其实和世界坐标系只差一个方向 ${\varphi }_i$ 的区别），论文里的这张图就个人感觉来说不是那么直观，我重新画的示意图如下：

没有把相机坐标系画进去是避免产生误解，且更便于直观理解$\{L\}$ 到 $\{S\}$的旋转关系，建议这里直接把 $\{S\}$ 理解成真实世界的坐标指向，则结构线可能属于 $XYZ$ 三个主方向中的其中一个，将对应的参数平面贴上去即可。

原文翻译(2)

• 从起始坐标系 $\{S\}$ 到 世界坐标系的旋转矩阵为 ${}_S^{W}R({\varphi }_i)$，只与绕重力方向的水平偏角 ${\varphi }_i$有关，因此表示如下
  对于竖直方向的结构线，统一令其起始帧坐标系与世界坐标系的方向一致，也就是 ${}_S^{W}R=={}_S^{W}R({\varphi }_0)=I_{3\times 3}$。

结构线重投影方法

原文翻译(1)
为了获取结构线在图像上的投影，需要同时将交点 ${}^{L}lp$ 和 参数平面的 $z$ 轴方向（其实就是获取灭点）投影到图像平面上。其中${}^{L}lp$ 在世界坐标系下的坐标计算如下：$${}^W{l}_p={}_S^{W}R({\varphi }_i){}_L^{S}R{}^L{l}_p+{}^W{p}_S$$进一步转换到相机坐标系下 $${}^C{l}_p={}_W^{C}R{}^W{l}_p+{}^C{p}_W$$将${}^{L}lp$ 用逆深度表示法替换，则可得到$${}^C{l}_p\sim {}_W^{C}R{}_S^{W}R({\varphi }_i){}_L^{S}R\cdot r+({}_W^{C}R{}^W{p}_S+{}^C{p}_W)\cdot \rho$$其中 $r=[\cos \theta ,\sin \theta ,0{]}^T$，参数空间的 $Z$ 轴方向投影出的灭点的齐次坐标也可计算如下$${}^{C}v\sim {}_W^{C}R{}_S^{W}R({\varphi }_i){}_L^{S}R(:,3)$$考虑内参矩阵，则可以得到图像中的直线方程（法向量）如下：$${}^{im}l=(K^{-T})({}^C{l}_p\times {}^{C}v)$$

这里其实可以看到与StructSLAM对结构线参数化表示的本质一致性，都是用角度 $\theta$ 和 逆深度 $\rho$ 对结构线与参数平面交点的重新表示，将灭点和参数平面交点重投影回图像平面，叉乘获取直线方程。

结构线初始化方法

原文翻译
初始化一条新的结构线$l=(\theta ,\rho )$的关键在于找到角度参数 $\theta$，逆深度 $\rho$ 可以先取预设的一个值。

1. 给结构线建立一个起始坐标系。竖直线都令其起始坐标系与世界坐标系对齐；对于水平方向的结构线，令其起始坐标系为偏角为 ${\varphi }_i$ 的局部manhattan坐标系。
2. 角度参数 $\theta$ 取决于在$XY$平面上的相机中心到结构线的方向。这个方向可以近似为从相机中心到线段中点的射线方向。让 $m$ (齐次坐标形式）为观测线段 $s$ 的中点，投影到参数平面：$${}^{L}m={}_S^{L}R{}_W^{S}R({\varphi }_i){}_C^{W}R{K}^{-1}m$$角度 $\theta$ 计算为${\theta }_0=\arctan (m_y,m_x)$，其中 ${}^{L}m=(m_x,m_y,m_z{)}^T$，将这个过程概括为:$$l_0=\left(\begin{array}{c}{\theta }_0\\ {\rho }_0\end{array}\right)=\left(\begin{array}{c}{\Pi }^{-1}(s,{\varphi }_i,{}_C^{W}R)\\ {\rho }_0\end{array}\right)$$

与StructSLAM相比，每一条结构线都被锚定在了第一次观测的相机帧上，并且和该帧相机的位姿建立了联系，参数平面、起始坐标系、相机坐标系的原点都为起始帧的相机位置，相互之间只需要进行旋转变换即可，不需要将相机中心再向参数平面投影了，进一步简化和规范化了参数化表示的流程。

当然本质基本不变： 在结构信息和相机位姿的约束下，每条结构直线可以只用2个自由度的参数平面来进行表示。

3.3 Leveraging Structural Information to Improve Point Line Visual-Inertial Odometry

对结构线和非结构性都能用两个参数进行表示，思路和StructSLAM、StructVIO相似，作者有一个开源的4参数和2参数线优化的仿真代码，在速度精度上确实有提升，代码解析可参考上一篇博客 PLS-VIO代码解读，

非结构线参数化表示方法

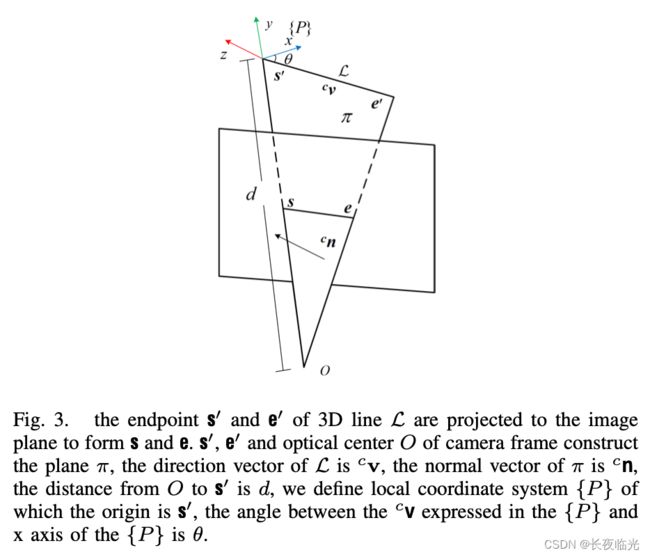
一条空间直线可以表示为普吕克坐标： $\mathcal{L}={[}^c{\mathbf{n}}^T,{{}^c\mathbf{v}}^T{]}^T$，因直线位于相机与直线构成的平面 $\pi$ 上，因此基于相同的思路将平面 $\pi$ 视为参数平面，建立一个局部坐标系 $\{P\}$：

• 坐标系原点设置为3D空间线段的端点 $s^{\prime }$
• $y$轴方向与相机中心到端点 $s$ 的射线对齐，$z$轴方向与 $\pi$ 的正交向量 ${}^c\mathbf{n}$ 平行，$x$轴方向与 $y$ 轴 和 $z$ 轴垂直。

从相机中心 $O$ 到端点 $s^{\prime }$ 的距离为 $d$，用逆深度表示为 $\rho =1/d$，并且令 $\theta$ 为局部坐标系下的直线方向 ${}^c{\mathbf{v}}^{\prime }$ 与 $x$ 轴之间的偏角，其中 ${}^c{\mathbf{v}}^{\prime }={\mathbf{R}}_C^P{}^c\mathbf{v}$。因此，在局部参数坐标系$\{P\}$下就将一条非结构线也用两个参数进行了表示，在线特征的优化过程中可以减少线段参数数量，是一种更紧凑的表达方法。

非结构线初始化方法

原文翻译
在归一化相机平面的线段观测可以用两个端点坐标表示： ${\mathbf{s}}^{c_1}=[u_s,v_s,1{]}^T$ 和 ${\mathbf{e}}^{c_1}=[u_e,v_e,1{]}^T$，三点确定一个平面，加上相机中心 $O$ 即可确定平面 $\mathbf{\pi }=[{\pi }_x,{\pi }_y,{\pi }_z,{\pi }_w]$，给定相机坐标系 $c_1$ 下的两个平面 ${\mathbf{\pi }}_1$ 和 ${\mathbf{\pi }}_2$，则可获取普吕克矩阵 ${}^c{\mathcal{L}}^{\ast }$如下:

从${}^c{\mathcal{L}}^{\ast }$中可获取相应的$c_1$下的普吕克坐标 ${}^c\mathcal{L}$，然后将 ${}^c\mathbf{v}$ 从相机坐标系旋转到局部坐标系$\{P\}$下：$${}^c{\mathbf{v}}^{\prime }=R_C^P{}^c\mathbf{v}$$其中 $R_C^P$ 的列显然由局部坐标系$\{P\}$的 $x,y,z$轴（也就是这三个轴方向在$c_1$下的坐标）构成。因此我们可以初始化参数 $\theta$ 为 $x$ 轴与${}^c{\mathbf{v}}^{\prime }$之间的角度，其中 $\rho$ 可以预设为一个默认值 ${\rho }_0=0.2$。

非结构线重投影方法

原文翻译
局部参数坐标系下的直线方向向量（注意与结构线区分）计算如下：${}^d\mathbf{v}=[\cos \theta ,\sin \theta ,0{]}^T$，因此我们可以将 ${}^d\mathbf{v}$ 从参数坐标系转换到相机坐标系来获取 ${}^c\mathbf{v}$：$${}^c\mathbf{v}={\mathbf{R}}_P^C{}^d\mathbf{v}$$其中一个端点 $\mathbf{s}$在相机坐标系下的坐标计算为：$$\mathbf{s}=\frac{\mathbf{y}}{||\mathbf{y}||}\cdot d$$其中 $\mathbf{y}$ 为局部坐标系的 $y$ 轴。
为了获得在归一化相机坐标系下的直线投影，需要将起始相机坐标系下的端点 $\mathbf{s}$ 和 方向向量 ${}^c\mathbf{v}$ 转换到目标坐标系下：

其中 $({\mathbf{R}}_{C_i}^W,{\mathbf{P}}_{C_i}^W)$ 为第一次观测到该直线的相机关键帧。则直线投影方程可以直接获得如下:$${\mathbf{l}}_l^{m_i}=[{\mathbf{s}}^{\prime }{]}_{\times }{}^c{\mathbf{v}}^{\prime }$$

结构线参数化表示方法

与StructVIO完全一致，用 ${\mathbf{l}}_p^l=[\theta ,\rho ,0{]}^T$ 来表示。

结构线初始化方法

原文翻译
结构线的初始化同样需要首先计算普吕克坐标${}^c\mathcal{L}={[}^c{\mathbf{n}}^T{,}^c{\mathbf{v}}^T{]}^T$，然后我们通过line triming方法(结合相机位姿)来获得该直线在世界坐标系下的端点坐标 ${}^w\mathcal{L}=[{\mathbf{s}}^{wT},{\mathbf{e}}^{wT}{]}^T$。为了获取直线${}^w\mathcal{L}$与 $XY$ 平面在世界坐标系下的交点，将齐次坐标表示的参数平面 ${}^l\mathbf{p}$ 转移到世界坐标系下：
结合 ${}^w\mathcal{L}$ 和 ${}^w\mathbf{p}$即可获得在世界坐标系下的交点 ${}^w{\mathbf{l}}_p$，反过来重新转换到参数空间后即可得到参数空间下的交点${}^l{\mathbf{l}}_p$：

根据参数空间的交点坐标 ${[}^{l}lpx{,}^{l}lpx,0]$ 即可实现对 $\theta$ 和 $\rho$的初始化。

这里对结构线初始化的操作和StructSLAM是一样的，都是在世界系下求出直线和参数平面的交点坐标，再转换回参数空间，而StructVIO则是直接投影空间直线的中点回到参数平面上，本质上是一样的。

结构线重投影方法

与StructVIO一致，不再赘述。