机器学习-聚类算法-02

聚类算法实践

1. Kmeans

1. 导包操作

   导入numpy、matplotlib工具包，以及画图操作的相关参数设置，最后导入的包是防止环境出现警告

import numpy as np
import os
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt

plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12

import warnings
warnings.filterwarnings('ignore')
np.random.seed(42)

2. 绘制中心点并设置发散程度

# 导入绘制类别的工具包
from sklearn.datasets import make_blobs

# 指定五个中心点
blob_centers = np.array(
[
    [0.2,2.3],
    [-1.5,2.3],
    [-2.8,1.8],
    [-2.8,2.8],
    [-2.8,1.3]
]
)

# 五个点对应的发散程度,应当设置的小一点
blob_std = np.array([0.4,0.3,0.1,0.1,0.1])

3. 设置样本

# 参数n_samples：样本个数，centers：样本中心点,cluster_std:以中心点为圆心，向周围发散的程度
X,y = make_blobs(n_samples = 2000,centers=blob_centers,cluster_std=blob_std,random_state=7)

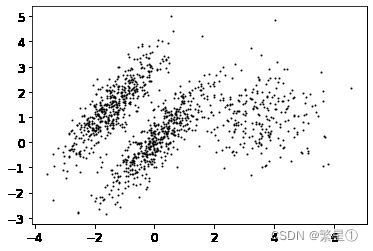
4. 画图展示

def plot_clusters(X,y = None):
    plt.scatter(X[:,0],X[:,1],c=y,s=1)
    plt.xlabel("$x_1$",fontsize=14)
    plt.ylabel("$x_2$",fontsize=14,rotation=0)
    
plt.figure(figsize=(8,4))
# 无监督学习，传递参数的时候只传递X值
plot_clusters(X)
plt.show()

5. 效果展示
   

2. 决策边界

1. 假定k=5进行分类

from sklearn.cluster import KMeans
k = 5
kmeans = KMeans(n_clusters = 5,random_state = 42)
# 计算聚类中心并预测每个样本的聚类索引
# fit_predict(X)与kmeans.labels_得到的结果是一致的
y_pred = kmeans.fit_predict(X)

2. 画图展示

# 把当前的数据进行展示
def plot_data(X):
    plt.plot(X[:, 0], X[:, 1], 'k.', markersize=2)

# 绘制中心点
def plot_centroids(centroids, weights=None, circle_color='w', cross_color='k'):
    if weights is not None:
        centroids = centroids[weights > weights.max() / 10]
    plt.scatter(centroids[:, 0], centroids[:, 1],
                marker='o', s=30, linewidths=8,
                color=circle_color, zorder=10, alpha=0.9)
    plt.scatter(centroids[:, 0], centroids[:, 1],
                marker='x', s=50, linewidths=5,
                color=cross_color, zorder=11, alpha=1)

# 绘制等高线
def plot_decision_boundaries(clusterer, X, resolution=1000, show_centroids=True,
                             show_xlabels=True, show_ylabels=True):
    mins = X.min(axis=0) - 0.1
    maxs = X.max(axis=0) + 0.1
    # 棋盘操作
    xx, yy = np.meshgrid(np.linspace(mins[0], maxs[0], resolution),
                         np.linspace(mins[1], maxs[1], resolution))
    # 预测结果值          合成棋盘
    Z = clusterer.predict(np.c_[xx.ravel(), yy.ravel()])
    # 预测结果值与棋盘一致
    Z = Z.reshape(xx.shape)
    
    # 绘制等高线，并绘制区域颜色
    plt.contourf(Z, extent=(mins[0], maxs[0], mins[1], maxs[1]),
                cmap="Pastel2")
    plt.contour(Z, extent=(mins[0], maxs[0], mins[1], maxs[1]),
                linewidths=1, colors='k')
    plot_data(X)
    
    if show_centroids:
        plot_centroids(clusterer.cluster_centers_)

    if show_xlabels:
        plt.xlabel("$x_1$", fontsize=14)
    else:
        plt.tick_params(labelbottom='off')
        
    if show_ylabels:
        plt.ylabel("$x_2$", fontsize=14, rotation=0)
    else:
        plt.tick_params(labelleft='off')
        

 
# 调用函数开始绘图
plt.figure(figsize = (8,4))
plot_decision_boundaries(kmeans,X)
plt.show()

3. 效果展示
   

3. 算法流程

​ 就是看程序每一步的优化结果

1. 设置优化步数

# max_iter设置1/2/3相当于三步
kmean_iter1 = KMeans(n_clusters=5,init='random',n_init=1,max_iter=1,random_state=1)
kmean_iter2 = KMeans(n_clusters=5,init='random',n_init=1,max_iter=2,random_state=1)
kmean_iter3 = KMeans(n_clusters=5,init='random',n_init=1,max_iter=3,random_state=1)

kmean_iter1.fit(X)
kmean_iter2.fit(X)
kmean_iter3.fit(X)

2. 画图展示

plt.figure(figsize=(12,10))
plt.subplot(321)
# 绘制初始点
plot_data(X)
# 绘制中心点
plot_centroids(kmean_iter1.cluster_centers_, circle_color='r', cross_color='k')
plt.title('Update cluster_centers')

plt.subplot(322)
plot_decision_boundaries(kmean_iter1, X,show_xlabels=False, show_ylabels=False)
plt.title('Iter1')

plt.subplot(323)
plot_decision_boundaries(kmean_iter1, X,show_xlabels=False, show_ylabels=False)
plot_centroids(kmean_iter2.cluster_centers_,circle_color='r',cross_color='g')
plt.title('Change1')

plt.subplot(324)
plot_decision_boundaries(kmean_iter2, X,show_xlabels=False, show_ylabels=False)
plt.title('Iter2')

plt.subplot(325)
plot_decision_boundaries(kmean_iter2, X,show_xlabels=False, show_ylabels=False)
plot_centroids(kmean_iter3.cluster_centers_,circle_color='r',cross_color='g')
plt.title('Change2')

plt.subplot(326)
plot_decision_boundaries(kmean_iter3, X,show_xlabels=False, show_ylabels=False)
plt.title('Iter3')

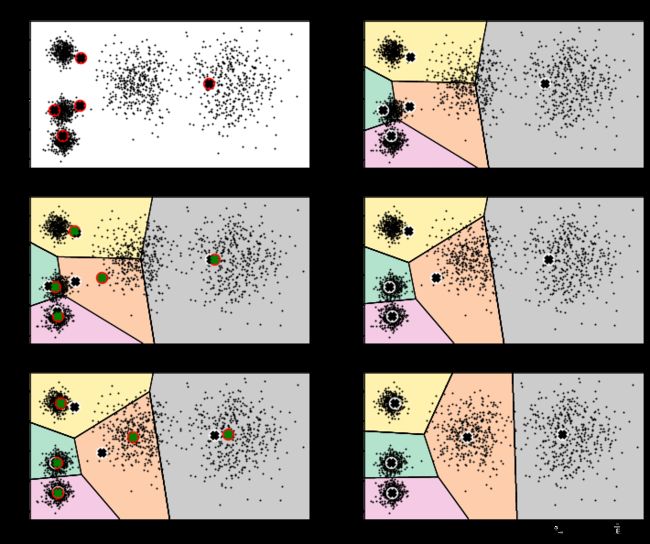
3. 效果展示
   图1为最开始的数据和生成的随机点分布；图2开始进行第一次迭代；图3是进行第二次迭代的过程，其中，黑白点代表上一次中心点的位置，红绿点代表本次迭代后中心点的更新；图4是第二次迭代后的中心点的位置；图5和图6分别是第三次迭代过程和结果中心点的分布情况。
   

4. 不稳定的结果

1. 画图展示

def plot_clusterer_comparison(c1,c2,X):
    c1.fit(X)
    c2.fit(X)
    
    plt.figure(figsize=(12,4))
    plt.subplot(121)
    plot_decision_boundaries(c1,X)
    plt.subplot(122)
    plot_decision_boundaries(c2,X)
    
    
    
# 创建对象，进行不同(质心初始化的随机数生成)结果对比 
c1 = KMeans(n_clusters = 5,init='random',n_init = 1,random_state=11)
c2 = KMeans(n_clusters = 5,init='random',n_init = 1,random_state=19)
plot_clusterer_comparison(c1,c2,X)

2. 效果展示

   不同的质心初始化的随机数生成次数，得到的结果是不稳定的

5. 评估方法

Inertia指标：每个样本到它最近簇的距离的平方和然后求和

kmeans.inertia_
## 211.5985372581684

X_dist = kmeans.transform(X)
# 找到每个样本到最近的簇的距离
X_dist[np.arange(len(X_dist)),kmeans.labels_]

np.sum(X_dist[np.arange(len(X_dist)),kmeans.labels_]**2)
## 211.59853725816868

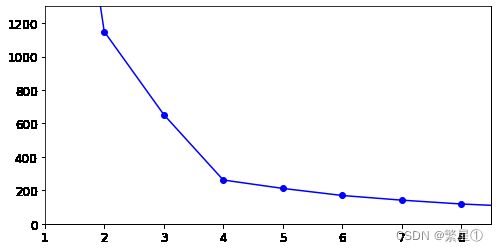
6. 找到最佳簇数

1. 选择10次数据进行查找

kmeans_per_k = [KMeans(n_clusters = k).fit(X) for k in range(1,10)]
inertias = [model.inertia_ for model in kmeans_per_k]

2. 画图展示

plt.figure(figsize=(8,4))
plt.plot(range(1,10),inertias,'bo-')
plt.axis([1,8.5,0,1300])
plt.show()

3. 效果展示

   根据下图所示，横轴为4的时候出现拐点，意思就是根据Inertia指标评估出来的簇的个数为4，但是肉眼可见应当是5个簇比较合理，所以Inertia指标只能作为参考
   

7. 轮廓系数

结论：

• s(i)接近1，则说明样本(i)聚类合理；
• s(i)接近-1，则说明样本(i)更应该分类到另外的簇；
• 若s(i) 近似为0，则说明样本(i)在两个簇的边界上。

1. 计算所有样本的平均轮廓系数

from sklearn.metrics import silhouette_score
# 计算所有样本的平均轮廓系数
silhouette_score(X,kmeans.labels_)

2. 计算所有轮廓系数

silhouette_scores = [silhouette_score(X,model.labels_) for model in kmeans_per_k[1:]]

3. 画图展示

plt.figure(figsize=(8,4))
plt.plot(range(2,10),silhouette_scores,'bo-')
# plt.axis([1,8.5,0,1300])
plt.show()

4. 效果展示

   轮廓系数指标应当越大越好，从此图中可以观察到簇的个数应当为4
   

8. Kmeans存在的问题

1. 生成原始数据集

X1, y1 = make_blobs(n_samples=1000, centers=((4, -4), (0, 0)), random_state=42)
X1 = X1.dot(np.array([[0.374, 0.95], [0.732, 0.598]]))
X2, y2 = make_blobs(n_samples=250, centers=1, random_state=42)
X2 = X2 + [6, -8]
X = np.r_[X1, X2]
y = np.r_[y1, y2]

plot_data(X)

2. 原始数据集的效果展示
   

3. 默认的中心点与随机生成的中心点进行对比

kmeans_good = KMeans(n_clusters = 3,init = np.array([[-1.5,2.5],[0.5,0],[4,0]]),n_init=1,random_state=42)
kmeans_bad = KMeans(n_clusters = 3,random_state=42)
kmeans_good.fit(X)
kmeans_bad.fit(X)

4. 绘制图形

plt.figure(figsize=(10,4))
plt.subplot(121)
plot_decision_boundaries(kmeans_good,X)
# plt.title('Good - inertia = {}'.fotmat(kmeans_good.inertia_))

plt.subplot(122)
plot_decision_boundaries(kmeans_bad,X)
# plt.title('Bad - inertia = {}'.fotmat(kmeans_bad.inertia_))

5. 效果展示
   

9. 图像分割实例

1. 加载图片

# ladybug.png
from matplotlib.image import imread
image = imread('ladybug.png')
image.shape

2. 重塑数据

X = image.reshape(-1,3)

3. 进行训练

# 进行训练
kmeans = KMeans(n_clusters = 8,random_state=42).fit(X)

# 八个中心位置
# kmeans.cluster_centers_

4. 把原始图像的像素数转化为特定的类别

# 通过标签找到对应的中心点，并且把数据还原成三维数据
segmented_img = kmeans.cluster_centers_[kmeans.labels_].reshape(533, 800, 3)
# 此时的图像当中只有八种不同的像素点
segmented_img

5. 把原始数据分为不同的簇，以进行对比实验

segmented_imgs = []
n_colors = (10,8,6,4,2)
for n_clusters in n_colors:
    kmeans =  KMeans(n_clusters,random_state=42).fit(X)
    segmented_img = kmeans.cluster_centers_[kmeans.labels_]
    segmented_imgs.append(segmented_img.reshape(image.shape))

6. 绘制图形

plt.figure(figsize = (10,5))
plt.subplot(231)
plt.imshow(image)
plt.title('Original image')

for idx,n_clusters in enumerate(n_colors):
    plt.subplot(232+idx)
    plt.imshow(segmented_imgs[idx])
    plt.title('{}colors'.format(n_clusters))

7. 效果展示

   从图像来看，当簇的个数为2的时候，可以很好的把图像的前景和背景分割出来
   

10. 半监督学习

1. 加载数据集并对数据集进行拆分

   首先，让我们将训练集聚类为50个集群，然后对于每个聚类，让我们找到最靠近质心的图像。 我们将这些图像称为代表性图像：

from sklearn.datasets import load_digits
# 加载并返回数字数据集（分类）
X_digits,y_digits = load_digits(return_X_y = True)

from sklearn.model_selection import train_test_split
# 将数组或矩阵切分为随机训练和测试子集
X_train,X_test,y_train,y_test = train_test_split(X_digits,y_digits,random_state=42)

2. 进行训练

• 第一类：直接选择50个样本进行逻辑回归的计算

# 使用逻辑回归进行半监督学习
from sklearn.linear_model import LogisticRegression
n_labeled = 50

log_reg = LogisticRegression(random_state=42)
log_reg.fit(X_train[:n_labeled], y_train[:n_labeled])
log_reg.score(X_test, y_test)

结果：0.8266666666666667

• 第二类：用聚类算法找到距离簇中心最近的具有代表性的点，再进行逻辑回归的计算

# 对训练数据进行聚类
k = 50
kmeans = KMeans(n_clusters=k, random_state=42)
# 得到1347个样本到每个簇的距离
X_digits_dist = kmeans.fit_transform(X_train)

# 找簇中距离质心最近的点的索引
representative_digits_idx = np.argmin(X_digits_dist,axis=0)

# 把索引回传到训练样本中,找到当前的数据
X_representative_digits = X_train[representative_digits_idx]

现在让我们绘制这些代表性图像并手动标记它们：

# 画图并展示
plt.figure(figsize=(8, 2))
for index, X_representative_digit in enumerate(X_representative_digits):
    plt.subplot(k // 10, 10, index + 1)
    plt.imshow(X_representative_digit.reshape(8, 8), cmap="binary", interpolation="bilinear")
    plt.axis('off')

plt.show()

效果展示：

根据以上结果进行手动标记标签：

# 手动打标签
y_representative_digits = np.array([
    4, 8, 0, 6, 8, 3, 7, 7, 9, 2,
    5, 5, 8, 5, 2, 1, 2, 9, 6, 1,
    1, 6, 9, 0, 8, 3, 0, 7, 4, 1,
    6, 5, 2, 4, 1, 8, 6, 3, 9, 2,
    4, 2, 9, 4, 7, 6, 2, 3, 1, 1])

现在我们有一个只有50个标记实例的数据集，它们中的每一个都是其集群的代表性图像，而不是完全随机的实例，然后去训练：

log_reg = LogisticRegression(random_state=42)
log_reg.fit(X_representative_digits, y_representative_digits)
log_reg.score(X_test, y_test)

结果：0.92

• 第三类：将标签传播到同一群集中的所有其他实例，然后进行逻辑回归的计算

# 先做一个空的标签
y_train_propagated = np.empty(len(X_train), dtype=np.int32)
# 遍历打标签
for i in range(k):
    y_train_propagated[kmeans.labels_==i] = y_representative_digits[i]
    
log_reg = LogisticRegression(random_state=42)
log_reg.fit(X_train, y_train_propagated)

log_reg.score(X_test, y_test)

结果：0.9288888888888889

• 第四类：选择前20个来进行逻辑回归的计算

## 核心：簇 -> 索引 -> 样本
percentile_closest = 20

X_cluster_dist = X_digits_dist[np.arange(len(X_train)), kmeans.labels_]
for i in range(k):
    in_cluster = (kmeans.labels_ == i)
    # 选择属于当前簇的所有样本
    cluster_dist = X_cluster_dist[in_cluster] 
    # 排序找到前20个
    cutoff_distance = np.percentile(cluster_dist, percentile_closest) 
    # False True结果
    above_cutoff = (X_cluster_dist > cutoff_distance) 
    X_cluster_dist[in_cluster & above_cutoff] = -1

# 找到索引
partially_propagated = (X_cluster_dist != -1)
# 回传到样本
X_train_partially_propagated = X_train[partially_propagated]
y_train_partially_propagated = y_train_propagated[partially_propagated]

# 进行训练
log_reg = LogisticRegression(random_state=42)
log_reg.fit(X_train_partially_propagated, y_train_partially_propagated)

log_reg.score(X_test, y_test)

结果：0.9444444444444444

11. DBSCAN算法

1. 准备数据集

from sklearn.datasets import make_moons
X, y = make_moons(n_samples=1000, noise=0.05, random_state=42)

2. 导包并进行对比实验

from sklearn.cluster import DBSCAN
# eps:半径值,min_samples：一个点被视为核心点的邻域内的样本数

# 进行对比实验
dbscan = DBSCAN(eps = 0.05,min_samples=5)
dbscan.fit(X)

dbscan2 = DBSCAN(eps = 0.2,min_samples=5)
dbscan2.fit(X)

3. 绘制图形

def plot_dbscan(dbscan, X, size, show_xlabels=True, show_ylabels=True):
    core_mask = np.zeros_like(dbscan.labels_, dtype=bool)
    core_mask[dbscan.core_sample_indices_] = True
    anomalies_mask = dbscan.labels_ == -1
    non_core_mask = ~(core_mask | anomalies_mask)

    cores = dbscan.components_
    anomalies = X[anomalies_mask]
    non_cores = X[non_core_mask]
    
    plt.scatter(cores[:, 0], cores[:, 1],
                c=dbscan.labels_[core_mask], marker='o', s=size, cmap="Paired")
    plt.scatter(cores[:, 0], cores[:, 1], marker='*', s=20, c=dbscan.labels_[core_mask])
    plt.scatter(anomalies[:, 0], anomalies[:, 1],
                c="r", marker="x", s=100)
    plt.scatter(non_cores[:, 0], non_cores[:, 1], c=dbscan.labels_[non_core_mask], marker=".")
    if show_xlabels:
        plt.xlabel("$x_1$", fontsize=14)
    else:
        plt.tick_params(labelbottom='off')
    if show_ylabels:
        plt.ylabel("$x_2$", fontsize=14, rotation=0)
    else:
        plt.tick_params(labelleft='off')
    plt.title("eps={:.2f}, min_samples={}".format(dbscan.eps, dbscan.min_samples), fontsize=14)

plt.figure(figsize=(18, 4))

plt.subplot(131)
plt.plot(X[:,0],X[:,1],'b.')
plt.xlabel("$x_1$", fontsize=14)
plt.ylabel("$x_2$", fontsize=14,rotation=0)
plt.title("Original image")

plt.subplot(132)
plot_dbscan(dbscan, X, size=100)

plt.subplot(133)
plot_dbscan(dbscan2, X, size=600, show_ylabels=True)

plt.show()

4. 效果展示

   图1为原始图像；图2为半径0.05，邻域点为5的DBSCAN聚类效果；图3为半径0.2，邻域点为5的DBSCAN聚类效果。从图中的效果来看，图3可以达到预期的效果