机器学习 —— 支持向量机SVM(Support Vector Machine)
【关键词】支持向量,最大几何间隔,拉格朗日乘子法
一、支持向量机的原理
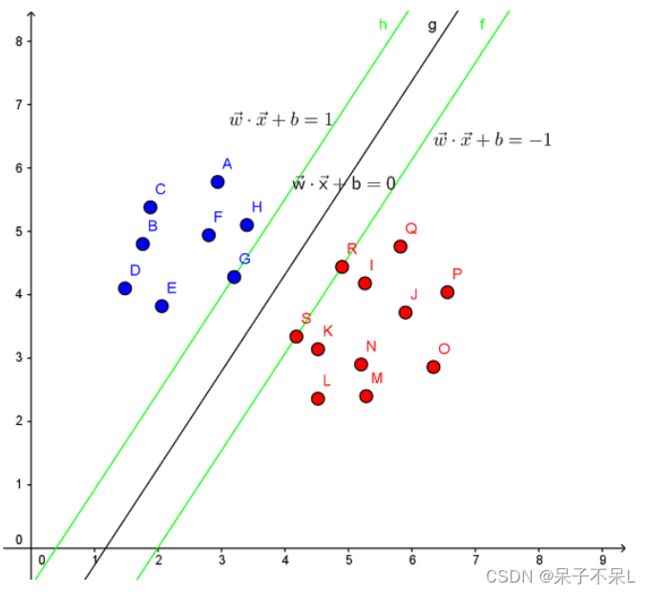
Support Vector Machine。支持向量机,其含义是通过支持向量运算的分类器。其中“机”的意思是机器,可以理解为分类器。 那么什么是支持向量呢?在求解的过程中,会发现只根据部分数据就可以确定分类器,这些数据称为支持向量。 见下图,在一个二维环境中,其中点R,S,G点和其它靠近中间黑线的点可以看作为支持向量,它们可以决定分类器,也就是黑线的具体参数。
解决的问题:
- 线性分类
在训练数据中,每个数据都有n个的属性和一个二类类别标志,我们可以认为这些数据在一个n维空间里。我们的目标是找到一个n-1维的超平面(hyperplane),这个超平面可以将数据分成两部分,每部分数据都属于同一个类别。 其实这样的超平面有很多,我们要找到一个最佳的。因此,增加一个约束条件:这个超平面到每边最近数据点的距离是最大的。也成为最大间隔超平面(maximum-margin hyperplane)。这个分类器也成为最大间隔分类器(maximum-margin classifier)。 支持向量机是一个二类分类器。
- 非线性分类
SVM的一个优势是支持非线性分类。它结合使用拉格朗日乘子法和KKT条件,以及核函数可以产生非线性分类器。
二、实战
1、画出决策边界
导包sklearn.svm
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
# SVC: 分类
# SVR:回归
from sklearn.svm import SVC,SVR随机生成数据,并且进行训练
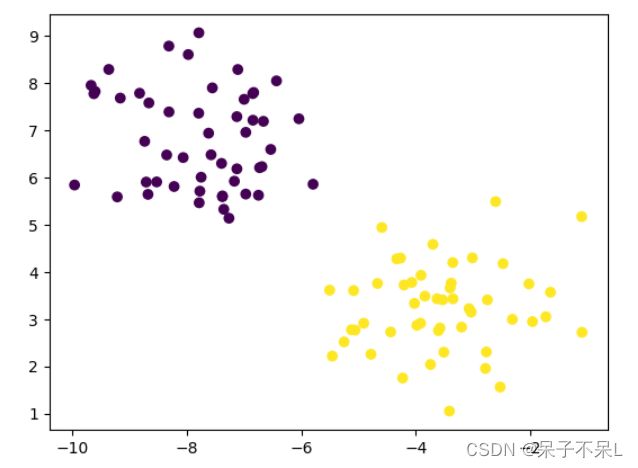
- from sklearn.datasets import make_blobs
from sklearn.datasets import make_blobs
data,target = make_blobs(centers=2)
target
plt.scatter(data[:,0],data[:,1],c=target)创建SVC模型(使用线性核函数),并训练
# C=1.0, 惩罚系数,C越大越严格(有可能过拟合),C越小越不严格
# kernel='rbf', 核函数
# linear:线性核函数,不常用
# rbf:默认值,高斯核函数,基于半径的和函数,可以解决非线性问题
# poly:多项式核函数
svc = SVC(C=1.0,kernel='linear')
svc.fit(data,target)提取系数获取斜率
w1,w2 = svc.coef_[0]
w1,w2
# (1.0522835977410239, -0.8013229035839045)线性方程的截距
b = svc.intercept_[0]
b
# 9.794733796740164得到线性方程
# w1 * x1 + w2 * x2 + b = 0
# x2 作为y轴,x1作为x轴
# x2 = -(w1 * x1 + b) / w2画图
plt.scatter(data[:,0],data[:,1],c=target)
x = np.linspace(data[:,0].min(),data[:,0].max(),20)
y = -(w1 * x + b) / w2
plt.plot(x,y)获取支持向量
svc.support_vectors_
'''
array([[-5.79772872, 5.85766345],
[-4.59471853, 4.94156096]])
'''画出支持向量所在直线
plt.scatter(data[:,0],data[:,1],c=target)
x = np.linspace(data[:,0].min(),data[:,0].max(),20)
y = -(w1 * x + b) / w2
plt.plot(x,y)
# 画支持向量
vectors = svc.support_vectors_
plt.scatter(vectors[:,0],vectors[:,1],c='r',alpha=0.3,s=200)
# 活出支持向量所在的虚线
# vectors = array([[-4.64189396, 5.45729366],
# [-6.04692482, 7.04214351],
# [-3.63094168, 5.92881411],
# [-4.74569939, 7.93088232]])
b1 = -(w1 * vectors[0,0] + w2 * vectors[0,1])
b2 = -(w1 * vectors[1,0] + w2 * vectors[1,1])
y1 = -(w1 * x + b1) / w2
y2 = -(w1 * x + b2) / w2
plt.plot(x,y1,ls='--')
plt.plot(x,y2,ls='--')2、使用多种核函数对iris数据集进行分类
导包
from sklearn.datasets import load_iris
from sklearn.datasets import load_iris
data,target = load_iris(return_X_y=True)
data.shape
# (150, 4)提取数据只提取两个特征,方便画图
data2 = data[:,:2].copy()
plt.scatter(data2[:,0],data2[:,1],c=target)def get_XY(data2):
x = np.linspace(data2[:,0].min(),data2[:,0].max(),1000)
y = np.linspace(data2[:,1].min(),data2[:,1].max(),1000)
X,Y = np.meshgrid(x,y)
XY = np.c_[X.ravel(),Y.ravel()]
return X,Y,XY
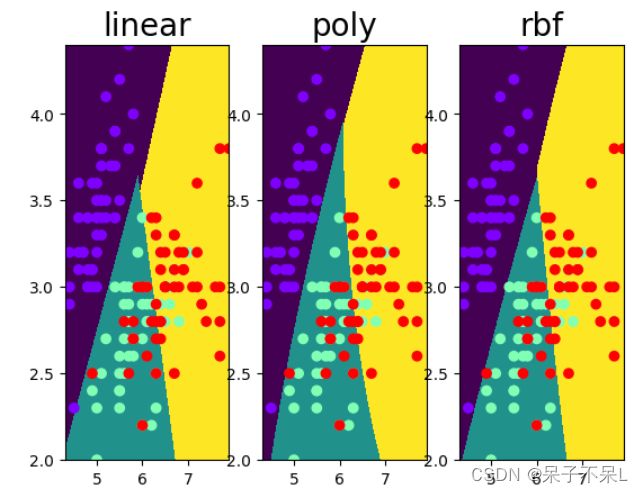
X,Y,XY = get_XY(data2)创建支持向量机的模型:'linear', 'poly'(多项式), 'rbf'(Radial Basis Function:基于半径函数)
svc_dict = {
'linear':SVC(kernel='linear'),
'poly':SVC(kernel='poly'),
'rbf':SVC(kernel='rbf')
}
for i,key in enumerate(svc_dict):
# 训练
svc = svc_dict[key]
svc.fit(data2,target)
# 预测
y_pred = svc.predict(XY)
# 画图
axes = plt.subplot(1,3,i+1)
axes.pcolormesh(X,Y,y_pred.reshape(1000,1000),shading='auto')
axes.scatter(data2[:,0],data2[:,1],c = target,cmap='rainbow')
axes.set_title(key,fontsize=20)3、SVM分离坐标点
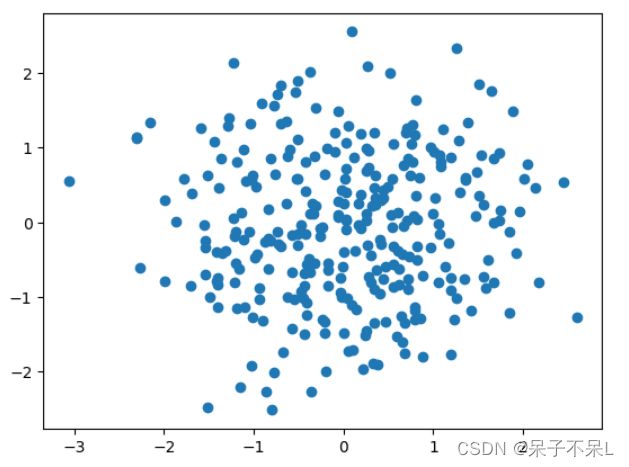
生成随机数据
data = np.random.randn(300,2)
data
plt.scatter(data[:,0],data[:,1])将1,3象限 和 2,4象限区分颜色
target = (data[:,0] * data[:,1] > 0) * 1
target
# target = 1: 一三象限;target = 0:二四象限
'''
array([1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1,
1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1,
1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0,
1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0,
0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0,
0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1,
1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0,
0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1,
0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0,
1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0,
0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0,
0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1,
1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1])
'''
plt.scatter(data[:,0],data[:,1],c=target)
使用基于半径核函数
svc = SVC()
svc.fit(data,target)
创造一个范围的点以及meshgrid
def get_XY(data):
x = np.linspace(data[:,0].min(),data[:,0].max(),1000)
y = np.linspace(data[:,1].min(),data[:,1].max(),1000)
X,Y = np.meshgrid(x,y)
XY = np.c_[X.ravel(),Y.ravel()]
return X,Y,XY
X,Y,XY = get_XY(data)测试点到分离超平面的距离(decision_function)
distance = svc.decision_function(XY)
distance
'''
array([0.2733806 , 0.27487237, 0.27637551, ..., 0.33516833, 0.33292289,
0.33069489])
'''把距离当成一个二维的图片
画出图形
- 等高线
- C = plt.contour(X, Y, distance.reshape(1000, 1000))
plt.figure(figsize=(5,5),dpi=150)
plt.imshow(distance.reshape(1000,1000),extent=[data[:,0].min(),data[:,0].max(),data[:,1].min(),data[:,1].max()])
# 等高线
C = plt.contour(X,Y,distance.reshape(1000,1000))
plt.clabel(C) # 显示等高线
plt.scatter(data[:,0],data[:,1],c=target)4、使用SVM多种核函数进行回归
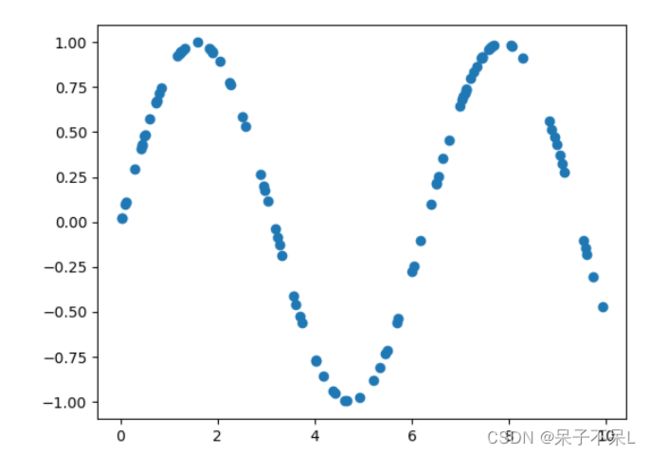
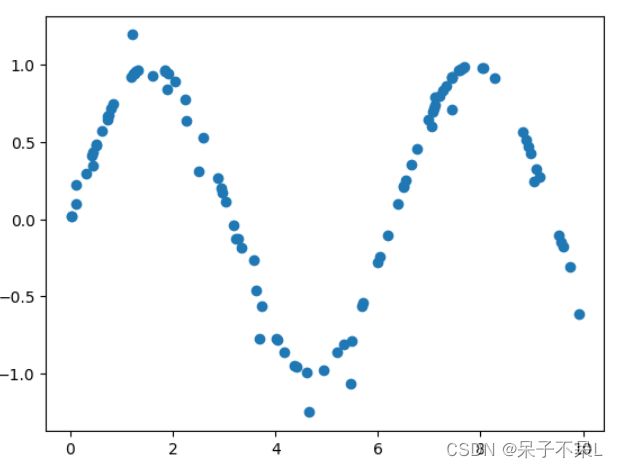
自定义样本点rand,并且生成sin值
x = np.random.random(100) * 10
y = np.sin(x)
plt.scatter(x, y)数据加噪
y[ : : 5] += np.random.randn(20) * 0.2
plt.scatter(x, y)提供测试数据
x_test = np.linspace(0, 10, 100).reshape(-1, 1)用不同的核函数预测
# linear
linear = SVR(kernel='linear')
linear.fit(x.reshape(-1, 1), y)
y_linear = linear.predict(x_test)
# poly
poly = SVR(kernel='poly')
poly.fit(x.reshape(-1, 1), y)
y_poly = poly.predict(x_test)
# rbf
rbf = SVR(kernel='rbf')
rbf.fit(x.reshape(-1, 1), y)
y_rbf = rbf.predict(x_test)
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
# knn
knn = KNeighborsRegressor(n_neighbors=5)
knn.fit(x.reshape(-1, 1), y)
y_knn = knn.predict(x_test)
# tree
tree = DecisionTreeRegressor()
tree.fit(x.reshape(-1, 1), y)
y_ = tree.predict(x_test)绘制图形,观察三种支持向量机内核不同
plt.scatter(x, y)
plt.plot(x_test, y_linear, label='Linear')
plt.plot(x_test, y_poly, label='poly')
plt.plot(x_test, y_rbf, label='rbf')
plt.plot(x_test, y_knn, label='knn')
plt.plot(x_test, y_, label='tree')
plt.legend()