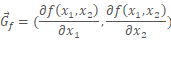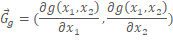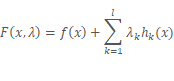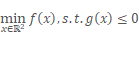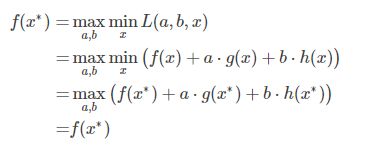拉格朗日乘子法详解
一、拉格朗日乘子法简介
拉格朗日乘子法的应用十分广泛，它是SVM的理论基础，是凸优化的重要研究部分。它用于求解约束条件下的极值问题，过程简单巧妙，也是各类考试的常考题型。然而，拉格朗日乘子法的原理我却一直模模糊糊，每次看的时候才知道，一段时间不看就又忘了，所以特地写这篇博客来供自己时刻学习。
先从一个简单的例子开始：
假如我们需要求一个函数
的最小值，即
，约束条件为
。我们用拉格朗日乘子法来求解：
首先用
描述约束条件，即
。
而后引入拉格朗日乘子λ，并构造一个新的函数：
因为
，于是
，因此当
取得极小值时有：
(1)
于是得到：
=>
。
即当
=
=1时，
取得最小值，最小值为2。这就是拉格朗日乘子法求解过程。
拉格朗日乘子法非常巧妙，但其中的原理却难以琢磨，从几何角度观察，我们可以更加直观地理解拉格朗日乘子法的原理以及这个乘子λ的几何含义。
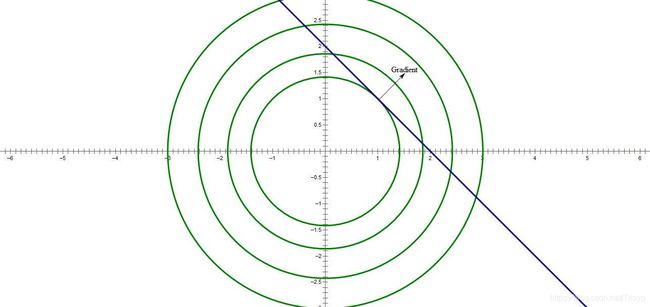
首先我们观察约束条件
，在
平面上是一条直线如下图中的蓝色直线所示。
再看
，令
这表示
的某一条等高线，随着r的改变我们得到了多条等高线，在上图中以绿色圆圈表示。
在图中，如果某一条等高线
与直线
相交，则表示在
的约束条件下，
可以取到r的值。为了求得
的最小值，在保证绿色圆圈与蓝色直线有交点的前提下，逐渐将r缩小，直到绿色等高线圆小到与蓝色直线相切，此时r0最小，我们认为获得了最小值
。
下面我们来计算
，在图中我们看到等高线圆
与约束直线相切。此时在切点处，等高线圆与约束直线具有相同的切线方向与法线方向。
又因为等高线f
的切线方向与
在该点的梯度方向相互正交，于是
的法线方向即是
的梯度方向，而该梯度方向为
同理直线
的法线方向也就是的梯度方向
在切点处Gf与Gg的方向相同，即相切。那么f ( x ) 和 g ( x ) 在这一点的梯度一定是成比例的（具体理解起来就是法向量一定成比例）。
因此我们引入乘子λ，并且有
=>
（2）
上式与式(1)相同。这个方程组总共包含n + 1个方程（梯度是一个向量，梯度等于0必须每一维都为0），恰好可以解出所有的λ 和 
。
到此我们也已经获得了与拉格朗日乘子法相一致的结论。于是我们从几何角度解释了拉格朗日乘子引入的过程，也验证了拉格朗日乘子法的结论。
二、拉格朗日乘子法求解带等式约束的最优化问题
拉格朗日求得的并不一定是最优解，只有在凸优化的情况下，才能保证得到的是最优解，所以我们说拉格朗日乘子法得到的为可行解，其实就是局部极小值。
1、构造拉格朗日函数
之所以这样构造的原理我们可以继续看上面式（2）,我们把式子的右边移到左边，并把常数移进微分算子，得到：
把这个式子重新解释一下，这个就是函数
无约束条件下极值点的充分条件。
2、构造完之后就可以分别对参数求偏导，并令其等于0，就能解出无约束极值和极值所对应的点。
三、引入KKT条件求带不等式约束条件的最优化问题
所谓的KKT条件，是指对一类符合条件的所有拉格朗日乘子法问题进行公式化求解的过程。在机器学习中，我们解决的问题一般最后都化为目标函数最优化问题，即转化为在给定约束条件下最大或最小化目标函数。
约束条件会有一般包括以下三类：
1）仅含等式约束
2）仅含不等式约束
3）等式和不等式约束混合型
当然还有一类没有任何约束条件的最优化问题。仅含等式约束的目标函数不再赘述。
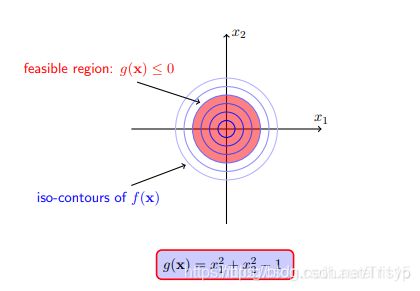
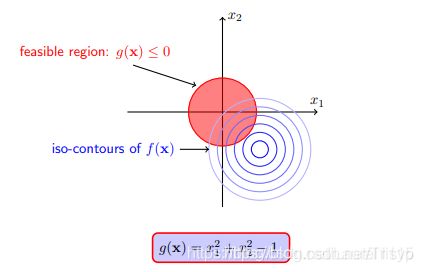
对于不等式约束g(x)<=0，和等式约束h(x)=0不一样，h(x)=0可以在平面上画出一条等高线，而g(x)<=0是一个区域，很多个等高线堆叠而成的一块区域，我们把这块区域称为可行域。
不等式约束分两种情况来讨论，第一种是原有函数的（不考虑可行域限制时的）极值点落在可行域内（不包含边界），第二种是原有函数的（不考虑可行域限制时的）极值点落在可行域外（包含边界）。
下面举两个例子来解释这两种情况，然后总结两种情况给出转换求解。
（一）带不等式约束条件的最优化
在有不等式g(x)<=0的约束下，可行解 x 只能在 g(x)<0 或者 g(x)=0 的区域里取得：
当可行解 x 落在 g(x)<0 的区域内，此时直接极小化 f(x) 即可；
当可行解 x 落在 g(x)=0 即边界上，此时等价于等式约束优化问题.
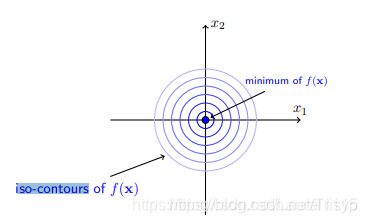
case1：当约束区域包含目标函数原有的的可行解时，此时加上约束可行解仍落在约束区域内部，对应 g(x)<0 的情况，这时约束条件不起作用；
现在我们假设问题是：
，其中
。
我们很容易知道f(x)的最小值在（0，0），等高线如下图：
接下来我们画上g(x1,x2)限制的可行域（以（0，0）为圆心，半径为1的圆型区域，包括边界）：
很明显这个约束并不起作用，函数f(x1,x2)的极值点不变，这种情况约束不起作用，考虑极小值点x*，这个时候，g(x*) < 0，f(x*)的梯度等于0。
case2：当约束区域不包含目标函数原有的可行解时，此时加上约束后可行解落在边界 g(x)=0 上。下面我们考虑另外一个不等式约束下的问题：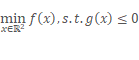
，其中
我们可以看一下这个问题的等高线情况：
以上两种情况就是说，要么可行解落在约束边界上即得 g(x)=0，要么可行解落在约束区域内部，此时约束不起作用，令 λ=0 消去约束即可，所以无论哪种情况都会得到λ
（也就是KKT条件的其中之一）。
还有一个问题是 λ 的取值，在等式约束优化中，约束函数与目标函数的梯度只要满足平行即可，而在不等式约束中则不然，若 λ≠0，这便说明 可行解 x 是落在约束区域的边界上的，这时可行解应尽量靠近无约束时的解，所以在约束边界上，目标函数的负梯度方向应该远离约束区域朝向无约束时的解，此时正好可得约束函数的梯度方向与目标函数的负梯度方向应相同：
上式需要满足的要求是拉格朗日乘子 λ>0
（二）满足KKT条件
可见对于不等式约束，只要满足一定的条件，依然可以使用拉格朗日乘子法解决，这里的条件便是 KKT 条件。
对于如下：
我们定义的拉格朗日函数：
这时，KKT条件如下：
满足 KKT 条件后极小化 Lagrangian 即可得到在不等式约束条件下的可行解。 KKT 条件看起来很多，其实很好理解:
1) 拉格朗日取得可行解的必要条件；
2) 这就是以上分析的一个比较有意思的约束，称作松弛互补条件；
3∼4) 初始的约束条件；
5) 不等式约束的 Lagrange Multiplier 需满足的条件
（三）原最优化问题转对偶问题
每个线性规划问题都有一个与之对应的对偶问题，对偶问题有非常良好的性质，以下列举几个：
1）对偶问题的对偶是原问题；
2）无论原始问题是否是凸的，对偶问题都是凸优化问题；
3）对偶问题可以给出原始问题一个下界；
4）当满足一定条件时，原始问题与对偶问题的解是完全等价的；
任何满足强对偶性的优化问题，只要其目标函数与约束函数可微，任一对原始问题与对偶问题的解都是满足 KKT 条件的。即满足强对偶性的优化问题中，若x*为原始问题的最优解，α* ,β* 为对偶问题的最优解，则可得 x*,α*,β* 满足 KKT 条件。
当原始问题是凸优化问题,且存在x*,α*,β*满足 KKT 条件，那么它们分别是原始问题和对偶问题的极值点并且强对偶性成立。
当满足KKT条件时， f(x)与
是等价的。
因此我们的目标函数可以写为: 
如果用对偶表达式: 
，由于我们的优化是满足强对偶的（满足KKT条件），强对偶就是说对偶式子的最优值是等于原问题的最优值的，所以在取得最优值 x∗ 的条件下，它满足：
我们来看看中间两个式子发生了什么事情：
可以看到上式本质上是说
在 x∗ 取得了最小值,对于函数 f(x)+a⋅g(x)+b⋅h(x)，求取导数要等于零，即
这就是KKT条件中第一个条件: 
所有上述说明，满足强对偶条件的优化问题的最优值都必须满足KKT条件,也就是说当满足KKT条件时原始问题与其对偶问题具有相同的最优解。
参考网址：
https://www.cnblogs.com/jason-wyf/p/6727524.html
https://blog.csdn.net/Laurel1115/article/details/88238944
https://blog.csdn.net/weixin_44273380/article/details/109016774