【菜菜的sklearn课堂笔记】数据预处理和特征工程-数据预处理-数据无量纲化 & 缺失值

视频作者：菜菜TsaiTsai
链接：【技术干货】菜菜的机器学习sklearn【全85集】Python进阶_哔哩哔哩_bilibili

数据挖掘的五大流程：

1. 获取数据
2. 数据预处理
   数据预处理是从数据中检测，纠正或删除损坏，不准确或不适用于模型的记录的过程
   可能面对的问题有：数据类型不同，比如有的是文字，有的是数字，有的含时间序列，有的连续，有的间断。也可能，数据的质量不行，有噪声，有异常，有缺失，数据出错，量纲不一，有重复，数据是偏态，数据量太大或太小
   数据预处理的目的：让数据适应模型，匹配模型的需求
3. 特征工程：
   特征工程是将原始数据转换为更能代表预测模型的潜在问题的特征的过程，可以通过挑选最相关的特征，提取特征以及创造特征来实现。其中创造特征又经常以降维算法的方式实现。
   可能面对的问题有：特征之间有相关性，特征和标签无关，特征太多或太小，或者干脆就无法表现出应有的数据现象或无法展示数据的真实面貌
   特征工程的目的：降低计算成本，提升模型上限
4. 建模，测试模型并预测出结果
5. 上线，验证模型效果

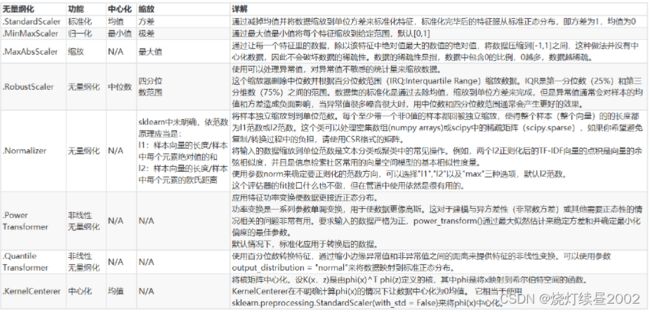
数据无量纲化

在机器学习算法实践中，我们往往有着将不同规格的数据转换到同一规格，或不同分布的数据转换到某个特定分布的需求，这种需求统称为将数据“无量纲化”。

数据的无量纲化可以是线性的，也可以是非线性的。线性的无量纲化包括中心化（Zero-centered或者Mean-subtraction）处理和缩放处理（Scale）。中心化的本质是让所有记录减去一个固定值，即让数据样本数据平移到某个位置。缩放的本质是通过除以一个固定值，将数据固定在某个范围之中，取对数也算是一种缩放处理。

可以认为归一化和标准化都是无量纲化的方法

数据的无量纲化是对于特征来说的，因此fit接口只能导入至少二维数组

归一化

当数据(x)按照最小值中心化后，再按极差（最大值 - 最小值）缩放，数据移动了最小值个单位，并且会被收敛到$[0,1]$之间，而这个过程，就叫做数据归一化(Normalization，又称Min-Max Scaling)，即
$$x^{\ast }=\frac{x-\min (x)}{\max (x)-\min (x)}$$

实际上收敛区间我们可以自己指定

Normalization是归一化，不是正则化，真正的正则化是regularization，不是数据预处理的一种手段。

sklearn中对应归一化的方法为MinMaxScaler

MinMaxScaler(feature_range=(0, 1), copy=True)
# feature_range也就是上面说的收敛到指定的区间

from sklearn.preprocessing import MinMaxScaler
import pandas as pd

data = [[-1,2],[-0.5,6],[0,10],[1,18]]
scaler = MinMaxScaler()# 实例化
scaler = scaler.fit(data) # 这里本质是生成min(x)和max(x)
result = scaler.transform(data) # 通过接口导出结果
result
---
array([[0.  , 0.  ],
       [0.25, 0.25],
       [0.5 , 0.5 ],
       [1.  , 1.  ]])

# 可以用fit_transform(data)一步完成
result = MinMaxScaler().fit_transform(data)

scaler.inverse_transform(result) # 将归一化后的结果逆转，即从结果找回输入数据
---
array([[-1. ,  2. ],
       [-0.5,  6. ],
       [ 0. , 10. ],
       [ 1. , 18. ]])

# 使用MinMaxScaler的参数feature_range实现将数据归一化到指定的范围
data = [[-1,2],[-0.5,6],[0,10],[1,18]]
scaler = MinMaxScaler(feature_range=[5,10])
result = scaler.fit_transform(data)
result
---
array([[ 5.  ,  5.  ],
       [ 6.25,  6.25],
       [ 7.5 ,  7.5 ],
       [10.  , 10.  ]])

当X中的特征数量非常多的时候，fit会报错并表示，数据量太大了，计算不了。此时使用partial_fit作为训练接口

scaler = scaler.partial_fit(data)

使用numpy实现归一化

import numpy as np
X = np.array([[-1,2],[-0.5,6],[0,10],[1,18]])

X_nor = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
# axis=0跨列计算，axis=1跨行计算
X_nor
---
array([[0.  , 0.  ],
       [0.25, 0.25],
       [0.5 , 0.5 ],
       [1.  , 1.  ]])

# 逆转归一化
X_returned = X_nor * (X.max(axis=0) - X.min(axis=0)) + X.min(axis=0)
X_returned
---
array([[-1. ,  2. ],
       [-0.5,  6. ],
       [ 0. , 10. ],
       [ 1. , 18. ]])

标准化

当数据X按均值$\mu$中心化后，再按标准差$\sigma$缩放，如果原数据服从正态分布，那么新数据就会服从为均值为0，方差为1的正态分布（即标准正态分布），而这个过程，就叫做数据标准化(Standardization，又称Z-score normalization)，即
$$x^{\ast }=\frac{x-\mu }{\sigma }$$

在sklearn中对应方法为StandardScaler

StandardScaler(copy=True, with_mean=True, with_std=True)
# 参数一般不动，默认就行

from sklearn.preprocessing import StandardScaler
data = [[-1,2],[-0.5,6],[0,10],[1,18]]

scaler = StandardScaler()
scaler = scaler.fit(data)# 本质是生成均值和方差

scaler.mean_ # 结果是一个数组
---
array([-0.125,  9.   ])

scaler.var_
---
array([ 0.546875, 35.      ])

X_std = scaler.transform(data) # 通过接口导出结果
X_std # 两个数据大小不同，但分布一致
---
array([[-1.18321596, -1.18321596],
       [-0.50709255, -0.50709255],
       [ 0.16903085,  0.16903085],
       [ 1.52127766,  1.52127766]])

StandardScaler().fit_transform(data)# 一步达到结果

scaler.inverse_transform(X_std) # 逆转标准化
---
array([[-1. ,  2. ],
       [-0.5,  6. ],
       [ 0. , 10. ],
       [ 1. , 18. ]])

对于StandardScaler和MinMaxScaler来说，空值NaN会被当做是缺失值，在fit的时候忽略，在transform的时候保持缺失NaN的状态显示。

更多无量纲化方法

缺失值

其实在随机森林章节里，我们提到过一些

SimpleImputer(
    ['missing_values=nan', "strategy='mean'", 'fill_value=None', 'verbose=0', 'copy=True'],
)
# missing_values:告诉缺失值是什么样的，可以是np.nan、0、-1，需要自己指定
# strategy:用什么来填补缺失值，均值mean（默认）、中值median（仅可用于数值型特征）、众数most_frequent、常量constant（可用于数值型和字符串特征）
# fill_value:如果strategy为constant，该参数取值说明常量是什么，例如ill_value=0，表示用0值填补缺失值

import pandas as pd
data = pd.read_csv(r'D:\ObsidianWorkSpace\SklearnData\Narrativedata.csv'
                  ,index_col=0
                  )
# index_col:说明某一列是行索引
data.head()
---
Age	Sex	Embarked	Survived
0	22.0	male	S	No
1	38.0	female	C	Yes
2	26.0	female	S	Yes
3	35.0	female	S	Yes
4	35.0	male	S	No

data.info() # 探索数据
---
<class 'pandas.core.frame.DataFrame'>
Int64Index: 891 entries, 0 to 890
Data columns (total 4 columns):
Age         714 non-null float64
Sex         891 non-null object
Embarked    889 non-null object
Survived    891 non-null object
dtypes: float64(1), object(3)
memory usage: 34.8+ KB

from sklearn.impute import SimpleImputer
Age = data.loc[:,'Age'].values.reshape(-1,1)# sklearn当中特征矩阵必须是二维的
imp_mean = SimpleImputer()# 实例化，默认用均值填补
imp_median = SimpleImputer(strategy='median')# 用中位数填补
imp_0 = SimpleImputer(strategy='constant',fill_value=0)# 用0填补

imp_mean = imp_mean.fit_transform(Age)
imp_median = imp_median.fit_transform(Age)
imp_0 = imp_0.fit_transform(Age)

pd.DataFrame([imp_mean.ravel(),imp_median.ravel(),imp_0.ravel()]).T.head(10)
---
	0	1	2
0	22.000000	22.0	22.0
1	38.000000	38.0	38.0
2	26.000000	26.0	26.0
3	35.000000	35.0	35.0
4	35.000000	35.0	35.0
5	29.699118	28.0	0.0
6	54.000000	54.0	54.0
7	2.000000	2.0	2.0
8	27.000000	27.0	27.0
9	14.000000	14.0	14.0

# 这里我们使用中位数填补Age
# 一般来说我们用均值填补年龄，这里由于中位数和均值差不多，因此考虑用中位数也可以
data.loc[:,'Age'] = imp_median

# 使用众数填补Embarked。实际上一般删掉，因为缺的太少了，不影响总体数据信息
# 为了后面演示，这里选择删掉
data.dropna(axis=0,inplace=True)
# 删除所有缺失值的行/列
# axis：为0删除行，为1删除列
# inplace：默认为False，生成一个复制对象，不修改原数据，设置为True，表示在原数据集上进行修改
data.info()
---
<class 'pandas.core.frame.DataFrame'>
Int64Index: 889 entries, 0 to 890
Data columns (total 4 columns):
Age         889 non-null float64
Sex         889 non-null object
Embarked    889 non-null object
Survived    889 non-null object
dtypes: float64(1), object(3)
memory usage: 34.7+ KB

用pandas填补

data_ = pd.read_csv(r'D:\ObsidianWorkSpace\SklearnData\Narrativedata.csv',index_col=0)
data_.loc[:,'Age'] = data_.loc[:,'Age'].fillna(data_.loc[:,'Age'].median())
# fillna:在DataFrame里面直接填补
data_.dropna(axis=0,inplace=True)

决策树和朴素贝叶斯可以用文字数据，因为只是算概率