梯度下降法 --- 吴恩达深度学习笔记
损失函数是衡量单一训练样例的效果。
代价函数用于衡量参数w和b的效果,在全部训练集上来衡量。
如何使用梯度下降法来训练或者学习训练集上的参数w和b?
回顾逻辑回归算法
损失函数
y ^ = σ ( w T x + b ) , σ ( z ) = 1 1 + e − z , z = w T x + b \widehat{y} = σ(w^{T}x + b),\sigma(z) = \frac 1 {1+e^{-z}},z = w^{T}x + b y =σ(wTx+b),σ(z)=1+e−z1,z=wTx+b
L ( y ^ , y ) = − ( y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ) L(\widehat{y},y) = -(ylog\widehat{y} + (1-y)log(1-\widehat{y})) L(y ,y)=−(ylogy +(1−y)log(1−y ))
损失函数可以衡量你的算法的效果,每一个训练样例都输出 y ^ ( i ) \widehat{y}^{(i)} y (i),把它与实标 y ( i ) y^{(i)} y(i)进行比较,等号右边展开完整的公式。
代价函数
J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) = − 1 m ∑ i = 1 m ( y ( i ) l o g y ^ ( i ) + ( 1 − y ( i ) ) l o g ( 1 − y ^ ( i ) ) ) J(w,b) = \frac 1 m \displaystyle\sum_{i=1}^mL(\widehat{y}^{(i)},y^{(i)}) = -\frac 1 m \displaystyle\sum_{i=1}^m (y^{(i)}log\widehat{y}^{(i)} + (1-y^{(i)})log(1-\widehat{y}^{(i)})) J(w,b)=m1i=1∑mL(y (i),y(i))=−m1i=1∑m(y(i)logy (i)+(1−y(i))log(1−y (i)))
成本函数J是参数w和b的参数,它倍定义为平均值,即1/m的损失函数之和。
承办函数衡量了参数w和b在训练集上的效果,要学习得到合适的参数w和b,很自然地,我们就想到找使得成本函数J(w,b)尽可能小的w和b。
梯度下降法

这个图中的横轴表示空间参数w和b,在实践中,w可以是更高维的,但为了方便绘图,我们让w是一个实数,b也是一个实数,成本函数J(w,b)是水平轴w和b上的曲面,曲面的高度表示了J(w,b)在某一点上的值,我们所想要做的就是,找到这样的w和b,使其对应的成本函数J值,是最小值。可以看到,成本函数J是一个凸函数,像这样的一个大碗,

因此这个凸函数看起来和这样的函数不一样,这种函数不是凸函数,因为它有很多不同的局部最优。
因此我们的成本函数J(w,b)之所以是凸函数,凸函数这性质是我们使用逻辑回归的这个特定成本函数J的重要原因。
Tips:凸函数判定方法可利用定义法、已知结论法以及函数的二阶导数,对于实数集上的凸函数,一般的判别方法是求它的二阶导数,如果其二阶导数在区间上小于等于零,就称为凸函数。如果其二阶导数在区间上恒小于0,就称为严格凸函数。
为了找到更好的参数值,我们要做的就是用某初始值,初始化w和b。对于逻辑回归而言,几乎任意的初始化方法都有效,通常用0来初始化,但是对于逻辑回归,我们通常不这么做。因为函数是凸的,无论在哪里初始化,都能达到同一点,或大致相同的点。
梯度下降法所做的就是从初始点开始,朝着最陡的下坡方向走一步,在梯度下降一步后,或许在哪里停下,因为它正试图沿着最快下降的方向,向下走。或者说,尽可能快地往下走。这是梯度下降的一次迭代。两次迭代或许会到达哪里,或者三次…等等。隐藏在图上的曲线,很有希望收敛到这个全局最优解,或者接近全局最优解。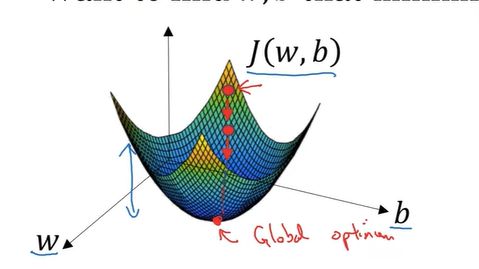
这张图阐述了梯度下降法。
示例1:J(w)和w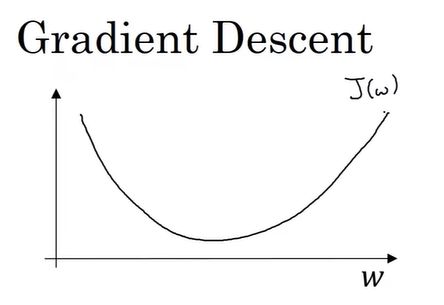
``
梯度下降法是这样做的,我们将重复执行以下的更新操作
Repeat:{
w : = w − α d J ( w ) d w w := w - α \frac {dJ(w)}{dw} w:=w−αdwdJ(w)
}
在算法收敛之前,我会重复这样去做。
在这个公式中,α表示学习率,学习率可以控制每一次迭代或者梯度下降法中的步长。
d J ( w ) d w \frac {dJ(w)}{dw} dwdJ(w)表示这个数是导数,是表示对参数w的更新或者变化量。
当我们开始编写代码,来实现梯度下降,我们会使用代码中,变量名的约定,dw表示导数,像这样编写代码
即w:=w - αdw,我们使用dw作为导数的变量名。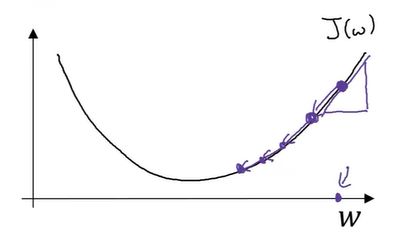
现在我们确保,梯度下降法更新是有用的,w在这对应的成本函数J(w)在曲线上的一点。
记住导数的定义,是函数在这个点的斜率,而函数的斜率是高除以宽。在这个点相切于J(w)的一个小三角形。
在这里导数是正的,新的w值等于w自身减去学习率乘导数。导数是正的,从w中减去这个乘积,接着向左走一步,像这样的梯度算法,让你的算法,逐渐地减少这个参数w。
对于另一个例子,如果w的起点在左边,这个点处的斜率将会使负的,用梯度下降法去更新,w将会减去α乘上一个负数,慢慢地,使得参数w增加,不断地用梯度下降法来迭代,w会变得越来越大。无论你初始化的位置,在左边还是在右边,梯度下降法会朝着全局最小值方向移动。
当前J(w)的梯度下降法,只有参数w,在逻辑回归中,成本函数J(w,b),是含有w和b的函数。在这种情况下,梯度下降的内循环,你必须一直重复计 w : = w − α ∂ J ( w , b ) ∂ w w:=w - α \frac {\partial J(w,b)} {\partial w} w:=w−α∂w∂J(w,b)来更新w,通过 b : = b − α ∂ J ( w , b ) ∂ b b:=b - α \frac {\partial J(w,b)} {\partial b} b:=b−α∂b∂J(w,b)来更新b。
这两个等式是实际更新参数时,进行的操作。
在微积分的符号约定中, ∂ J ( w , b ) ∂ w \frac {\partial J(w,b)} {\partial w} ∂w∂J(w,b)就是函数在w方向的斜率。
Tips:导数与偏导数的区别,导数使用的符号是小写的d,偏导数使用的符号 ∂ \partial ∂, 如果函数只有一个变量,就用小写字母d;如果函数的变量超过两个,就使用偏导数符号。
如果你看到了偏导数符号,其含义就是计算函数关于其中一个变量在对应点,所对应的斜率。
在编写代码时,一般用dw来表示 ∂ J ( w , b ) ∂ w \frac {\partial J(w,b)} {\partial w} ∂w∂J(w,b),一般用db表示 ∂ J ( w , b ) ∂ b \frac {\partial J(w,b)} {\partial b} ∂b∂J(w,b)。