K-Means聚类 和 高斯混合模型(GMM)

一、K-Means聚类算法

1.1 原理 / 步骤：

1. 我们随机初始化K个起始质心。每个数据点都分配给它最近的质心。

2. 重心被重新计算为分配给各个群集的数据点的平均值。

3. 重复步骤1和2，直到触发停止标准。

现在您可能想知道我们正在优化什么，通常是相似性度量方法：更精确的欧几里德距离或平方欧几里德距离。数据点被分配给最接近它们的簇，或者换句话说，该簇使该平方距离最小。

1.2 最佳的K值：

使用K均值时，我们需要做的一件事情就是确保选择最佳的聚类数。太少，我们可能会将具有明显差异的数据分组在一起。太多，我们将过度拟合数据，而我们的结果将不能很好地推广。

为了回答这个问题，我们将使用弯头方法（Elbow Method），这是用于此任务的常用技术。它涉及使用各种数量的K值聚类估计模型并计算聚类内平方和的负值对于使用sklearn的评分方法选择的每个簇数。请注意，这只是上述目标函数的负数。我们选择的数字是，添加更多聚类只会稍微增加分数。绘制图形时，结果看起来像肘（在这种情况下为上下肘）。簇数的最佳选择是肘部形成的位置。

其实就是我们看到的n_clusters这个超参数的最佳取舍：拐点

1.3 无法解决的问题：

1.4 应用数据集特点：

1. 数据中每个变量的方差基本上要一样

2.   每一个cluster中每个变量都是近似正态分布（或者众数等于中位数的对称分布）

3.   每一个cluster中的元素个数要几乎一样

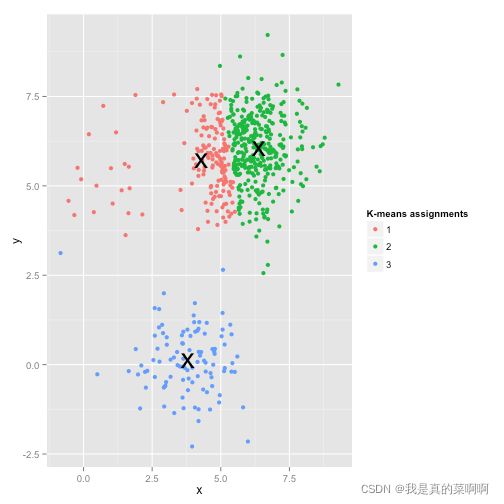
条件1和2就几乎保证了每个cluster看起来像是球形（而不是椭球形），而且是凸的。为什么条件3也很重要呢，可以看下面这个例子，尽管我们肉眼能看出三个稀疏程度不同的球状簇，但是K means却分成了三个样本数量相似的三个簇

 要求数据集是凸数据集，就是数据集内任意两点的连线上所有的点都在数据集内，否则分类效果就很差，这时候DBSCAN就比较合适了：

当然还有另一种技术可以用来解决这些问题。我们可以使用称为高斯混合模型或GMM的算法。这样做的好处是我们得到了软分配，即每个数据点都以一定的概率属于每个群集。不仅如此，GMM还对集群的方差做出了较少限制的假设。缺点是它是一个更复杂的算法。

二、GMM

2.1 思想：

        高斯混合模型（Gaussian Mixed Model，GMM）是一种常见的聚类算法，与K均值算法类似，同样使用了EM算法进行迭代计算。高斯混合模型假设每个簇的数据都是符合高斯分布（又叫正态分布）的，当前数据呈现的分布就是各个簇的高斯分布叠加在一起的结果。

        假设已知我们的数据具有两种数据分布，第一张图是只用2个高斯分布来拟合图中的数据。可以看出，我们只用2个高斯分布来拟和是不太合理的，需要推广到多个高斯分布的叠加来对数据进行拟合。第二张图是用10个高斯分布的叠加来拟合得到的结果。这就引出了高斯混合模型，即用多个高斯分布函数的线形组合来对数据分布进行拟合。理论上，高斯混合模型可以拟合出任意类型的分布。

2.2 数学表达式：

         通常我们并不能直接得到高斯混合模型的参数，而是观察到了一系列数据点，给出一个类别的数量K后，希望求得最佳的K个高斯分模型。因此，高斯混合模型的计算，便成了最佳的均值μ，方差Σ、权重 π 的寻找过程，这类问题通常通过 最大似然估计来求解。遗憾的是，此问题中直接使用最大似然估计，得到的是一 个复杂的非凸函数，目标函数是和的对数，难以展开和对其求偏导。

        在这种情况下，可以用EM算法。 EM算法是在最大化目标函数时，先固定一个变量使整体函数变为凸优化函数，求导得到最值，然后利用最优参数更新被固定的变量，进入下一个循环。具体到高 斯混合模型的求解，EM算法的迭代过程如下。

首先，初始随机选择各参数的值。然后，重复下述两步，直到收敛：

E步骤。根据当前的参数，计算每个点由某个分模型生成的概率。
M步骤。使用E步骤估计出的概率，来改进每个分模型的均值，方差和权重。

        高斯混合模型是一个生成式模型。可以这样理解数据的生成过程，假设一个最简单的情况，即只有两个一维标准高斯分布的分模型N(0,1)和N(5,1)，其权重分别为0.7和0.3。那么，在生成第一个数据点时，先按照权重的比例，随机选择一个分布，比如选择第一个高斯分布，接着从N(0,1)中生成一个点，如−0.5，便是第一个数据点。在生成第二个数据点时，随机选择到第二个高斯分布N(5,1)，生成了第二个点4.7。如此循环执行，便生成出了所有的数据点。

        也就是说，我们并不知道最佳的K个高斯分布的各自3个参数，也不知道每个 数据点究竟是哪个高斯分布生成的。所以每次循环时，先固定当前的高斯分布不变，获得每个数据点由各个高斯分布生成的概率。然后固定该生成概率不变，根据数据点和生成概率，获得一个组更佳的高斯分布。循环往复，直到参数的不再变化，或者变化非常小时，便得到了比较合理的一组高斯分布。

这意味着每个数据点可能已经由任何分布以相应的概率生成。实际上，每个分布都有一定的“责任”来生成特定的数据点。

我们如何估计这种类型的模型？好吧，我们可以做的一件事就是为每个数据点引入一个潜在变量 （gamma）。这假定是通过使用关于潜在变量的一些信息生成的每个数据点γ。换句话说，它告诉我们哪个高斯生成了特定的数据点。但是实际上，我们没有观察到这些潜在变量，因此我们需要对其进行估计。我们如何做到这一点？好吧，对我们来说幸运的是，在这样的情况下已经有了一种算法，期望最大化（EM）算法。

开始之前先稍微复习EM会用到的线性代数或是最优化理论的内容：

参考资料：

机器学习无监督算法|高斯混合模型(GMM)的来龙去脉，看不懂来找我！当场推导