FPN论文笔记

FPN论文笔记

现在看FPN和Inception并行结构融合有点像，FPN上采样同时横向连接相加，Inception是堆叠几个感受野不同的feature，融合的思想有点相似。

FPN是什么？

Feature Pyramid Networks,用于特征抽取（feature extractor）

第一个是featureized image pyramid，每层都会预测并输出，很慢。

第二个文章中经常提到，single-scale的，传统都是这种多层卷积获得feature map后输出。

第三个在single-scale的feature map的基础上建立的。

第四个是特征金字塔网络(FPN)，自下到上，自上到下以及横向连接的网络。

之前都不用金字塔结构是因为其访存密集并且计算密集。

如图，FPN融合时像一个挂载的模块，例如挂在resnet上，再通过这个模块进行操作。FPN每层都是2的整数倍。

Introduction

goal of this paper:

利用金字塔结构来创造一个在所有尺度都有很强的语义信息的特征金字塔。

how to achieve：

通过自顶向下的上采样和横向连接来结合低分辨率语义强的feature和高分辨率语义信息弱的features。

result：

特征金字塔的所有层的语义信息都很强，在single-scale image 上build快，内存占用比图片金字塔小。

FPN特点：

predictions（object detections）are independently made on each level

Related work

略

Feature Pyramid Networks

结合RPN和Fast RCNN

输入任意大小的single-scale image，输出按比例(2倍)变大的层，这个过程独立于骨干网络，相当于挂在骨干网络上。

FPN结构：自底向上（骨干网络）+自上到下（上采样，最临近插值算法）+横向链接（相加）

临近插值算法

方法简单，处理速度快，但图片会产生锯齿状边缘

插值法放大图像的第一步都是相同的，计算新图的坐标点像素值对应原图中哪个坐标点的像素值来填充，计算公式为：

    srcX/dstX = srcWidth/dstWidth

    srcY/dstY = srcHeight/dstHeight

​ 其中，src表示旧图，dst表示新图。新图的坐标（dstX,dstY）对应于旧图的坐标（srcX,srcY）。 srcWidth/dstWidth 和 srcHeight/dstHeight 分别表示宽和高的放缩比。拿旧图塞进新图里。

除出来不是整数就四舍五入（临近），这样会导致像素变化不连续，导致锯齿产生。

骨干网络采用resnet50：

自底向上:

就是骨干网络的前向计算，缩放比2（2倍关系）

输出map大小相同就算做同一个阶段，特征金字塔取每个阶段的最后一个map。这步很自然，因为最后一个map的特征更强。

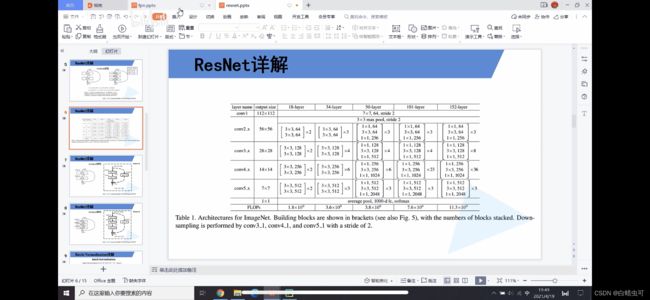
resnet50：（见上图）

We denote the output of these last residual blocks as **{C2, C3, C4, C5}**for conv2, conv3, conv4, and conv5 outputs, and note that they have strides of {4, 8, 16, 32} pixels with respect to the input image.Note：2、3、4、5自底向上。

没把第一层conv1卷积放进来，因为conv1比较大，占用内存。

自顶向下和横向连接：

自顶向下的features会通过横向链接和自底向上的feature连接获得增强，空间上相同的会连在一起。自底向上的feature map语音信息少，但其activation（？）由于下采样少会更准确。

上采样（最邻近插值算法）的倍率也是2，上采样之后，之后和对应的自底向上的map（用一个1*1卷积降维后）逐元素相加。

此过程反复迭代直到最好的resolution map生成完。

迭代开始，在C5上用1* 1卷积。最终用3* 3卷积在每个相加的map上再去生成最终的feature map （减小上采样的aliasing effect）。

混叠（英语：Aliasing），频率名词，在信号频谱上可称作叠频；在影像上可称作叠影。主要来自于对连续时间信号作取样以数字化时，取样频率低于两倍奈奎斯特频率。

在统计、信号处理和相关领域中，混叠是指取样信号被还原成连续信号时产生彼此交叠而失真的现象。当混叠发生时，原始信号无法从取样信号还原。而混叠可能发生在时域上，称做时间混叠，或是发生在频域上，被称作空间混叠。
在视觉影像的模拟数字转换或音乐信号领域，混叠都是相当重要的议题。因为在做模拟-数字转换时若取样频率选取不当将造成高频信号和低频信号混叠在一起，因此无法完美地重建出原始的信号。为了避免此情形发生，取样前必须先做滤波的操作。

This final set of feature maps is called {P2, P3, P4, P5}, corresponding to {C2, C3, C4, C5}that are respectively of the same spatial sizes.

由于金字塔和传统的图片金字塔一样分类器/回归器共享，所有额外的卷积（？）的feature map的feature维度固定为256。影响不大。

应用

做了小的调整

head：在3* 3卷积层后连接的两个并列的1* 1卷积，分类器和回归器

RPN

将single-scale feature map（图1b） 换成FPN。金字塔的每层都连接一个和faster rcnn一样的分类器和回归器（head）。

每层anchor的大小是固定的Formally, we define the anchors to have areas of {32^2, 64^2, 128^2, 256^2, 512^2} pixels on {P2, P3, P4, P5, P6} respectively.这里的P6是P5步长为2的下采样，在Fast rcnn中不用P6，只是在RPN中使用，获得的窗口根据公式送进Fast RCNN 中对应的层（下面会讲）2~5。

P6引入是为了能让anchor覆盖512^2大小。RPN的滑动窗在每层都有。

We also use anchors of multiple aspect ratios {1:2, 1:1, 2:1} at each level. So in total there are 15 anchors over the pyramid.

给anchor分配正负标签和faster rcnn一样，IoU（Intersection-over-Union ratios）高于0.7就正样本（好像忽略了第二种情况），低于0.3就作负样本，其他的丢掉。

head的参数在所有层中都共享（和不共享的差不多）。

Feature Pyramid Networks for Fast R-CNN

将RPN给出的候选框分配到不同层 （Pk）进行RoI pooling：

we assign an RoI of width w and height h(on the input image to the network) to the level Pk of our feature pyramid by:
$$k=\lfloor k_0+{\log }_2(\sqrt{wh}/224)\rfloor .$$
Here 224 is the canonical（classic）ImageNet pre-training size, and k0 is the target level on which an RoI with w × h = 224^2should be mapped into. Analogous to the ResNet-based Faster R-CNN system [16] that uses C4 as the single-scale feature map, we set k0 to 4. Intuitively, Eqn. (1) means that if the RoI’s scale becomes smaller (say, 1/2 of 224), it should be mapped into a finer-resolution level (say, k = 3).

pytorch里可以用levelmapper函数实现分配层级。

We attach predictor heads (in Fast R-CNN the heads are class-specific classifiers and bounding box regressors) to all RoIs of all levels. heads都共享参数。和fast rcnn不同，论文ROI pooling 缩放成7*7大小的features之后，再连上两个fc层（ReLu）之后才连上最后的分类和回归器。这些层都随机初始化，在resnet中找不到预训练的fc层。（比之前的快）

实验证明（目标检测）

采用了消融实验。

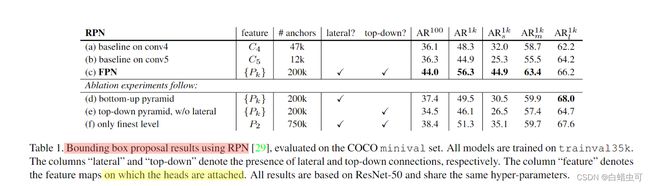
由表1可知FPN中的自下到上，自上到下，还有横向链接都是十分重要的。AR是平均召回率（真阳性的数量除以真阳性和假阴性的总和）

a的结果比b好表明 2-fc head does not give us any orthogonal advantage over

表2固定候选框，可见FPN确实会提升效果

表3是相同backbone和baseline之间的对比，FPN更强。

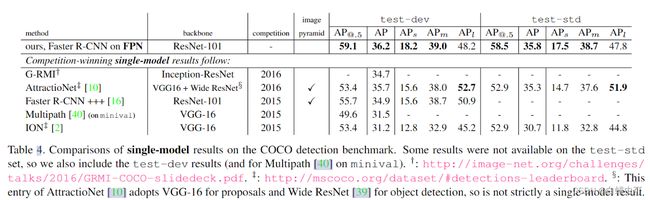
表4是FPN和其他几个single-model之间的对比。FPN高的多。

总结

语义分割没怎么读。
FPN确实可以提高feature map的语义信息，可以参考这种金字塔结构，或者改变分类器回归器可能有更好的结果。