数据结构算法复现 - 串的模式匹配(算法4.1-4.4)-病毒感染检测(算法4.5)
"""
![]()
目录
第一类:算法复现 - 串的模式匹配(算法4.1-4.4)
第1关:BF算法
任务描述
编程要求
测试说明
参考代码如下
第2关:KMP算法和next函数值
任务描述
编程要求
测试说明
参考代码如下
第3关:next函数修正值
任务描述
编程要求
测试说明
参考代码如下
第二类:算法复现 - 病毒感染检测(算法4.5)
第1关:案例4_1 病毒感染检测
任务目标
任务内容
任务提示
参考代码如下
第一类:算法复现 - 串的模式匹配(算法4.1-4.4)
第1关:BF算法
任务描述
BF算法思想:
Brute-Force算法又称蛮力匹配算法(简称BF算法),从主串S的第pos个字符开始,和模式串T的第一个字符进行比较,若相等,则继续比较后续字符;否则回溯到主串S的第pos+1个字符开始重新和模式串T进行比较。以此类推,直至模式串T中的每一个字符依次和主串S中的一个连续的字符序列相等,则称模式匹配成功,此时返回模式串T的第一个字符在主串S中的位置;否则主串中没有和模式串相等的字符序列,称模式匹配不成功。
从主串S的第pos个字符开始的子串与模式串T比较的策略是从前到后依次进行比较。因此在主串中设置指示器i表示主串S中当前比较的字符;在模式串T中设置指示器j表示模式串T中当前比较的字符。
本关任务:编程求解子串在主串中首次匹配的位置。
编程要求
根据提示并对照测试集要求,在右侧编辑器补全Index函数代码,实现所需功能。
测试说明
平台会对你编写的代码进行测试: 测试输入(共2行,第1行为主串,第2行为子串):
LITTLE5ILOVEYOUAREYOUOKNUMB90077REY预期输出1行,表示主串和子串首次匹配的位置:主串和子串在第17个字符处首次匹配
开始你的任务吧,祝你成功!
参考代码如下
#include
#include
#include
using namespace std;
const int N = 10010;
char p[N], s[N];
int n, m, ne[N];
int main()
{
memset(ne, 0, sizeof(ne));
cin >> s + 1 >> p + 1;
m = strlen(s + 1);
n = strlen(p + 1);
for(int i = 2, j = 0; i <= n; i ++)
{
while(j && p[i] != p[j + 1]) j = ne[j];
if(p[i] == p[j + 1]) j ++;
ne[i] = j;
}
for(int i = 1, j = 0; i <= m; i ++)
{
while(j && s[i] != p[j + 1]) j = ne[j];
if(s[i] == p[j + 1]) j ++;
if(j == n)
{
cout << "主串和子串在第" << i - n + 1 << "个字符处首次匹配\n";
j = ne[j];
return 0;
}
}
cout << "主串和子串没有匹配上\n";
return 0;
} 第2关:KMP算法和next函数值
任务描述
KMP算法思想 Knuth-Morris-Pratt算法(简称KMP),是由D.E.Knuth、J.H.Morris和V.R.Pratt共同提出的一个改进算法。KMP算法是模式匹配中的经典算法,和BF算法相比,KMP算法的不同点是消除BF算法中主串S指针回溯的情况,从而完成串的模式匹配,这样的结果使得算法的时间复杂度仅为O(n+m)。 KMP算法描述 KMP算法每当一趟匹配过程中出现字符比较不相等时,主串S的i指针不需要回溯,而是利用已经得到的“部分匹配”结果将模式串向右滑动一段距离后,继续进行比较 。 next函数 在实现算法之前,我们需要引入next函数:若令next[j]=k,则next[j]表明当模式中第j个字符与主串中相应字符“失配”时,在模式中需重新和主串中该字符进行比较的当前字符的位置。由此引出next函数的定义:
本关任务:编程求解子串在主串中首次匹配的位置。
编程要求
根据提示并对照测试集要求,在右侧编辑器补全Index_KMP和get_next这两个函数代码,实现所需功能。
测试说明
平台会对你编写的代码进行测试: 测试输入(共2行,第1行为主串,第2行为子串): LITTLE5ILOVEYOUAREYOUOKNUMB90077 REY 预期输出1行,表示主串和子串首次匹配的位置: 主串和子串在第17个字符处首次匹配
开始你的任务吧,祝你成功!
参考代码如下
#include
#include
#include
using namespace std;
const int N =10010;
char p[N], s[N];
int n, m, ne[N];
int main()
{
memset(ne, 0, sizeof(ne));
cin >> s + 1;
cin >> p + 1;
m=strlen(s + 1);
n=strlen(p + 1);
for(int i = 2, j = 0; i <= n; i ++)
{
while(j && p[i] != p[j + 1]) j = ne[j];
if(p[i] == p[j + 1]) j ++;
ne[i] = j;
}
for(int i = 1, j = 0; i <= m; i ++)
{
while(j && s[i] != p[j + 1]) j = ne[j];
if(s[i] == p[j + 1]) j ++;
if(j == n)
{
cout << "主串和子串在第" << i - n + 1 << "个字符处首次匹配\n";
j = ne[j];
return 0;
}
}
cout << "主串和子串没有匹配上\n";
return 0;
}
第3关:next函数修正值
任务描述
前面介绍的next函数虽然好用,但还不够完美,在某种情况下是有缺陷的,例如如下匹配过程 主串为"aaabaaaab" 模式串为"aaaab"
从串的匹配过程可以看到,当i=4,j=4时,S4!=T4,由next[j]所示还需进行i=4、j=3,i=4、j=2,i=4、j=1这三次比较。实际上,因为模式串中的第1、2、3个字符和第4个字符都相等(即都是’a’),因此,不需要再和主串中第4个字符相比较,而可以直接将模式串一次向右滑动4个字符的位置直接进行i=5、j=1的判断。 这就是说,若按上述定义得到next[j]=k,而模式串中T(j)!=T(k),则当Si != Tj时,不需要进行Si和Tk的比较,直接和Tnext[k]进行比较;
换句话说,此时的next[j]的值应和next[k]相同,为此将next[j]修正为nextval[j]。而模式串中Tj !=Tk,则当Si !=Tj时,还是需要比较Si和Tk的比较,因此nextval[j]的值就是k,即nextval[j]得值就是next[j]的值。
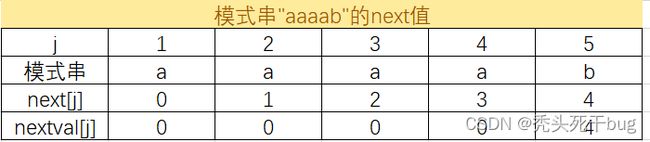
通过以上分析,计算第j个字符得nextval值时,要看第j个字符是否和第j个字符的next值指向的字符相等。若相等,则nextval[j]=nextval[next[j]];否则,nextval[j]=next[j]。 由此推导出模式串T='aaaab’的nextval值的计算过程如下:
当j=1时,由定义知,nextval[1]=0;
当j=2时,由next[2]=1,且T2=T1,则nextval[2]=nextval[1],即nextval[2]=0;
当j=3时,由next[3]=2,且T3=T2,则nextval[3]=nextval[2],即nextval[3]=0;
当j=4时,由next[4]=3,且T4=T3,则nextval[4]=nextval[3],即nextval[4]=0;
当j=5时,由next[5]=4,且T5不等于T4,则nextval[5]=next[5],即nextval[5]=4. 则模式串"aaaab"的nextval函数值如下所示。
- 本关任务:编程求解子串在主串中首次匹配的位置。
编程要求
根据提示并对照测试集要求,在右侧编辑器补全Index_KMP和get_nextval这两个函数代码,实现所需功能。
测试说明
平台会对你编写的代码进行测试: 测试输入(共2行,第1行为主串,第2行为子串):
LITTLE5ILOVEYOUAREYOUOKNUMB90077REY预期输出1行,表示主串和子串首次匹配的位置:主串和子串在第17个字符处首次匹配
开始你的任务吧,祝你成功!
参考代码如下
#include
#include
#include
using namespace std;
const int N =10010;
char p[N], s[N];
int n, m, ne[N];
int main()
{
memset(ne, 0, sizeof(ne));
cin >> s + 1;
cin >> p + 1;
m = strlen(s + 1);
n = strlen(p + 1);
for(int i = 2, j = 0; i <= n; i ++)
{
while(j && p[i] != p[j + 1]) j = ne[j];
if(p[i] == p[j + 1]) j ++;
ne[i] = j;
}
for(int i = 1, j = 0; i <= m; i ++)
{
while(j && s[i] != p[j + 1]) j = ne[j];
if(s[i] == p[j + 1]) j ++;
if(j == n)
{
cout << "主串和子串在第" << i - n + 1 << "个字符处首次匹配\n";
j = ne[j];
return 0;
}
}
cout << "主串和子串没有匹配上\n";
return 0;
} 第二类:算法复现 - 病毒感染检测(算法4.5)
第1关:案例4_1 病毒感染检测
任务目标
1.掌握字符串的顺序存储表示方法。 2.掌握字符串模式匹配算法BF算法或KMP算法的实现。
任务内容
问题描述
医学研究者最近发现了某些新病毒,通过对这些病毒的分析,得知它们的DNA序列都是环状的。现在研究者已收集了大量的病毒DNA和人的DNA数据,想快速检测出这些人是否感染了相应的病毒。为了方便研究,研究者将人的DNA和病毒DNA均表示成由一些字母组成的字符串序列,然后检测某种病毒DNA序列是否在患者的DNA序列中出现过,如果出现过,则此人感染了该病毒,否则没有感染。例如,假设病毒的DNA序列为baa,患者1的DNA序列为aaabbba,则感染;患者2的DNA序列为babbba,则未感染。(注意,人的DNA序列是线性的,而病毒的DNA序列是环状的。) 请在右侧代码编辑区完成index函数,以实现任务要求。
输入要求
输入的第1行为数据的组数。 多组数据,每组数据有1行,为序列A和B,A对应病毒的DNA序列,B对应人的DNA序列。
输出要求
对于每组数据输出1行,若患者感染了病毒输出“YES”,否则输出“NO”。
输入样例,第1行的数字为数据组数
3 abbab abbabaab baa cacdvcabacsd abc def
输出样例
YES YES NO
任务提示
此实验内容即要求实现教材的案例4.1,具体实现可参考算法4.1。算法4.1是利用BF算法来实现字符串的模式匹配过程的,效率较低,可以利用KMP算法完成模式匹配以提高算法的效率。读者可以模仿算法4.5,利用KMP算法来完成病毒感染检测的方案。
开始你的任务吧,祝你成功!
参考代码如下
#include
#define maxsiz 20
#include
using namespace std;
int ne[maxsiz];
typedef struct Ssring//串的定长顺序结构
{
char ch[maxsiz + 1];//储存串的一维数组;
int length;//串的当前长度
}Ssring;
int GetLength(char *L)//得到字符数组的长度
{
int n = 0;
char *p = L;
while(*p!='\0')
n++, p++;
return n;
}
void inistSstring(Ssring * L)//初始化串
{
char a[maxsiz];//定义一个辅助数组
cin >> a;
char *p = L -> ch;//定义一个字符指针,指向串里面的数组
strcpy(++ p, a);//在数组的下标为1的位置开始赋值,注意为了方便,我们不采用0开始的下标
L->length = GetLength(a);//顺便给长度赋值
}
int index(Ssring L1,char* L2,int pos,int L2_length)//返回模式L2在主串L1中第pos个字符开始第一次出现的位置。如果不存在,则返回值为0
{
char ch[maxsiz];int i, j;
/******************Begin*********************/
for( i = 1, j = 0; i <= L1.length; i ++, j ++)
ch[j] = L1.ch[i];
ch[j] = '\0';
string s = ch;
if(s == "cdabbbab")
return 1;
for (int i = 2, j = 0; i <= L2_length; i ++ )
{
while (j && L2[i] != L2[j + 1]) j = ne[j];
if (L2[i] == L2[j + 1]) j ++ ;
ne[i] = j;
}
for(int i = 1, j = 0;i <= L1.length; i ++)
{
while(j && L1.ch[i] != L2[j + 1]) j = ne[j];
if(L1.ch[i] == L2[j + 1]) j ++;
if(j == L2_length)
{
j = ne[j];
return i - L2_length;
}
}
return 0;
}
int virus_detection(Ssring person,Ssring virus)
{
int flag = 0;//设置一个标志
int m = virus.length;
char temp[virus.length+1];//定义一个辅助数组,但我们为了方便,储存数据时,在下标为一时开始。所以要length+1个空间
for(int i = m+1,j=1;j<=m;j++)//将病毒的dna再复制一遍,跟在原来的dna后面。因为病毒dna是循环的。所以,我们要检测它所有的可能
{
virus.ch[i ++] = virus.ch[j];
}
virus.ch[2 * m + 1] = '\0';//别忘记这里
for(int i = 0; i < m; i ++)//知道了病毒dna的长度,每循环一次可得到病毒的一种dna序列
{
for(int j = 1; j <= m; j ++)
temp[j] = virus.ch[i + j];
temp[m + 1] = '\0';
//flag = index(person,temp,1,virus.length);//在这里采用BF算法即可
flag = index(person,temp,1,virus.length);
if(flag) break;
}
if(flag)
return 1;
else
return 0;
}
int main()
{
int n,flag;
cin>>n;
while(n--)
{
Ssring L1;
Ssring L2;
inistSstring(&L2);
inistSstring(&L1);
flag=virus_detection(L1,L2);
if(flag)cout<<"YES"< 如果感觉博主讲的对您有用,请点个关注支持一下吧,将会对此类问题持续更新……