Gumbel softmax trick pytorch（快速理解附代码）

也可查看我的知乎: Gumbel softmax trick （快速理解附代码）

（一）目的

在深度学习中，对某一个离散随机变量$X$进行采样，并且又要保证采样过程是可导的（因为要用梯度下降进行优化，并且用BP进行权重更新），那么就可以用Gumbel softmax trick。属于重参数技巧(re-parameterization)的一种。

首先我们要介绍，什么是Gumbel distribution，然后再介绍怎么用到梯度下降中，最后用pytorch实现它。

（二）什么是Gumbel distribution？

一种极值分布（或者叫做Fisher-Tippett extreme value distributions），顾名思义就是用来研究极值（极大值，或者极小值）的一种概率分布形式。和别的一些分布形式一样，给定一个描述分布的公式，然后再给定公式中的某些参数，那么就确定了这个分布。

（本质就是想用数学语言或公式来逼近或解释现实世界观察到的现象，比如自然界很多现象可以用正太分布来描述，自然地，也存在一些自然现象，要用极值分布来描述。）

举个简单的例子： 某高中三年级一共有16个班，现在从每个班级里面抽出30人（假设全为男生或者全为女生），那么现在总共有16组30人的样本。如果看每组样本里面的身高分布大概率是服从正态分布的。现在，从每组样本里面挑出身高最高的人，将这些人再组成一个新样本集合，也就是现在这个样本集合有16个人，那么这16个人的样本集合就是服从的Gumbel 分布（极大值 Gumbel distribution，当然也有极小值 Gumbel distribution）。

下面定义极大值的Gumbel distribution。

CDF:

$$F(x;\mu ,\beta )=e^{-e^{-\frac{(x-\mu )}{\beta }}}$$

PDF:

$$f(x)=\frac{\partial F}{\partial x}=\frac{1}{\beta }{e}^{-(z+e^{-z})},$$
where $z=\frac{x-\mu }{\beta }$.

标准Gumbel 分布：

即，$\mu =0,\beta =1$, 则CDF为：
$$F(x;\mu =0,\beta =1)=F(x)=e^{-e^{-(x)}}$$

函数图像：

（三）什么是Gumbel softmax trick？

Gumbel分布描述了自然界或者说人造的某种数据（其实也是自然界吧，毕竟人也是自然的一部分。）的极值分布的 “规律”（分布其实只是认识”规律“的一种方式）。所以自然地，我们之所以会用到Gumbel分布，就是因为我们要处理的数据中，存在极值分布（~废话）。

考虑如下场景：

对一个离散随机变量$\mathbf{X}$进行采样，随机变量的取值范围为$\{1,2,...,K\}$。首先要知道随机变量的分布函数，这里假设用MLP学习一个K维的向量：$\mathbf{h}\in {\mathbb{R}}^K$。

（假如是直接做inference的话，不考虑概率意义，那么我们直接取这个向量元素最大值的下标当做预测的离散变量值就可以了，即，$X_i=\arg {\max }_i{h}_i$.，但我们希望的是预测的离散变量具有概率意义，或者说得到的多个预测值的经验分布符合理论的概率分布。否则的话就是deterministic的，会导致某些小概率的变量值根本取不到，进而影响后续的任务。）

所以，我们需要赋予概率意义。通常，我们可以用softmax函数作用到$\mathbf{h}$求得一个符合概率意义的新概率向量，即：
$$p_i=softmax(h,h_i)=\frac{exp(h_i)}{{\sum }_{i}exp(h_i)}.$$
这样我们就获得了各个离散取值的概率分布$\mathbf{p}\in [0,1{]}^K$，其中$p_i=Pr\{X_i=i\}$。这里$\mathbf{p}$是一个在K维simplex中的一个向量。

到这里，我们得到了$X$的概率分布，如果要直接得到离散变量，直接取$X_i=\arg {\max }_i{p}_i$即可。（注意，这里每次inference的时候，取了最大值，是不是和Gumbel分布的含义很像了。）

问题是我们需要的是采样，也就是生成的多个样本的频率分布要符合其理论的概率分布。另外，可以开始考虑，是否能够将求导和采样这两个操作解耦。

如果知道一些reparameterization trick的技巧，很容易想到，我们只需要将$\mathbf{p}$加上一个要学习的参数无关（即无需进行求导）的某个随机变量$\mathbf{g}$，那么采样过程就可以通过$\mathbf{g}$进行（曲线救国了算是），这样做相当于把求导与采样解耦了。这里，只需要保证结合后的分布，与原分布$\mathbf{p}$相等或近似即可。

接下来就是与服从Gumbel分布的随机变量$\mathbf{g}$结合：

$$X_i=\arg \underset{i}{\max }(\log (p_i)+g_i)$$
这里$g_i$是一个提前采样好的标准Gumbel分布序列。通过这种方法，理论上可以证明，这个新随机变量的分布函数和原分布函数相等。证明见：。。

但这样的问题在于$\arg \max ()$不可导，导致无法使用梯度下降来更新参数。所以一种办法是将随机变量的取值从$1,...,K$变为用一个K维的one_hot向量编码来表示。比如，本来取$X_i=i$，现如果用one_hot来表示的话，就是$X_i=(0,...,1,...,0)$，也就是第$i$个下标的值为1，其它都为0，我们记第$i$个下标的值为$y_i$。那么我们就可以用softmax函数来近似这个one_hot向量：

$$y_i=\frac{\exp ((\log (p_i)+g_i)/\tau )}{{\sum }_{k=1}^K\exp ((\log (p_k)+g_k)/\tau )}$$
这里的$\tau$被叫做温度系数，或者说是一个缩放因子。一般来说，$\tau <1$，想象一下以$e$为底的指数分布图像，可以发现，如果$\tau$越小，指数的值$e^{(x/\tau )}越大，简记x=log(p_i)+g_i$。也就是说，这个$\tau$存在的意义就是让本来大的$x$越大，所以会导致$y_i$越接近1，并且$\forall j\ne i,y_j$会接近0，所以$X_i$就更接近一个one_hot表示。
图片来源于文章[7]: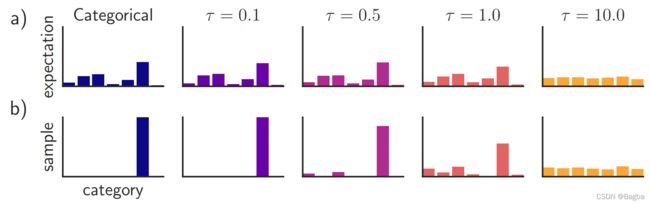

（四）如何生成Gumbel分布的样本

最后一步，就是如何生成Gumbel 分布的样本，即，如何产生$g_i$。

这里使用最常见的一种方法也就是inverse CDF method。先求出Gumbel的CDF函数$F(x;\mu ,\beta )$的反函数$x=F^{-1}(y;\mu ,\beta )=\mu -\beta \ln (-\ln y)$（根据CDF的公式：$y=F(x;\mu ,\beta )$，把y和x反过来表示就可），然后只要生成$y\sim Uniform(0,1)$的均匀分布的序列，那么相应的$x$就服从Gumbel分布，$x\sim Gumbel(\mu ,\beta )$，也即，$x$的CDF函数为原来的$F(x)$。证明如下：
$$P(F^{-1}(y)\le x)=P(y\le F(x))={\int }_0^{F(x)}pdf(y)dy={\int }_0^{F(x)}1dy=F(x)$$

---

到这里我们就可以通过以上的公式进行采样了。

（五）pytorch实现

下面用pytorch实现一下上面描述的采样过程。

# Gumbel softmax trick:

import torch
import torch.nn.functional as F
import numpy as np

def inverse_gumbel_cdf(y, mu, beta):
    return mu - beta * np.log(-np.log(y))

def gumbel_softmax_sampling(h, mu=0, beta=1, tau=0.1):
    """
    h : (N x K) tensor. Assume we need to sample a NxK tensor, each row is an independent r.v.
    """
    shape_h = h.shape
    p = F.softmax(h, dim=1)
    y = torch.rand(shape_h) + 1e-25  # ensure all y is positive.
    g = inverse_gumbel_cdf(y, mu, beta)
    x = torch.log(p) + g  # samples follow Gumbel distribution.
    # using softmax to generate one_hot vector:
    x = x/tau
    x = F.softmax(x, dim=1)  # now, the x approximates a one_hot vector.
    return x

N = 10  # 假设 有N个独立的离散变量需要采样
K = 3   # 假设 每个离散变量有3个取值
h = torch.rand((N, K))  # 假设 h是由一个神经网络输出的tensor。

mu = 0
beta = 1
tau = 0.1

samples = gumbel_softmax_sampling(h, mu, beta, tau)

References

1. https://mathworld.wolfram.com/GumbelDistribution.html
2. https://www.itl.nist.gov/div898/handbook/eda/section3/eda366g.htm
3. https://en.wikipedia.org/wiki/Fisher%E2%80%93Tippett%E2%80%93Gnedenko_theorem
4. https://en.wikipedia.org/wiki/Gumbel_distribution
5. https://www.cnblogs.com/initial-h/p/9468974.html
6. https://arxiv.org/pdf/1611.04051.pdf
7. https://arxiv.org/abs/1611.01144